Корреляционные и спектральные характеристики случайных процессов

Инерционность в динамических системах характеризуется значениями корреляционных связей 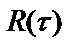между временными сечениями процесса 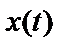, отстоящими на интервал 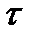. Широкая разновидность процессов 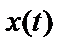обладает корреляционными функциями вида:

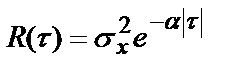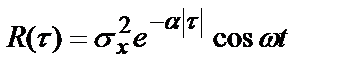; . (5.20)

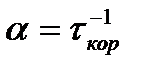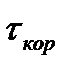Параметр , где - интервал корреляции, на котором значение 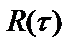уменьшается на 0,37. Корреляционные функции (5.20) используют в теории, технологиях и на практике телекоммуникаций. Так с интервалами корреляции 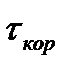сопоставляют интервалы прогноза (экстраполяции) состояний сетевых элементов в том смысле, что время прогноза 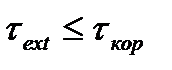, при этом, чем меньше 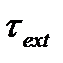по сравнению с 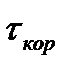, тем точнее прогноз. Зависимость или независимость отсчетов выборки находятся исходя из сопоставления интервалов этих отсчетов 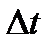с 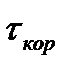. Так при 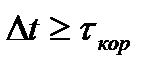- отсчеты независимы, при 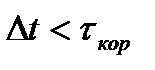- зависимы. Кроме того, в системах управления от инерционности контура управления 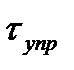зависит эффективность задачи управления в том смысле, что будет ли успевать система управления «отрабатывать» задачу или только частично.

Нормированная корреляционная функция:

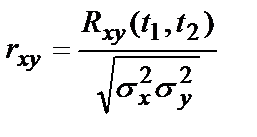
Для расчетных задач по дискретной выборке 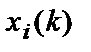и 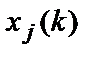используется формула:

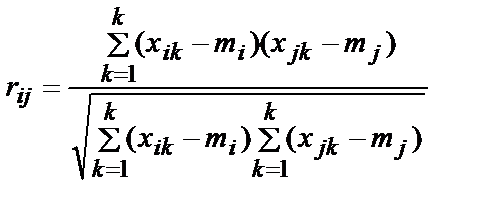. (5.21)

Корреляционная функция 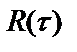связана парой преобразований Фурье со спектральной плотностью мощности (СПМ) стационарного случайного процесса:

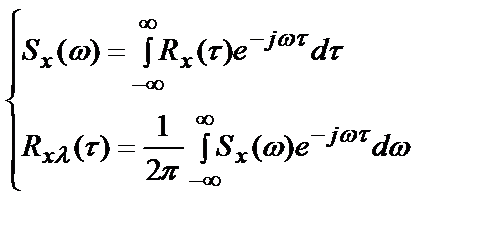(5.22)

Соотношения (5.22) носят название формул Винера-Хинчина.

СПМ 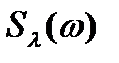позволяет проводить анализ процессов по их частотным характеристикам. Так, выбирая генератор гауссового белого шума (ГБШ) стремятся, чтобы СПМ была как можно более равномерной, без заметных провалов на оси частот, по ширине спектра выбирают требуемую полосу частот для передачи информационного потока, и др.

Рассмотрим ряд задач по анализу временных и частотных характеристик случайных процессов.

Задача 5.1. Выяснить разницу между спектральными плотностями стационарных случайных процессов 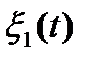и 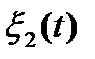с нулевыми математическими ожиданиями и корреляционными функциями

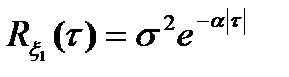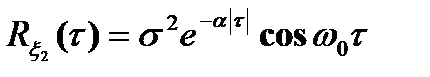, . (5.23)

Решение. Корреляционная функция 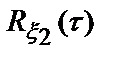является частным случаем корреляционной функции 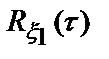. Поэтому вначале найдем спектральную плотность 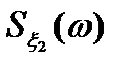, соответствующую 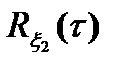, а затем из 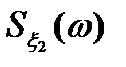получим .

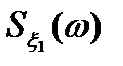Согласно формулам Винера-Хинчина имеем

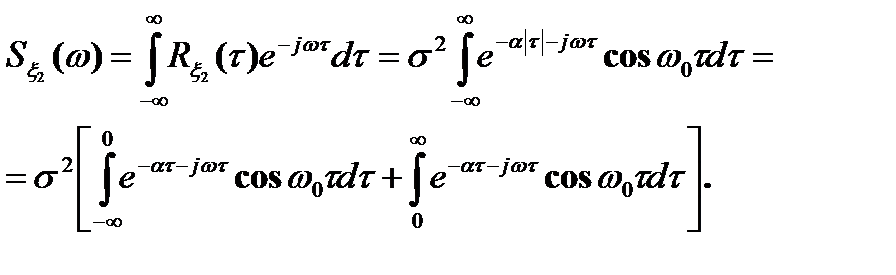
Учитывая, что

,

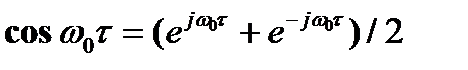получаем

.

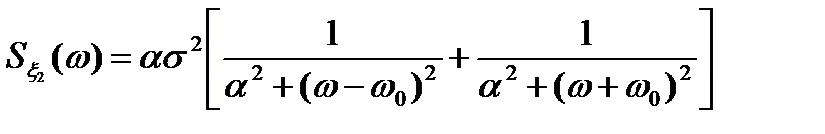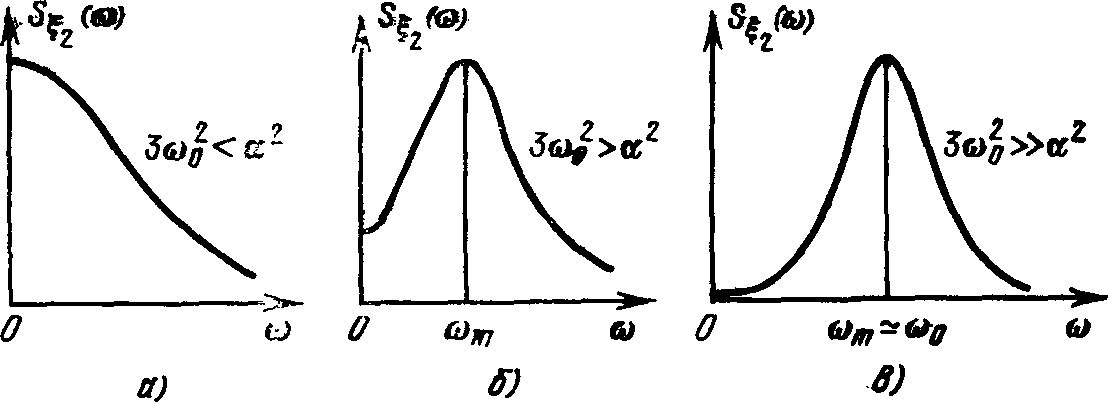
Рис.5.5. Спектральные плотности при различных соотношениях между и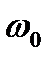

Рассмотрим поведение функции .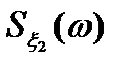

1. 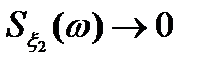при .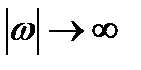

2. При 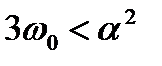у функции 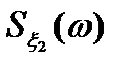нет максимума, она монотонно убывает с ростом 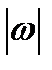(рис.5.5,а).

3. Если 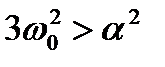, функция 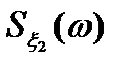имеет максимум (рис. 5.5,б) в точке

.

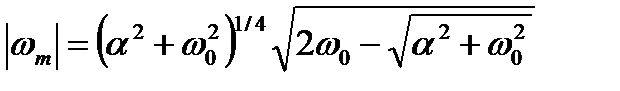4. При 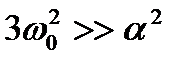спектральная плотность 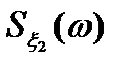также имеет максимум в точке 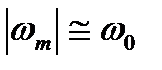(рис. 5.5,в).

Суммирование спектральных плотностей 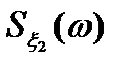с различными весами при соответствующим образом выбранных 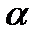и 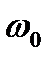позволяет аппроксимировать спектральные плотности сложных процессов. Так, к примеру, путем сложения изображенных на рис. 5.5 функций 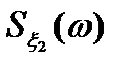можно получить спектральные плотност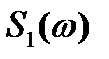и и 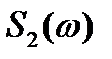(рис.5.6), хорошо совпадающие с экспериментально определенными спектральными плотностями случайных изменений во времени скоростей в атмосферном турбулентном потоке.

Полагая в 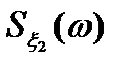частоту 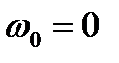, находим спектральную плотность 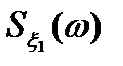, соответствующую корреляционной функции :

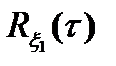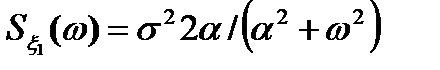. (5.24)

Графики функци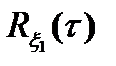и и 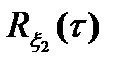и соответствующих им спектральных плотносте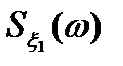й и 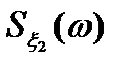приведены на рис.5.7.

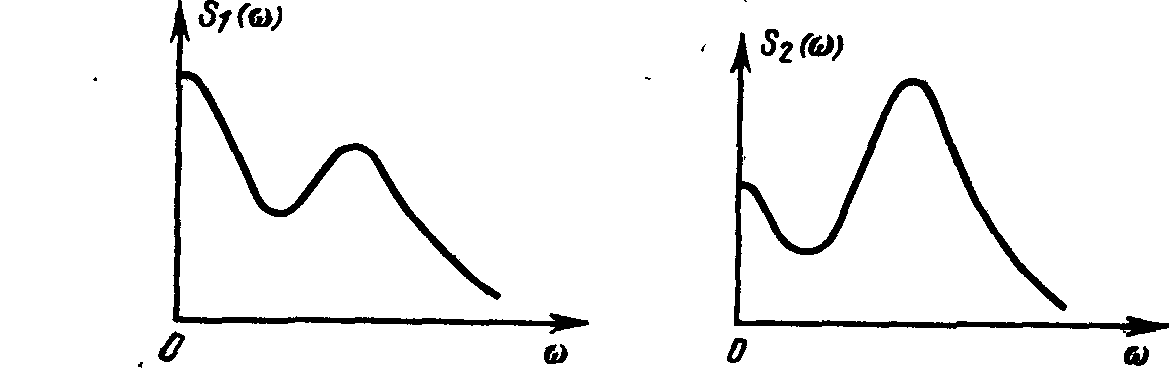
Рис.5.6. Сложные спектральные плотности

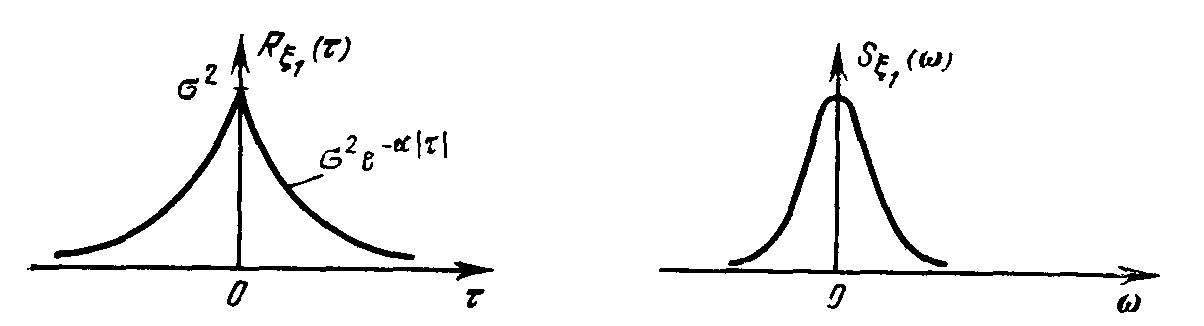
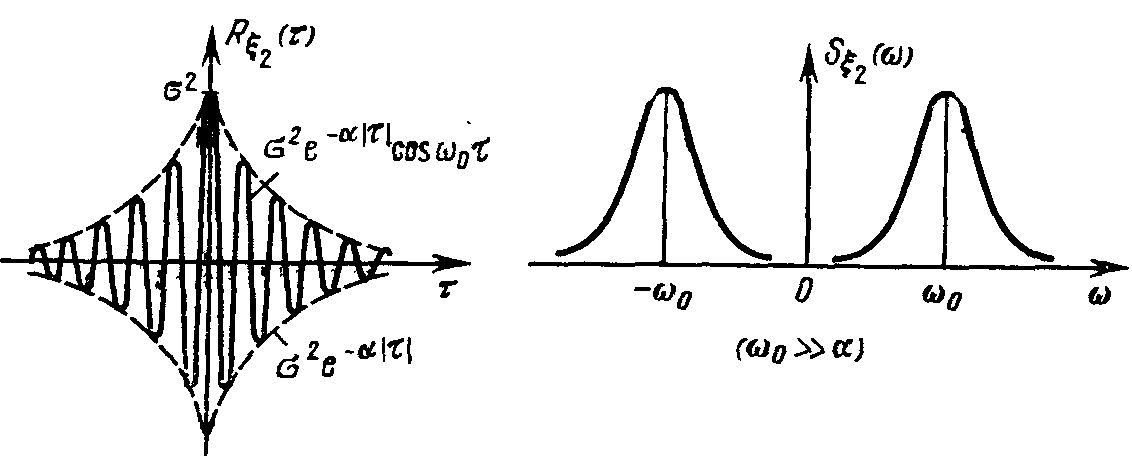
Рис.5.7. Корреляционные функции и соответствующие им спектральные плотности

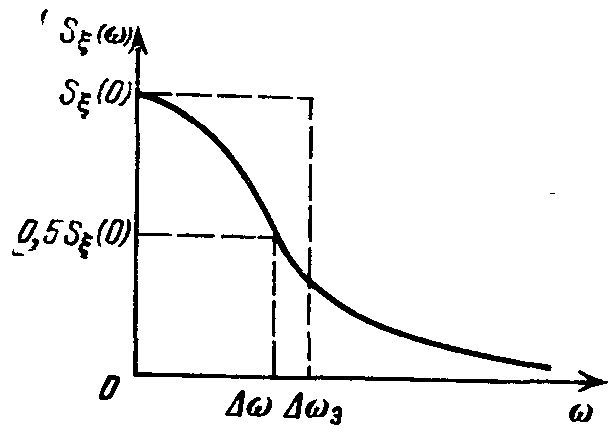
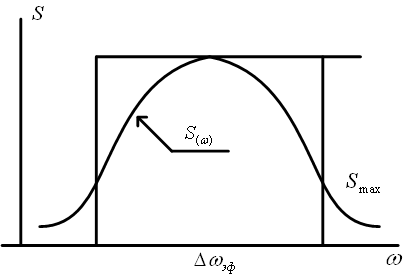
Задача 5.2.Определить эффективную ширину спектра стационарного случайного сигнала

а	б

в

Рис.5.8. Пояснение к понятиям эффективной полосы частот а и интервала корреляции б

Односторонняя спектральная плотность 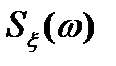стационарного случайного процесса имеет вид (рис.5.5 а)

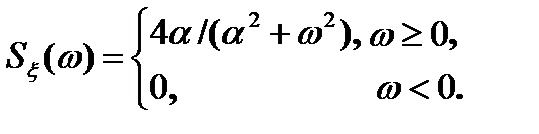
Для двухсторонней СПМ 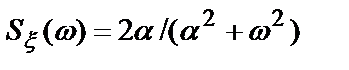, для .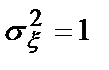

Необходимо определить соотношение между эффективной шириной спектра 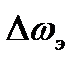процесса 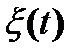и шириной его спектральной плотности 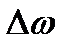на уровне .

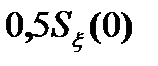Решение. Эффективная ширина спектра 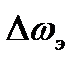процесса 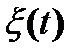определяется как площадь равновеликого СПМ прямоугольника, высота которого равна 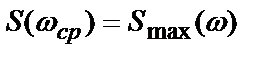(рис.5.5 б):

.

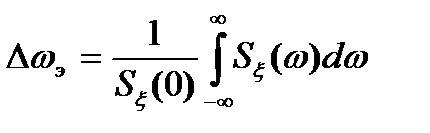В предположении 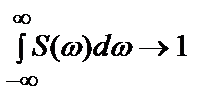, после подстановки 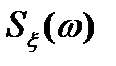находим

.

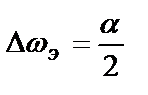Следовательно, с учетом 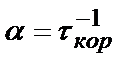получаем 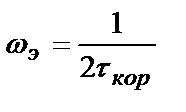или .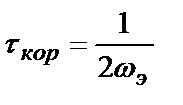

Задача 5.3.

Найти интервал корреляции 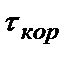для стационарных случайных процессов 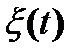с корреляционными функциями:

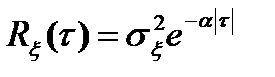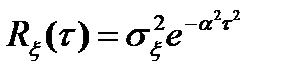1) ; 2) ; 3) , .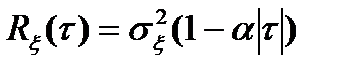

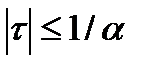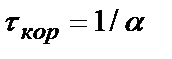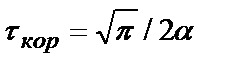Ответ: 1) ; 2) ; 3) .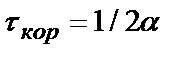

Задача 5.4.

Определить эффективную ширину 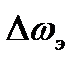спектра 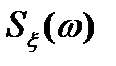стационарного случайного процесса 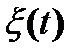с корреляционными функциями

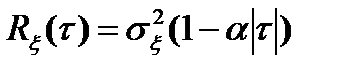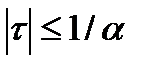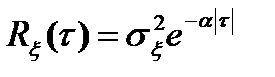1) , ; 2) ; 3) .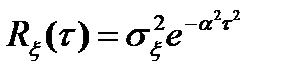

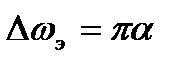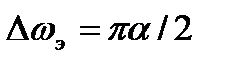Ответ: 1) ; 2) ; 3) .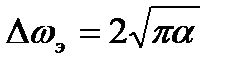

Задача 5.5.

Определить эффективную ширину спектра 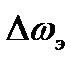, среднюю частоту спектральной плотности 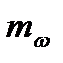, средний квадрат частоты 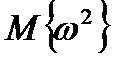и среднюю квадратическую ширину 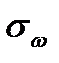спектральной плотности стационарных случайных процессов с нулевыми математическими ожиданиями и корреляционными функциями:

1) ;

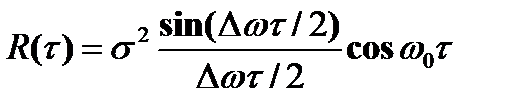2) ;

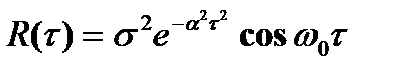3) .

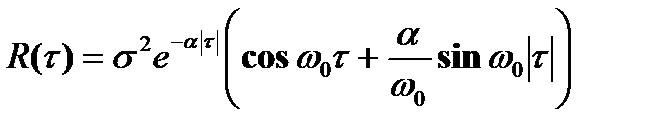Ответ:

1) , , , ;

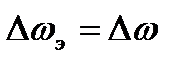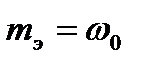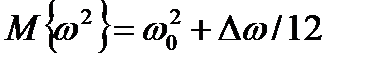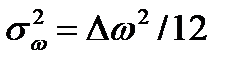2) , , , ;

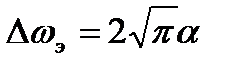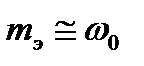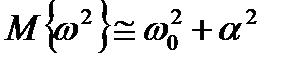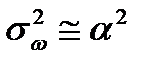3) ; , , .

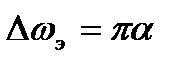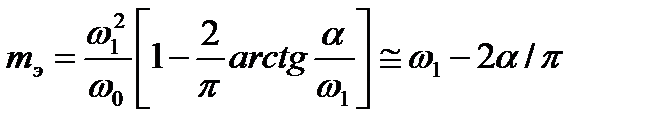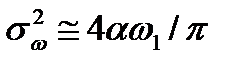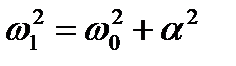Задача 5.6.

Случайный процесс 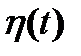получается посредством дифференцирования стационарного случайного колебания :

.

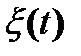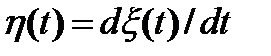Определить корреляционную функцию 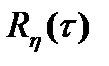процесса 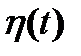в тех частных случаях, когда функция 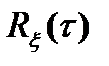колебания 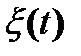задана выражениями:

1) ;

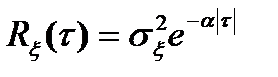2) ;

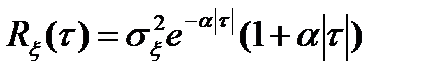3) .

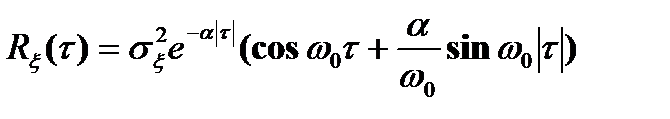Ответ.

1) ;

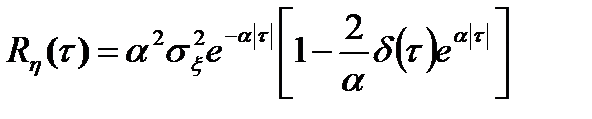2) ;

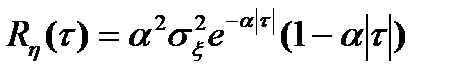3) .

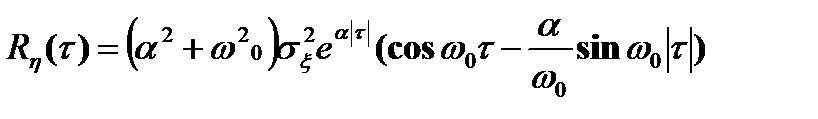5.4. Представление моделей СП Марковскими цепями

Марковские модели СП основанные на том положении, что стационарный СП (5.19) обладает известными статистическими связями между соседними сечениями: это позволяет модель условий плотности распределений записать в виде условной переходной ПРВ:

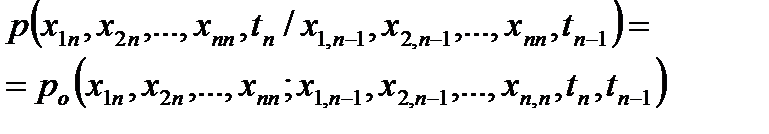(5.25)

Марковский процесс (МП) может быть 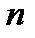-связным или МП 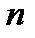-го порядка, однако наибольшую популярность приобрели односвязные процессы, у которых очередное состояние 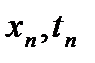зависит лишь от предыдущего состояния 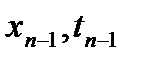(односвязные МП):

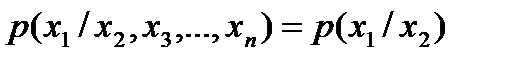, (5.26)

где 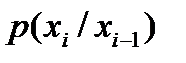- переходная ПРВ. МП считается однородным, если условия ПРВ 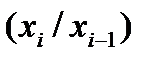не зависят от .

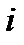Однородный МП, задаваемый с помощью переходной плотности называют цепью или Марковской цепью (МЦ).

Для однородной МЦ с начальной вероятностью 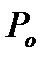и переходной вероятностью 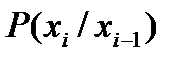можно указать возможные траектории блужданий по состояниям 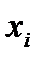(рис.5.9).

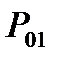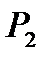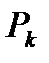, , , , где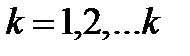

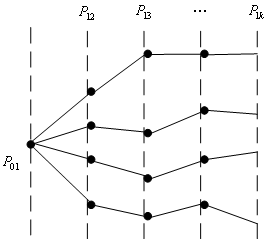
Рис. 5.9. Пример случайных блужданий МЦ при начальной вероятности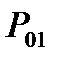

Очевидно, что при слабых статистических связях между соседними состояниями разброс траекторий возрастает, при этом возможны возвратные состояния. При отсутствии возвратных состояний МЦ называется поглощающий.

Очевидно 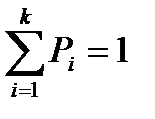, все .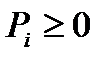

Математической моделью МЦ является матрица переходных вероятностей

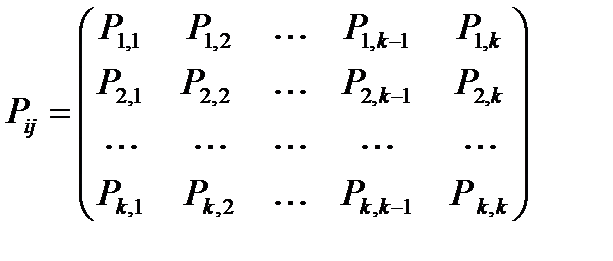(5.27)

В данной матрице строки соответствуют текущему состоянию цепи, столбцы – вероятностям состояний на очередном шаге, а на пересечении 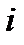-й строки и 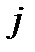-го столбца стоят вероятности 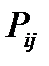соответствующего перехода.

Согласно нормировке сумма вероятностей в каждом столбце равна 1.

Возможно значения 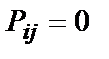, из чего следует, что такого состояния не существует, при 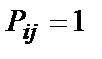обозначает, что кроме этого состоянияи, иных быть не может.

С использованием матрицы переходных вероятностей можно найти вероятность перехода МЦ из состояния 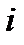в состояние 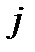ровно за 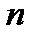шагов:

,

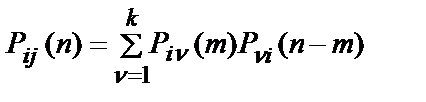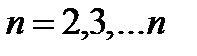
Так при 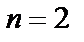получаем 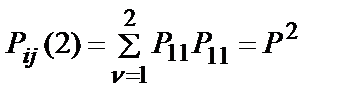. В общем случае: .

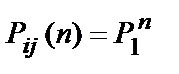Например при 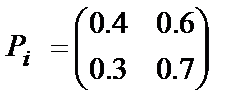получаем .

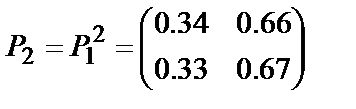Состояния МЦ называется замкнутым, если никакое состояние недостижимо ни из какого начального состояния и достижимо, если существует такое число шагов 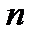, что при 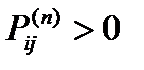МЦ переходит из состояния 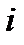в состояние .

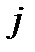Состояние МЦ называется неприводимым, если не существует замкнутых состояний. МЦ неприводима тогда, когда все ее состояния достижимы друг из друга.

Состояния МЦ бывают периодические, так при переходной матрице:

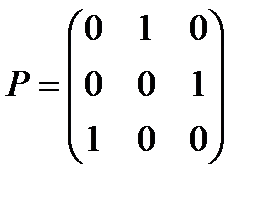
смена состояний: 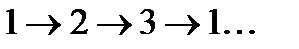с периодом 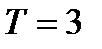. Среднее время возвращения в состояние 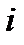(среднее число шагов возвращения ):

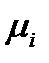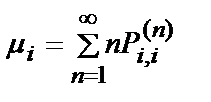, где

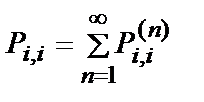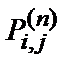, - вероятность того, что МЦ достигнет состояния 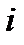, находясь в состоянии 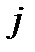, 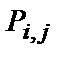- вероятность достижения состояния .

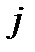МЦ называется эргодической, если она неприводима.