Базові алгоритми кластеризації
При виконанні кластеризації важливим параметром є кількість кластерів. На які треба розбити об’єкти. Вважається, що кластерізація має виявити природні локальні згущення об’єктів. Відсутність апріорно заданої кількості кластерів значно ускладнює алгоритм кластеризації і впливає на його якість. Але проблема визначення кількості кластерів є дуже не тривіальною, оскільки на початковій стадії аналізу, де використовується кластеризація, інформація о даних практична відсутня. Тому алгоритми кластерізації часто будуються у деякий спосіб перебору кількості кластерів з визначенням оптимальної їх кількості безпосередньо у процесі перебору.
Всі методи розбиття множини на кластери можна поділити на дві великі групи: ієрархічні і не ієрархічні. У не іерахічних алгоритмах характер їх роботи і умову зупинки необхідно заздалегідь регламентувати часто дуже великою кількістю параметрів, що є значною проблемою, особливо на початковому етапі вивчення даних. Але такі алгоритми є більш гнучкими з точки зору варіацій кластерізацією і зазвичай визначають кількість кластерів.
З іншого боку, коли об’єкти характеризуються великою кількістю ознак (параметрів), та важливим стає групування зв’язків. Початкова інформація міститься у квадратній матриці зв’язків ознак, зокрема, у кореляційній матриці. Основою успішного рішення задачі групування є неформальна гіпотеза про невелике кількість прихованих факторів, які визначають структуру взаємних зв’язків між ознаками.У ієрархічних алгоритмах відмовляються від визначення кількості кластерів, будуючі повне дерево вкладених кластерів (дендрограму). Кількість кластерів визначається з припущень, якеі принципово не відносяться до роботи алгоритму. Наприклад, відповідно до динамики зміни порогу розщеплення (злиття) кластерів. Такі алгоритми мають багато вад, але, завдяки побудованим дендрограмам, надають найбільш повне уявлення щодо структури кластерів.
Ієрархічні алгоритми діляться на дві великі групи.
1. Агломеративні, які послідовно об’єднують початкові елементи і відповідно зменшують кількість кластерів (побудова кластерів знизу до верху). На першому кроці вся початкова множина І подається як множина одноелементних кластерів. Далі рекурсивно два найближчих між собою кластери об’єднуються до одного спільного кластеру. На закінчення процедури отримуємо один кластер, що співпадає з початковою множиною І.
2. Дівізимні (такі, що діляться), в яких кількість кластерів збільшується, починаючі з одного, внаслідок чого утворюється послідовність розчіплюючих груп (побудова кластерів зверху до низу). На початку роботи алгоритму вся початкова множина І подається одним кластером, після чого на кожному кроці алгоритму один з існуючих кластерів рекурсивно ділиться на два дочірніх. Даний підхід використовують, коли всю початкову множину об’єктів необхідно розділити на відносно не велику кількість кластерів. За ядро нового кластеру С2 на першому етапі може обиратись, наприклад, елемент з найбільшою середньою відстанню від інших елементів початкового кластеру С1. На кожному наступному кроці елемент з кластеру С1 з найбільшою різницею між середньою відстанню до елементів, що знаходяться у С2, і середньою відстанню до елементів що залишаються у С1, переноситься до С2. Це продовжується доти, доки відповідні різниці не стануть від’ємними, тобто, доки існують елементи розташовані до елементів кластеру С2 ближче, ніж до елементів кластеру С1. рекурсивне розщеплення кластерів триває доки всі кластери не стануть сіглетонами (одноелементними), або доки усі члени одного кластера не будуть мати нульову відмінність один від іншого.
Найбільш популярними алгоритмами є все ж таки не ієрархічні методи, засновані на пошуку оптимального (у певному сенсі) розбиття множини даних на групи (кластери), шляхом мінімізації (максимізації) відповідної цільової функції .
Досліджувані дані подаються як множини векторів у багатовимірному просторі, координатами яких є атрибути (числові або категоріальні). Перед кластеризацією намагаються здійснити очистку і нормування даних. Очистка полягає у вилучені залежних атрибутів, які не вплинуть на результат но збільшать час, необхідний для обробки даних. Нормування забезпечує подання кожного атрибуту значенням з одиничного інтервалу для виключення впоиву на результати кластеризації різних областей значень окремих атрибутів.
Основним результатом неієрархічної кластерізації є матриця розбиття, яка подається таблицею, кожна комірка якої містить значення функції належності даного вектора заданому кластеру. Часто в результатом кластеризації є також таблиця центрів кластерів – векторів, ступень належності якого даному кластеру є максимальною.
Розглянемо приклад роботи класичного алгоритму кластерізації k-means. Нехай задано набір з 8 точок у двовимірному просторі, який треба розбити на два кластери:
| A | B | C | D | T | F | G | H |
| (1;3) | (3;3) | (4;3) | (5;3) | (1;2) | (4;2) | (1;1) | (2;1) |
Корок 1. Задамо (визначимо) кількість кластерів, на яку треба розбити початкову множину: k=2.
Крок 2. Випадковим чином визначимо дві точки m1=G і m2=Н, як центри кластерів.
Крок 3, прохід 1. Для кожної точки визначимо найближчий до неї центр кластеру у евклідовій метриці, тим самим визначаючі, до якого кластеру вона відноситься.
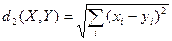 ,
,

| Точка | A | B | C | D | E | F | G | H |
| Відстань до m1 | 2,00 | 2,83 | 3,61 | 4,47 | 1,00 | 3,16 | 0,00 | 1,00 |
| Відстань до m2 | 2,24 | 2,24 | 2,83 | 3,61 | 1,41 | 2,24 | 1,00 | 0,00 |
| Кластер |
Визначивши належність точок кластерам, обчислюємо суму квадратів помилок:
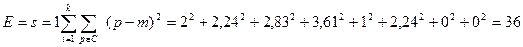 ;
;
Крок 4, прохід 1. Для кожного кластера обчислюється центроїд, до якого переміщається центр кластеру. Ц1= [(1+1+1/3);(3+2+1/3)]=(1;2); Ц2= [(3+4+5+4+2/5);(3+3+3+2+1/5)]=(3,6;2,4).

Крок 3, прохід 2. Для кожної точки знов визначається найближчий до неї центр нових кластерів і відповідна належність її до цього кластеру:
| Точка | A | B | C | D | E | F | G | H |
| Відстань до m1 | 1,00 | 2,24 | 3,16 | 4,12 | 0,00 | 3,00 | 1,00 | 1,41 |
| Відстань до m2 | 2,67 | 0,85 | 0,72 | 1,52 | 2,63 | 0,57 | 2,95 | 2,13 |
| Кластер |
Бачимо, що відносно велика зміна значення m2 призвела до того, що точка Н оказалась ближче до центру m1 і автоматично стала членом кластеру 1. Нова сума квадратів помилок склала:
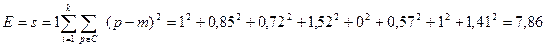
Помилка зменшилось, що означає більш «щільне» групування об’єктів відносно центрів кластерів.
Крок 4, прохід 2. Обчислюємо нові центроїди для кожного кластеру:
Ц1= [(1+1+1+2/4);(3+2+1+1/4)]=(1,25;1,75); Ц2= [(3+4+5+4/4);(3+3+3+2+/4)]=(4;2,75).
У порівнянні з минулим проходом центри кластерів мало змінилася.

Крок 3, прохід 3. Знов визначаємо відстань кожної точки від найближчого з центрів нових кластерів:
| Точка | A | B | C | D | E | F | G | H |
| Відстань до m1 | 1,27 | 2,15 | 3,92 | 3,95 | 0,35 | 2,76 | 0,79 | 1,06 |
| Відстань до m2 | 3,01 | 1,03 | 0,25 | 1,03 | 3,09 | 0,75 | 3,47 | 2,66 |
| Кластер |
Нова сума квадратів помилок склала:
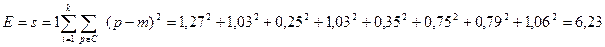
Сума квадратів помилок мала змінилась відносно попереднього проходу.
Крок 4, прохід 3. Знов обчислюються нові центроїди кластерівю Але, оскільки жодний об’єкт не змінив свого членства у кластерах і положення центроїдів практично не змінилося, алгоритм завершує свою роботу.
Одним з основних недоліків алгоритму k-means є відсутність критерію для вибору оптимальної кількості кластерів. Але, оскільки на початковому етапі дослідження даних, де й використовується кластерізація, апріорні відомості про особливості даних відсутні, аналітику приходиться діяти методом спроб і помилок. При цьому вибір меншого значення кількості кластерів призведе до того, що якісь групи об’єктів виявляться «розпиленими» по «чужим» кластерам і не будуть виявлені. Це може призвести до втрати цінних знань. З іншого боку, появлення в одному кластері об’єктів з «чужих» груп може значно ускладнити інтерпретацію результатів аналізу даних. Вибір же більшої за оптимальну кількості кластерів призведе к виділенню «зайвих» груп об’єктів і також може призвести до втрати знань про якусь загальну закономірність.
Для розв’язання даної проблеми у різних конкретних задачах побудована велика кількість алгоритмів, що дозволяють здійснювати автоматичний вибір кількості кластерів, оптимального з точки зору певного критерію. Зазвичай, в них будується кілька моделей для різних значень k, після чого вибирається найкраща за прийнятим критерієм.
Одним з найбільш популярних алгоритмів з автоматичним вибором кількості кластерів є алгоритм G-means. Він базується на припущенні про те, що дані, які кластерізуються, підпорядковуються деякому унімодальному закону розподілу, наприклад, гаусовському (звідки і назва алгоритму). Тоді центр кластера, визначений як середнє значення ознак потрапивши до нього об’ктів, може розглядатися як мода відповідного розподілу. Якщо ж початкові дані описуються унімодальним гаусовським розподілом із заданим серднім, можна припустити, що всі вони відносяться до одного класу. Якщо з розподіл не є гаусовським, то можна спробувати здійснити розбиття даних на два кластери. Якщо у цих двох кластерах розподіли будуть близькими до гаусовських, можна вважати, що у першому наближені k=2. Інакше, слід далі розбивати дані на більшу кількість кластерів, аж доки розподіл в кожному з них не стане достатньо близьким до гаусовського. Така модель і відповідна кількість кластерів будуть вважатись оптимальними.
Дата добавления: 2015-12-08; просмотров: 3749;
