Поняття кластерізації

Кластерізація є однією з задач Data Mining, яка полягає у розбитті досліджуваного множини об’єктів на групи відповідно до близькості їх властивостей. Кожен кластер складається зі схожих об’єктів, а об’єкти різних кластерів – суттєво відрізняються між собою. Процедура кластеризації ставить у відповідність будь-якому об’єкту х 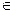Х мітку кластера y 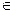Y.

На відміну від задачі класифікації, яка є віднесення кожного об’єкту даних до одного (або кількох) заздалегідь визначених класів і побудови моделі, яка визначає розподіл об’єктів між класами, в задачею кластеризації є віднесення об’єкту даних до одного (чи кількох) заздалегідь не визначених класів. Розподіл об’єктів по кластерам виконується при одночасному їх формуванні. Визначення кластерів і розбиття по ним об’єктів подається в підсумковій моделі даних, яка і є розв’язком задачі кластеризації.

Складність і неоднозначність задачі кластеризації полягає у тому, що:

- оптимальна кількість кластерів у загальному випадку невідома;

- вибір міри «схожості» властивостей об’єктів, як і критерію якості кластеризації, частіше за все носить суб’єктивний характер.

Задача кластеризації є дуже поширеною у багатьох практичних галузях де для її використання використовують інші терміни: таксонометрія, сегментація, групування, самоорганізація.

Цілі кластерізації можуть значно різнитися і залежать від конкретної задачі. До більш поширених задач відносять такі.

1. Вивчення даних – розбиття даних на групи допомагає виявити внутрішні закономірності. зробити дані більш наочними, висунути нові гіпотези. Зрозуміти, наскільки інформативними є властивості об’єктів. Наприклад, при кластерізації клієнтів, які брали кредити, дуже маленьким виявився кластер під назвою «Молодь», куди увійши працюючі студенти і молоді люди віком до 23 років. Виявилось, що банк не мав кредитних відділень у тих районах міста, де були зосереджені університети. Міграційна служба за рахунок кластеризації змогла виявити окремі змістовні групи серед тих, хто переїхав з сіл, о міст: «Бабусі» - жінки віком більше 60 років, діти яких мешкають у містах; «демобілізовани солдати», «невісти» і т.ін.

2. Полегшення аналізу – за рахунок кластерізації можна спростити подальшу обробку даних і побудови моделей для кожного окремого кластеру. Тобто. кластерізація може виступати попереднім, підготовчим, етапом перед розв’язком інших задач Data mining: класифікації, регресії, асоціації, послідовних шаблонів і т. ін. Наприклад, при попередній кластеризації покупців, значно простіше побудувати окремі асоціативні правила для кожного окремого їх сегменту.

3. Стиснення даних – за рахунок збереження лише найбільш типових об’ектів кожного кластеру.

4. Прогнозування – при віднесенні нового об’єкту до певного кластеру з’являється можливість прогнозування його поведінки, вважаючи, що вона буде схожою з поведінкою інших об’єктів кластеру. При кластеризації осіб. Що взяли авто кредити було виділено кластер молодих чоловіків віком 23 – 28 років, які жили у московській області менше року і мали значні затримки з виплатою кредитів, оскільки або переоцінювали свої сили, або були шахраями. Ця інформація була врахована при побудові скорингових карт.

5. Виявлення аномалій (outlier detection) –за рахунок виявлення кластерів, до яких потрапляє дуже мала кількість «не типових» об’єктів. Завдяки кластеризації осіб, застрахованих від нещасних випадків було виявлено невеличкий кластер, е часто повторювались прізвища одних й тих самих лікарів і не значно змінювались суми страхових виплат. Здійснена перевірка виявила, що у 90% таких випадків мав місце зговір з лікарями.

Треба розуміти, що сама по себе кластерізація не надає якихось результатів аналізу. Для отримання ефекту необхідно виконати змістовну інтерпретацію кожного кластера, що передбачає присвоєння кожному кластеру інформаційно наповненої назви. Що відображає його сутність, наприклад, «розлучені молоді мами», «дачники», «працюючи студенти» і т. ін. Інтерпретація потребує ретельного дослідження кожного кластеру: його статистичних характеристик, розподілу значень об’єктів у кластері, оцінювання потужності кластеру і т. ін.. Значно полегшує інтерпретацію візуалізація даних, подання результатів у вигляді спеціальних дендограм, кластерограм, карт і т. ін.

У Data Mining найбільш розповсюдженою мірою оцінки близькості між об’єктами є метрика, яка є правиломабо обчислення відстані між об’єктами, поданими у вигляді точок у m-вимірному просторі R^m. Найбільш популярними метриками є такі.

1. Евклідова відстань, або метрика L₂, обчислює відстань за такою формулою:

,

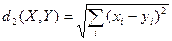де Х ={х₁, х₂, …, х_j,…х_n}, Y={y₁, y₂, …, y_j,…y_n} – вектори ознак двох записів.

Оскільки множина точок рівновіддалених від центра при цій метриці утворює сферу, кластери, отримані з її використанням також мають близьку до сферичної форму. Також ця метрика надає більші значенням вагам більш віддаленим один від одного об’єктам.

2. Манхетенська відстань, або метрика L₁, обчислюється за формулою:

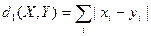
Ця «відстань міських кварталів» визначає найкоротшу відстань між двома точками, пройдену по лініям, паралельним осям прямокутної системи координат. Використання прямокутної системи координат часто дозволяє зменшити вплив аномальних значень на роботу алгоритмів і будує кластери, форма яких прагне до кубічної.

3. Хемінгова відстань – є середнім різниць по координатам:

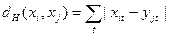
Схожа з евклідовою відстанню, але зменшує вплив окремих великих різниць (оскільки відстані не підносяться до степеню).

4. Відстань Чебишева – використовуються коли важливо розрізнити два об’єкти, які розрізняються однією координатою (одним виміром):

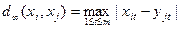
5. Відстань Махаланобіса - визначається як відстань від точки спостереження до центру ваги в багатовимірному просторі, визначеному корельованими (неортогональними) незалежними змінними. Цей захід дозволяє, зокрема, визначити чи є дане спостереження викидом по відношенню до решти значень незалежних змінних. Якщо незалежні змінні не є корелірованими, то відстань Махаланобіса співпадає з евклідовим відстанню:

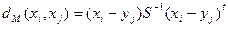
Де – S – коваріаційна матриця.

6. Пікова відстань – передбачає незалежність між випадковими змінними, що свідчить про ортогональний простір. Але у практичних застосуваннях ці змінні не є незалежними:

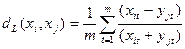
Конкретна метрика має вибиратися тільки з урахуванням інформації про характер даних.

Результатом кластерного аналізу є набір кластерів, що містять елементи початкової множини. Кластерна модель має описувати як самі кластери, так і належність кожного об’єкту до кожного з них.

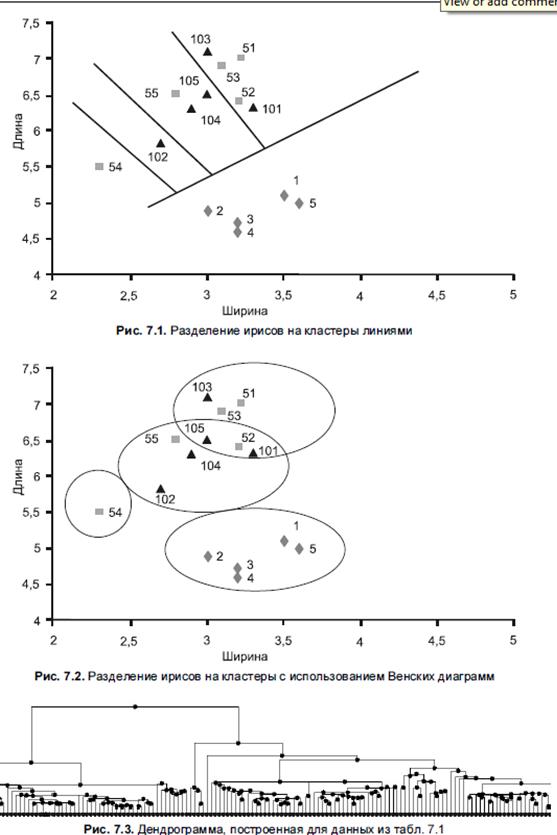
Для невеликих кількостей об’єктів, що характеризуються двома змінними, результати відображають графічно, розділяючи точки, що подають об’єкти прямими, які описуються лінійними функціями, або ломаними лініями, що описуються нелінійними функціями.

Якщо алгоритм не відносить елемент до кластеру з певною імовірністю, більш зручним буде подання у вигляді таблиці, де рядкі відповідають єлементам початкової множини, стовпці – отриманим кластерам, а в комірках наводяться значення імовірністей належності елемента кластеру.

Іерархічні алгоритми будують ієрархічні структури кластерів. На верхньому рівні початкова множина подається одним кластером, який ділиться на кілка кластерів на наступному рівні і т. д. такі ієрархії відображаються за допомогою спеціальних дендрограм, які відображають деревовидну структуру діаграм.