Похиле падіння променів на решітку

У 1927 р. американський учений А.Комптон і французький Ж.Тибо встановили, що у випадку, якщо|у разі , якщо,в случае | паралельний пучок падає на решітку під кутом|ріг,куток|, то для обчислення|підрахунок| положення|становище| головних максимумів можна поступати|надходити| так само, як у випадку нормального падіння променів.

Повна|цілковитий| різниця ходу для двох відповідних променів є:

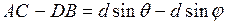. (см. рис.2.39)

Умови утворення головних максимумів:

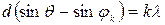, 2.32

де 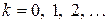Після перетворення, отримуємо:

.

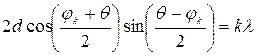Якщо решітка досить груба 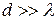, то кути|ріг,куток| дифракції малі, тобто кут|ріг,куток| 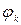мало відрізняється від 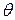, можна покласти:

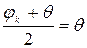і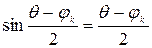

тобто 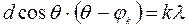, 2.33

а було 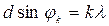або (див. формулу 2.28)

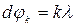(якщо 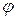мало). 2.34

Це порівняння показує, що кут|ріг,куток| між нульовим максимумом і вторинними|повторний| максимумами 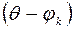обчислюється|обчисляється,вичисляти| так само, начебто|начебто| падіння було нормальним, але|та| решітка мала б зменшений період, а саме .

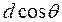Якщо кут 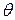близький|поблизу| до 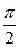, то ми маємо мало|дуже| помітне зменшення періоду. Таким чином, при падінні на грубі решітки променів під кутом|ріг,куток|, близьким до 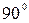, спостерігається виразна|чіткий| дифракційна картина. Наприклад, міліметрова лінійка при дуже косому падінні на неї променів дозволяє спостерігати дифракційні спектри для видимого світла.

Вказана обставина знайшла важливе|поважний| застосування|вживання| при дослідженні дифракції рентгенівських променів. Оскільки|тому що| довжини хвиль рентгенівських променів|звично| у тисячі разів менше, ніж хвилі видимого світла, то всі штучно побудовані|споруджені| решітки виявляються|опинятися| для рентгенівських променів досить|дуже| грубими:

.

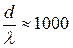Використовуючи дуже косе падіння, вдалося отримати|одержати| чітко виражену|виказану,висловлену| дифракцію рентгенівських променів із|із| порівняно грубими решітками ( 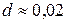мм, А.Комптон і У.Дуан, 1925 р.). Згодом цим методом були отримані|одержані| чудові дифракційні спектри і з|із| великою точністю виміряні довжини хвиль рентгенівських променів. Цей метод вимірювання|вимір| є|з'являтися,являтися| на сьогодні найбільш використовуваним.