Дифракційна решітка
Система великого числа паралельних щілин рівної ширини, розділених однаковими непрозорими проміжками, називається дифракційною решіткою.
Суму ширини прозорої і непрозорої ліній на решітці прийнято називати постійною або періодом решітки.
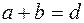 – період решітки.
– період решітки.
Дифракція на двох щілинах показує, що дифракційна картина в цьому випадку відрізняється від однієї щілини тим, що дифракційні максимуми стають вужчими і що між двома головними максимумами з'являється|появлятися| додатковий мінімум. Якщо взяти три щілини, то виявляється|опинятися|, що з'являється|появлятися| два додаткові мінімуми між двома головними максимумами при 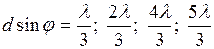 і т.д.
і т.д.
 Це легко показати на векторній діаграмі. Якщо
Це легко показати на векторній діаграмі. Якщо 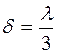 , то сума амплітуд, складаючись, дасть нуль; при
, то сума амплітуд, складаючись, дасть нуль; при 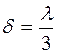 , зсув|зсув| фаз між сусідніми коливаннями дорівнює|рівнятися|
, зсув|зсув| фаз між сусідніми коливаннями дорівнює|рівнятися| 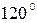 .
.

Якщо 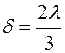 , то
, то 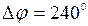 .
.
Якщо ми маємо 4 щілини, то між головними максимумами розташуються вже 3 додаткових мінімуми, при: δ= 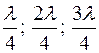 , відповідно
, відповідно 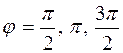 .
.



| Рис.2.33 |
Якщо ж ми матимемо 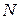 щілин, то загальну|спільний| умову можна записати так:
щілин, то загальну|спільний| умову можна записати так:
головні максимуми 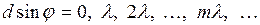 2.29
2.29
додаткові мінімуми 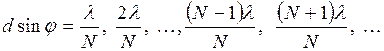 2.30
2.30
Тобто, між двома головними максимумами розташовується 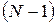 додаткових мінімумів, розділених вторинними|повторний| максимумами.
додаткових мінімумів, розділених вторинними|повторний| максимумами.

Рис.2.34
Звичайно, зі збільшенням кількості щілин росте|зростати| інтенсивність головних максимумів, оскільки|тому що| зростає кількість світла, що пропускається решіткою. Найістотніше|суттєвіше| ж те, що велика кількість щілин перетворює розпливчасті максимуми на різкі, вузькі максимуми, розділені практично темними проміжками, бо вторинні|повторний| максимуми дуже слабкі порівняно з основними. Найсильніший з|із| них складає не більше 5% від головного. Застосування|вживання| великої кількості щілин, призводить|призводити,наводити| до різкого розділення|поділ| ліній, що належать різним порядкам.
Освітлюючи дифракційну решітку монохроматичним світлом і розглядаючи|розглядуючи| зображення, отримані|одержані| у фокальній площині|плоскість| лінзи, поставленій перед решіткою отримаємо|одержимо| ряд|лава,низка| світлих ліній кольору|цвіт| світла, що пропускається.

Рис.2.35
Якщо пропустимо біле світло, то отримаємо|одержимо| ряд|лава,низка| спектрів, що починаються з фіолетового кольору|цвіт|.

Рис.2.36
Отримаємо|одержимо| ряд|лава,низка| спектрів різних порядків|лад|.
В якісних решітках 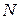 має порядок|лад| до
має порядок|лад| до 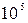 штук, тому спектр складається з дуже різких ліній.
штук, тому спектр складається з дуже різких ліній.
Відстань між головними максимумами для певної довжини хвилі 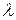 визначається періодом решітки
визначається періодом решітки 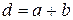 , а розподіл інтенсивності між окремими максимумами залежить від співвідношення між
, а розподіл інтенсивності між окремими максимумами залежить від співвідношення між 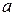 і
і 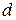 . У тому випадку, коли
. У тому випадку, коли 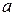 і
і 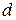 близькі за значенням, деякі головні максимуми будуть відсутні. Так, при
близькі за значенням, деякі головні максимуми будуть відсутні. Так, при 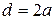 пропадають всі парні максимуми, причому відповідно, звичайно, посилюються|підсилюватися| непарні. При
пропадають всі парні максимуми, причому відповідно, звичайно, посилюються|підсилюватися| непарні. При 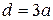 зникає кожен третій максимум і т.д. Інтенсивності максимумів зменшуються при переході до дальших порядків|лад|.
зникає кожен третій максимум і т.д. Інтенсивності максимумів зменшуються при переході до дальших порядків|лад|.
Отже, якщо ми маємо дифракційну решітку, то з|із| умови максимумів 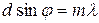 , цілком можна визначити
, цілком можна визначити 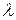 певного кольору|цвіт|, причому для
певного кольору|цвіт|, причому для 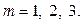
З|із| цієї ж умови видно|показно|, що спектри порядку|лад| більшого, ніж 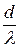 , видні|показний| не будуть, тобто не мають місця.
, видні|показний| не будуть, тобто не мають місця.
Оскільки|тому що| максимальне значення 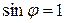 , то
, то
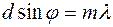 ;
;
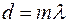 ;
;
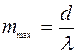 . .
|
2.31
Детальніших відомостей про розподіл енергії в дифракційній картині ця формула не дає, залишає без розгляду питання про роль числа штрихів на решітці.
Причому з|із| формули видно|показно|, що решіткою можна вимірювати|виміряти| лише ті довжини хвиль, для яких 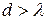 , оскільки|тому що| тільки|лише| в цьому випадку
, оскільки|тому що| тільки|лише| в цьому випадку 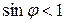 (адже
(адже 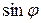 не може бути >1), якщо ж
не може бути >1), якщо ж 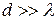 , то такими решітками також не можна користуватися, оскільки|тому що| максимуми будуть нескінченно віддаленими|віддалений|.
, то такими решітками також не можна користуватися, оскільки|тому що| максимуми будуть нескінченно віддаленими|віддалений|.

Рис.2.37
У центрі нульовий max, симетрично по обидві сторони розташовуються спектри вищих порядків|лад|. Відстань між відповідними лініями спектрів зростає у міру збільшення порядку|лад| спектру.
Залежно від спектральної однорідності аналізованого світла, тобто відмінності крайніх довжин хвиль, його складових, спектри вищих порядків|лад| починають|розпочинати,зачинати| накладатися один на одного. Наприклад, для сонячного світла спектри другого і третього порядків|лад| уже частково перекривають один одного.
Наприклад:

Рис.2.38
Дата добавления: 2016-02-09; просмотров: 1345;
