Багатопроменева інтерференція
| |
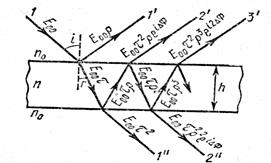 Рис.2.16 Рис.2.16
|
Проте|однак| у випадках, коли інтенсивності багато разів відбитих променів близькі один до одного, врахування|урахування| їх внеску|вклад| в загальну|спільний| інтенсивність є|з'являтися,являтися| обов'язковим.
Реалізація згаданого випадку — випадку багатопроменевої інтерференції — визначається значеннями коефіцієнтів відбивання і пропускання.
Обчислення|підрахунок| інтенсивностей променів, що пройшли через пластинку|платівка| і відбитих від неї. Формули Ейрі.Нехай|нехай| плоска монохроматична світлова хвиля падає під кутом|ріг,куток| і на поверхню плоскопараллельної прозорої пластинки|платівка| (рис.2.16). Показники заломлення пластинки|платівка| і навколишнього середовища відповідно будуть п і 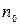 Коефіцієнти відбивання і пропускання за інтенсивністю позначимо відповідно через R і Т. Якщопоглинанням усередині пластинки|платівка| можна нехтувати, то
Коефіцієнти відбивання і пропускання за інтенсивністю позначимо відповідно через R і Т. Якщопоглинанням усередині пластинки|платівка| можна нехтувати, то
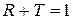
| 2.12 |
Зважаючи на|внаслідок,унаслідок| те, що втрата півхвилі при відбиванні призводить|призводити,наводити| всього лише до зсуву|зміщення| всієї інтерференційної картини на пів лінії, її в наших розрахунках можна не брати до уваги. Унаслідок|внаслідок| багаторазового|багаторазовий| відбивання на межі|кордон| розподілу виникне сукупність відбитих паралельних променів та тих, які пройшли крізь пластинку|платівка|. Цікаво розглянути|розгледіти| багатопроменеву інтерференцію як відбитих|відбитих|, так і таких, що пройшли|минули,спливли| промені, тобто знайти розподіл відповідних інтенсивностей. Для цього треба скласти амплітуди взаємно паралельних променів з урахуванням|з врахуванням| різниці ходу (фаз) між ними. Очевидно, що різниця ходу між двома сусідніми променями, що вийшли (відбитими або ж такими, що пройшли|минули,спливли|) з пластинки|платівка|, рівна
 , 2.13
, 2.13
де h — товщина пластинки|платівка|, r — кут|ріг,куток| заломлення. Цій різниці ходу відповідає різниця фаз:
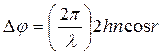 ,2.14
,2.14
де 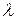 — довжина падаючої хвилі у вакуумі.
— довжина падаючої хвилі у вакуумі.
Позначимо амплітудні коефіцієнти відбивання (відношення|ставлення| амплітуд відбитої і падаючої хвиль) і пропускання (відношення|ставлення| амплітуд хвилі, яка пройшла, і падаючої хвилі) через  і
і 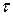 . Нехай|нехай| амплітуда падаючої лінійно-поляризованої світлової хвилі буде
. Нехай|нехай| амплітуда падаючої лінійно-поляризованої світлової хвилі буде 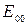 (рис.2.16). При кожному проходженні через межу|кордон| розподілу пластинка|платівка| — повітря амплітуда хвилі зменшується в
(рис.2.16). При кожному проходженні через межу|кордон| розподілу пластинка|платівка| — повітря амплітуда хвилі зменшується в 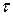 раз, а при кожному відбиванні від такої межі|кордон| вона зменшується в
раз, а при кожному відбиванні від такої межі|кордон| вона зменшується в  раз. Внаслідок цього амплітуди хвиль, що пройшли крізь пластинку,|платівка| і відбитих|відбитих| від неї променів відповідно рівні
раз. Внаслідок цього амплітуди хвиль, що пройшли крізь пластинку,|платівка| і відбитих|відбитих| від неї променів відповідно рівні 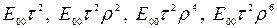 і
і 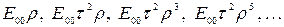 і т.д. У виразі|вираження| для амплітуди різницю фаз між сусідніми променями можна врахувати введенням|вступ| відповідного множника. Враховуючи це, сумарні амплітуди для хвиль, що пройшли, і відбитих у разі|в разі| достатньо довгої пластинки|платівка| будуть
і т.д. У виразі|вираження| для амплітуди різницю фаз між сусідніми променями можна врахувати введенням|вступ| відповідного множника. Враховуючи це, сумарні амплітуди для хвиль, що пройшли, і відбитих у разі|в разі| достатньо довгої пластинки|платівка| будуть
 , 2.15
, 2.15
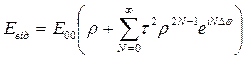 2.16
2.16
де N — число променів, що інтерферують.
Підсумовування, виконане для випадку, коли падіння інтенсивності пучків, що складаються, йде достатньо|досить| швидко, призводить|призводити,наводити| до такого результату:
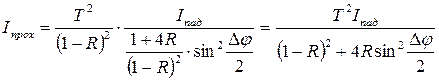 2.17
2.17
 2.18
2.18
де  ,
, 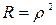 .
.
Вирази (2.17) і (2.18) називаються формулами Ейрі.
 Залежність інтенсивності відбитих пучків та тих, що проходять|минати,спливати|, від різниці фаз
Залежність інтенсивності відбитих пучків та тих, що проходять|минати,спливати|, від різниці фаз
Якщо плоскі світлові хвилі однакової інтенсивності направити|спрямувати,скерувати| на пластинку|платівка| під кутами|ріг,куток|, що мало розрізняються, то у фокальній площині|плоскість| лінзи (рис. 2.17), поставленої перед відбитими (або ж тими, що пройшли|минули,спливли|) пучками, з'являються|появлятися| інтерференційні лінії рівного нахилу. Положення|становище| максимумів і мінімумів
| Рис.2.17 |

| Рис.2.18 |
Рис. 2.18
визначатимуться значеннями різниці фаз. Оскільки|тому що|  змінюється від нуля (при
змінюється від нуля (при  ) до одиниці [при
) до одиниці [при  ], то, згідно (2.15) і (2.16), інтенсивності змінюється безперервно, досягаючи мінімуму і максимуму при даних R і Т. Максимальнеі мінімальні значення інтенсивностей залежно від R і Т виражаються|виказуються,висловлюються| наступними|слідуючий| формулами:
], то, згідно (2.15) і (2.16), інтенсивності змінюється безперервно, досягаючи мінімуму і максимуму при даних R і Т. Максимальнеі мінімальні значення інтенсивностей залежно від R і Т виражаються|виказуються,висловлюються| наступними|слідуючий| формулами:
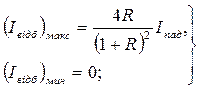 2.19
2.19
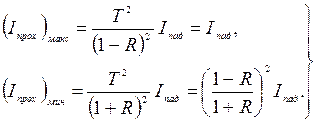 21.20
21.20
Отже, в світлі, яке пройшло, максимуми спостерігаються при  , а мінімуми – при
, а мінімуми – при 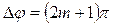 , тобто порядок|лад| інтерференції т, визначуваний як
, тобто порядок|лад| інтерференції т, визначуваний як  , рівний цілим числам 0, 1, 2, 3 ... для максимумів і напівцілим числам 1/2, 3/2, 5/2 для мінімумів. У відбитому світлі максимуми інтенсивностей відповідають напівцілим значенням порядку|лад| інтерференції т = 1/2, 3/2, 5/2, мінімуми – цілим числам т = 0, 1, 2 ... і т.д. Таким чином, положення|становище| ліній у відбитому світлі, та у тому, що пройшло|минуло,спливло|, аналогічне відповідним картинам інтерференції при врахуванні|урахування| тільки|лише| двох перших
, рівний цілим числам 0, 1, 2, 3 ... для максимумів і напівцілим числам 1/2, 3/2, 5/2 для мінімумів. У відбитому світлі максимуми інтенсивностей відповідають напівцілим значенням порядку|лад| інтерференції т = 1/2, 3/2, 5/2, мінімуми – цілим числам т = 0, 1, 2 ... і т.д. Таким чином, положення|становище| ліній у відбитому світлі, та у тому, що пройшло|минуло,спливло|, аналогічне відповідним картинам інтерференції при врахуванні|урахування| тільки|лише| двох перших
|
Графіки залежності інтенсивностей від різниці фаз 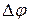 при даному значенні R представлені|уявлені| на рис. 2.18. Як випливає з графіків, сума
при даному значенні R представлені|уявлені| на рис. 2.18. Як випливає з графіків, сума 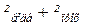 залишається постійною і рівною інтенсивності падаючого пучка. Інтенсивність світла, що проходить|минати,спливати|, відрізняється від нуля при всіх значеннях
залишається постійною і рівною інтенсивності падаючого пучка. Інтенсивність світла, що проходить|минати,спливати|, відрізняється від нуля при всіх значеннях 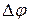 (рис. 2.18), тоді як інтенсивність відбитого світла при
(рис. 2.18), тоді як інтенсивність відбитого світла при  і т.д. стає рівною нулю.
і т.д. стає рівною нулю.
Залежності інтенсивності відбитих та тих пучків, що пройшли|минули,спливли|, від коефіцієнта відбивання|відображення,відбиття|.Оскільки|тому що| інтенсивності відбитих пучків та тих, що пройшли|минули,спливли|, залежать від коефіцієнта відбивання (в даному випадку  ), то цікаво проаналізувати ці залежності. Досить виконати|проробити| це для одного випадку, наприклад для світла, яке пройшло.
), то цікаво проаналізувати ці залежності. Досить виконати|проробити| це для одного випадку, наприклад для світла, яке пройшло.
Як випливає з рис. 2.19, зі збільшенням R (при наближенні його до одиниці) інтенсивність мінімумів інтерференційної картини в світлі, яке пройшло, зменшується, максимуми ж стають різкішими. Отже, інтерференційна картина при  є сукупністю вузьких світлих ліній на практично темному фоні.
є сукупністю вузьких світлих ліній на практично темному фоні.
Різкість ліній.Інтерференційну картину можна характеризувати величиною так званої різкості ліній. Цей параметр прийнято вимірювати|виміряти| напівшириною лінії. В даному випадку вона дорівнює відстані між точками|точка|, що відповідають половині максимального значення інтенсивності. Як параметр різкості F інтерференційної картини можна взяти відношення|ставлення| відстані між сусідніми лініями до напівширини 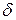 . Згідно з визначенням напівширини лінії
. Згідно з визначенням напівширини лінії
 . 2.21
. 2.21
Це має місце при  . Оскільки|тому що|
. Оскільки|тому що| 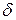 – мала величина, то можна прийняти
– мала величина, то можна прийняти 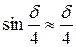 . Підставляючи значення
. Підставляючи значення 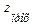 у формулу (2.21), маємо
у формулу (2.21), маємо

Звідси
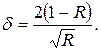
Оскільки|тому що| відстань між сусідніми лініями відповідає зміні 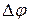 на
на 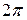 , то для різкості ліній F маємо
, то для різкості ліній F маємо
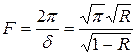 . 2.22
. 2.22
При 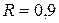 F має значення, трохи|ледве| менше 30, тобто відстань між двома сусідніми максимумами приблизно в 30 разів більше ширини кожного з них.
F має значення, трохи|ледве| менше 30, тобто відстань між двома сусідніми максимумами приблизно в 30 разів більше ширини кожного з них.

Рис.2.19
При спостереженні багатопроменевої інтерференції в білому світлі лінії забарвлюються в різні кольори|цвіт|. Лінії, що належать різним довжинам хвиль, у світлі, що проходить|минати,спливати|, розділяються чіткіше. Велике практичне значення багатопроменевої інтерференції обумовлене саме цим фактом.
Як відомо, в оптичному діапазоні коефіцієнт відбивання при нормальному падінні променя для межі|кордон| повітря — скло рівний приблизно 0,04. Збільшення R при похилому падінні променя не є|з'являтися,являтися| достатнім для отримання|здобуття| різкої багатопроменевої інтерференційної картини в світлі, що проходить|минати,спливати|. Коефіцієнт відбивання|відображення,відбиття|, близький до одиниці, можна отримати|одержати| і при майже нормальному падінні світла — шляхом нанесення відповідних багатошарових діелектричних покриттів або частково прозорого шару металу.
Дата добавления: 2016-02-09; просмотров: 1065;
