Замкнутая проводящая оболочка
В состоянии равновесия избыточных зарядов внутри сплошного проводника нет. Такое состояние сохраняется, если удалить внутреннюю часть проводника, т. е. образуется замкнутая полость. Если внутри полости нет зарядов, то электрическое поле в ней отсутствует. Заряд проводника всегда располагается на его внешней поверхности и не создает в полости электрического поля. Это явление было тщательно изучено Фарадеем и получило название - электростатического экранирования. Для защиты, от влияния внешних постоянных и переменных электрических полей, измерительных приборов, блоков теле-, радиоаппаратуры и т. д., их окружают густой проводящей сеткой. Поместим внутри замкнутой полости произвольное число
 Рис. 3
Рис. 3
|
зарядов. Пусть внешнее пространство, окружающее проводник с полостью заполнено проводящей средой. Электрическое поле в ней при равновесии равно нулю, т. е. среда электрически нейтральна и не содержит избыточных зарядов.
Поскольку всюду внутри проводника электрическое поле отсутствует (Е = 0), то поток вектора Фэ сквозь произвольную замкнутую поверхность, окружающую полость, также равен нулю.
Следовательно, согласно теореме Гаусса, алгебраическая сумма зарядов внутри полости равна нулю.
Поэтому алгебраическая сумма индуцированных зарядов на внешней поверхности полости равна по модулю алгебраической сумме зарядов внутри этой полости. В состоянии равновесия, индуцированные заряды на внутренней поверхности полости располагаются таким образом, чтобы полностью компенсировать вне полости электрическое поле, созданное зарядами находящимися внутри полости (рис. 3).
В связи с тем, что проводящая среда, окружающая полость, всюду электрически нейтральна, то она никак не влияет на электрическое поле.
Следовательно, ее можно удалить, сохранив только проводящую оболочку вокруг полости.
Вывод: электрическое поле зарядов внутри замкнутой проводящей оболочки и зарядов, индуцированных на внутренней поверхности полости, равно нулю в каждой точке окружающего внешнего пространства.
Любое перемещение зарядов внутри оболочки не вызывает изменений электрического поля во внешнем пространстве, т. е. распределение зарядов на наружной поверхности оболочки не нарушится.
Это относится и к электрическому полю внутри полости (при наличии зарядов) и к распределению зарядов на внутренней поверхности полости, если менять конфигурацию зарядов вне оболочки.
Это положение справедливо только для электростатических полей.
Совокупность явлений, связанных с индуцированием зарядов в веществах, при внесении их во внешнее электрическое поле, называют теоремой Фарадея. Рассмотренные явления позволяют зарядить проводники электризацией через влияние, т. е. не касаясь поверхности проводника заряженным телом.
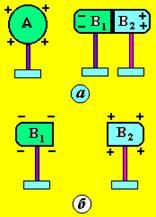 Рис. 4
Рис. 4
|
Например, незаряженный проводник, состоящий из двух частей В1 и В2, приблизить к положительно заряженному проводнику А, то слева индуцируется отрицательный избыточный заряд, а справа - положительный (рис. 4, а). Не удаляя тело А, разъединим В1 и В2.
На теле В1 останется избыточный отрицательный заряд, а на В2 - избыточный положительный заряд (рис. 4, б).
Если заряженное тело А привести в соприкосновение с таким же по размерам не заряженным телом Б, то половина заряда с тела А перейдет на тело Б пока их потенциалы не станут равными, что имеет решающее значение для объяснения существования тока в проводниках.
В результате тела будут отталкиваться друг от друга (рис. 5, а, б).
Однако, если тело Б представляет собой, например, пустотелый шар, а заряд с тела А переносится с помощью пробника с изолирующей ручкой на тело Б (рис. 6), но касаясь его внутренней поверхности, то в этом случае весь заряд с пробника полностью перейдет
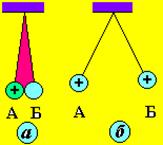 Рис. 5
Рис. 5
|
на внешнюю поверхность тела Б. Для измерения потенциала и заряда (поверхностной плотности заряда) используют электрометр (рис. 6). Он состоит из цилиндрического металлического корпуса, основания которого закрыты стеклом. Корпус заземляют во время проведения опыта. Внутрь введен металлический стержень, изолированный от корпуса. На нижнем его конце укреплена легкая, подвижная
металлическая стрелка. На верхний конец стержня можно надевать съемные металлические проводники различной формы и размеров.
 Рис. 7
Рис. 7
|
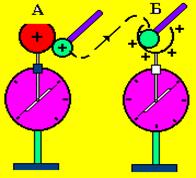 Рис. 6
Рис. 6
|
При сообщении стержню заряда стрелка отклоняется от стержня тем сильнее, чем больше возникающая разность потенциалов между стрелкой и заземленным корпусом электрометра. Перед измерением электрометр градуируют. Такие электрометры позволяют измерять разность потенциалов до 1,5 ×104 В. Для измерений разности потенциалов до 105 В, используют струнные и абсолютные электрометры. Передача проводнику полного заряда с пробника нашла применение в генераторе Ван-де-Граафа (рис. 7), позволяющем получать электрические поля напряженностью до 107 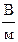 . В этом случае используют два генератора: один заряжают положительно, другой - отрицательно.
. В этом случае используют два генератора: один заряжают положительно, другой - отрицательно.
Электрические поля применяется для ускорения электронов и ионов.
В электростатическом генераторе для переноса электрических зарядов используется диэлектрический транспортер в виде гибкой бесконечной ленты. С помощью пластин или щеток заряд с ленты переносится на внутреннюю поверхность сферического проводника диаметром 2 м. Дальнейшее увеличение электрического поля генератора невозможно из-за пробоя воздуха.
Явления, связанные с электризацией, часто встречаются в природе. Например, огни святого Эльма; свечение Анд - красно-сине-фиолетовое свечение с характерным треском; коронный разряд, наблюдается во время грозы на морских судах при стекании зарядов с высоких остроконечных предметов при пробое воздуха (мачт, антенн, крыльев самолетов и т. д.).
Стекание зарядов с остроконечных предметов можно наблюдать на ряде опытов: вращение легкого цилиндра, колесо Франклина - стекание зарядов с остриев (электрический ветер) приводит во вращение легкий крест из металлических проволочек.
Вращение креста происходит потому, что воздух вблизи ее острия - ионизирован. В сильном электрическом поле, образовавшиеся ионы и острия оказываются заряженными одинаково и отталкиваются.
Для защиты зданий от гроз используют молниеотводы - высокие металлические заземленные мачты. Мощные грозовые явления в атмосфере Земли заряжают ее отрицательным зарядом. Атмосферное электричество изучали Ломоносов, Франклин, Рихман (погиб во время эксперимента) и др. Иногда грозы сопровождаются образованием шаровых молний.
4. Уравнения Пуассона и Лапласа
Общая задача электростатики заключается в том, что если неизвестно распределение зарядов, но известны потенциалы проводников, их относительное расположение и форма, то можно определить потенциал в любой точке электростатического поля между проводниками. Зная потенциал j, можно найти напряженность поля 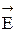 , что даст возможность указать распределение поверхностных зарядов проводников.
, что даст возможность указать распределение поверхностных зарядов проводников.
Для нахождения дифференциального уравнения, которому удовлетворяет функция j - потенциал, воспользуемся дифференциальной формой теоремы гаусса.
Решив совместно эти уравнения, получим общее дифференциальное уравнение Пуассона - уравнение для потенциала в виде
 , (2)
, (2)
где Ñ2 - оператор Лапласа, который в декартовых координатах записывается в виде 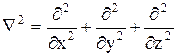 .
.
При отсутствии зарядов между проводниками уравнение Пуассона переходит в уравнение Лапласа, т. е.
Ñ2j = 0. (3)
Уравнения Пуассона и Лапласа позволяют решить общую задачу электростатики, решение которой является единственным (теорема единственности).
Дата добавления: 2016-02-09; просмотров: 3754;
