Стоячие электромагнитные волны. Пусть распространяются две плоские одинаковые монохроматические электромагнитные волны навстречу друг другу вдоль оси У.
Пусть распространяются две плоские одинаковые монохроматические электромагнитные волны навстречу друг другу вдоль оси У.
Векторы напряженности этих волн лежат в одной плоскости и совершают колебания по гармоническому закону:
E1 = E0 sin (wt – kу), (28)
E2 = E0 sin (wt + kу). (29)
После сложения результирующий вектор напряженности электрического поля по модулю электромагнитной волны принимает вид:
Eрез = 2E0× сos kу×sin wt, (30)
Результирующий вектор индукции магнитного поля по модулю электромагнитной волны принимает вид:
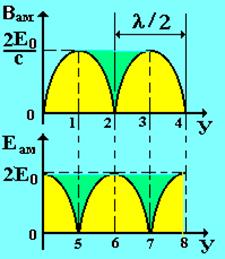
| Рис. 9 |
|
Врез = –2E0/c× sin kу×cos wt. (31)
Из анализа полученных уравнений следует: 1. процесс распространения волн локализован в некоторой области и называется стоячей электромагнитной волной; 2. Волна не является бегущей;
3. В стоячей волне оба поля сдвинуты по фазе на p/2.
Из этого следует, что в стоячей волне происходит превращение электрической энергии в магнитную энергию, а затем, магнитной энергии в электрическую энергию. В бегущей же волне, из-за сифазности, не происходит превращение электрической энергии в магнитной энергию. На рис. 9 точки 1 и 3 являются магнитными пучностями; точки 0, 2, 4 – являются магнитными узлами; точки 0, 6, 8 – являются электрическими пучностями; точки 5, 7 – являются электрическими узлами. Распространенным способом получения стоячих электромагнитных волн является зеркальное отражение перпендикулярно падающей волны. В своих опытах о взаимодействии света с веществом Винер использовал стоячие электромагнитные волны и доказал, что основную роль играет вектор 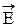 , а не вектор
, а не вектор 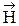 .
.
Дата добавления: 2016-02-09; просмотров: 1575;
