Начало и направление отсчета расстояния

На теле отсчета устанавливают начало и направление измерения расстояния.

Физические тела, в том числе и тело человека,в некоторых случаяхможно рассматривать как материальные точки.

Это возможно, если расстояние, на которое они передвигаются, несравнимо больше их собственных размеров и если можно пренебречь вращательным движением тела (например, при полете диска по траектории). Для точного определения спортив­ного результата правила соревнований строго предусматривают, по какой точке (пункт отсчета) ведется отсчет (по уровню лыжных креплений, по выступающей точке грудной клетки спринтера, по заднему краю следа приземляющегося прыгуна . и т. п.).

Итак, либо все движущееся тело рассматривают как материальную точку, до которой измеряют расстояние, либо на нем выделяют пункты отсчета. Расстояние измеряется от начала отсчета до пункта отсчета. В качестве такого пункта выбирается определенная точка движущегося тела человека. В случае вращательного движения выбирают линию отсчета.

Существует три основных способа определения движения точки: естественный, координатный и векторный.

При естественном способе заранее известна траектория точки; на ней следует выбрать начало (о) отсчета (например, контрольный пункт на трассе дистанции). Тогда положение точки (например, гон­щика) на траектории определяется расстоянием ее от начала отсчета (естественная координата). Надо еще указать, с какой стороны от на­чала отсчета (знаком + или —) расположена на траектории точка (рис. 17, а). Положение точки на линии определяется всего одним чис­лом со знаком + или —.

Координатный способ позволяет определить положение точки в ко­ординатах на плоскости и в пространстве. Чаще применяют прямоугольные координаты.

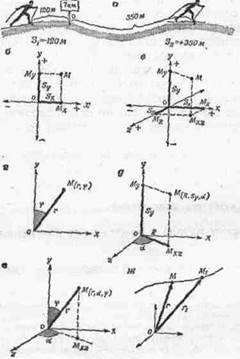
Рис. 17, Способы отсчета движения точки:

а — естественный способ; бвгде — координатный способ: и — на плоскости, в — в пространстве, г — полярные, д — цилиндрические, е — сфериче­ские; ж — векторный способ (ориг.)

Расстояние от начала коор­динат до проекции точки на все три оси (Мх, Му, А1,)— это три линейные коор­динаты: абсцисса, ордината и аппликата , полностью определяющие по­ложение точки в простран­стве. Можно пользоваться также и угловыми ко­ординатами: на плоско­сти — в системе полярных координат (см. рис. 17, г), а в пространстве — в системах цилиндри­ческих (см. рис. 17, д) и сферических координат (см. рис. 17, е).

Векторный способ сводится к установлению расстояния точки от начала отсчета, а также направления радиуса-вектора (рис. 17, ж)1.