В искривленных скважинах

Для тела трубы условие прочности между растягивающими σ_р, МПа, и изгибающими σ_n ,МПа, напряжениями определяли согласно [1, с.94 ]

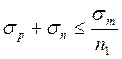, (10.42)

где n₁ =1,32 – запас прочности.

Растягивающие напряжения σ_р, Па, определяли согласно [1, с.92] по формуле

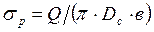, (10.43)

где Q – осевая растягивающая сила, обусловленная весом колонны

НКТ, Н.

Изгибающее напряжение σ_n , Па, определяли согласно [1, с.94] по формуле

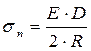, (10.44)

где Е – модуль упругости материала НКТ, Па, для стали Е=2,1·10¹¹ Па;

D – наружный диаметр трубы, м;

R – радиус искривления скважины, м.

Вопросы устойчивости колонны НКТ. Эффект Лубинского.

Колонны НКТ находятся под действием многообразных нагрузок, которые зависят от условий эксплуатации. Нагрузки эти в общем случае действуют как в продольном, так и в поперечном направлении.

Колонны НКТ можно представить как длинные, тяжелые трубчатые стержни. Поэтому как продольные, так и поперечные нагрузки при определенных условиях могут привести к потере устойчивости колонны и переходу ее в неустойчивое равновесное состояние, когда при малом отклонении от положения равновесия система не возвращается в исходное состояние силами упругости, а отклоняется на большую величину. В зависимости от характера нагружения колонна из исходного прямолинейного состояния переходит в изогнутую форму устойчивого равновесия, соответствующую минимуму потенциальной энергии системы или будут наблюдаться колебания колонны с увеличивающейся амплитудой. Потеря устойчивости наступает, когда нагрузки, действующие на колонну, достигают критических значений. Изгиб колонны с изменением формы равновесия при насосной добыче отмечен А. Лубинским.

Основной вид нагрузок при фонтанном и компрессорном способах добычи – силы собственного веса труб и давление газонефтяной смеси или сжатого воздуха (газа). Переменные нагрузки обусловлены периодическим изменением движущегося флюида или подаваемого воздуха.

Для свободно подвешенной колонны НКТ основным фактором, определяющим устойчивость колонны НКТ, является скорость движения жидкости в трубах. Если скорость флюида будет больше критической скорости, то произойдет потеря устойчивости нижнего участки колонны НКТ с переходом к режиму движения с возрастанием амплитуды колебания. Помимо скорости на устойчивость влияют внутреннее и наружное избыточные давления. Критическое избыточное наружное давление определяется по формуле

P_кр = 2,2 ·E·k²·k_min·ρ;

k = s₀/D;

k_min = s_min/D;

ρ = s₀/s_min;

s_min = 0,875·s;

s₀ = 0,905·s,

где s – толщина стенки трубы;

s₀,s_min – толщина стенки с учетом ее овальности;

D – наружный диаметр трубы;

Е – модуль упругости материала труб.

Колонна, закрепленная в пакере, может потерять устойчивость в процессе эксплуатации под влиянием давления, скорости движения флюида, температуры, в результате чего произойдет изгиб нижнего участка колонны с переходом к новым формам равновесия.

При ШСНУ-эксплуатации кроме статических нагрузок на колонну труб действую переменные усилия, связанные с переменным воздействием на колонну веса жидкости в трубах и сил трения плунжера насоса и штанг. При ходе плунжера вниз колонна вытягивается, при ходе плунжера вверх может произойти потеря устойчивости колонны с образованием ряда полуволн и закручиванием НКТ. Чем больше глубина подвески насоса, тем больше искривление колонны. Для предотвращения этого явления одной из мер является применение тяжелого низа колонны или ее заякоривание.

Заключение

От надежности работы НКТ во многом зависит успех разработки месторождения. НКТ является связующим звеном между глубинным и поверхностным оборудованием. При выборе того или иного типа НКТ необходимо четко определиться с составом откачиваемого флюида, глубиной скважины, знать профиль скважины. В зависимости от выбранного типа НКТ провести прочностные расчеты колонны от действия на нее нагрузки (собственный вес, давление, коррозия, искривление тела трубы, потеря устойчивости).

Список использованных источников

1 Сароян А.Е., Субботин М.А. Эксплуатация колонн насосно-компрессорных труб. - М.: Недра, 1985. – 216 с.

2 Трубы нефтяного сортамента: Справочник / Под общ. ред. А.Е.Сарояна. - М.: Недра, 1987. – 488 с.

Лекция 10.4

Введение

В настоящее время самыми распространенными установками для эксплуатации нефтяных скважин являются штанговые скважинные насосные установки (ШСНУ). Последние занимают две трети всего объема эксплуатационного оборудования, предназначенного для добычи пластовой жидкости. Одним из основных видов оборудования ШСНУ является привод штангового насоса, служащий для преобразования вращательного движения вала электродвигателя в возвратно-поступательное движение точки подвеса штанг (ТПШ).

Основная часть

ШСНУ состоит из привода, устьевого оборудования, колонны насосных штанг, колонны НКТ, непосредственно самого штангового насоса. Штанговый насос может быть вставным или невставным.

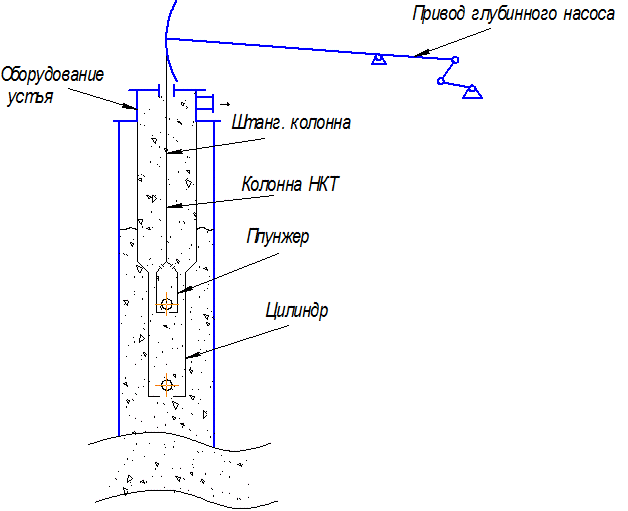Рисунок 10.21 – Схема ШСНУ с приводом в виде станка-качалки и

невставным штанговым насосом

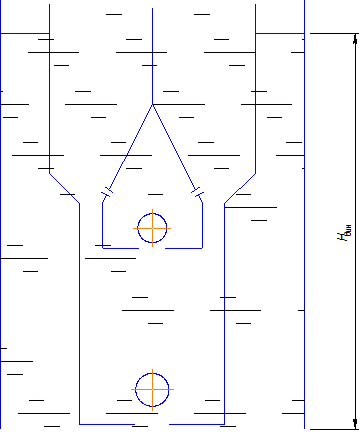
Рисунок 10.22 – Схема штангового скважинного вставного насоса

Вставной насос крепится на трубах НКТ с помощью замковой опоры. Насос может крепиться на верхней или нижней замковой опоре. Прием штангового насоса, как правило, оборудуется приемным фильтром (труба с отверстиями), газовым или песочным якорем. За рубежом нижняя часть подвески НКТ закрепляется с помощью якоря.

Колонна штанг зачастую оборудуется центраторами для уменьшения износа штанг и НКТ в наклонно-направленных скважинах и для борьбы с парафином (устанавливаются скребки).

Передаточный механизм штангового скважинного насоса с источником энергии называется приводом скважинного насоса. Привод ШСНУ выполняет следующие функции:

1) преобразование вращательного движения вала двигателя в возвратно-поступательное движение точки подвеса штанг (ТПШ);

2) снижение скорости вращения (числа оборотов) вала двигателя до числа двойных ходов ТПШ;

3) уравновешивание установки;

4) пуск и остановка ШСНУ;

5) регулирование режима откачки жидкости за счет изменения длины хода и числа ходов ТПШ;

6) контроль работы скважинного насоса динамометрированием.

Приводы ШСНУ могут быть классифицированы по роду используемой энергии в передаче, по числу обслуживаемых одним приводом скважин, по виду первичного двигателя.

В механическом приводе скважинного насоса основные функции выполняют механические передачи. В качестве передаточного звена в гидравлических приводах применяются жидкости, а в пневматических – воздух. Наиболее распространенными являются механические приводы ШСНУ.

Любой привод насоса имеет первичный двигатель, в качестве которого применяются электрические или тепловые двигатели. Электрические двигатели питаются от промысловой электроэнергии. Роль теплового двигателя выполняют двигатели внутреннего сгорания, работающие на жидком топливе, или газовые двигатели, работающие на промысловом газе.

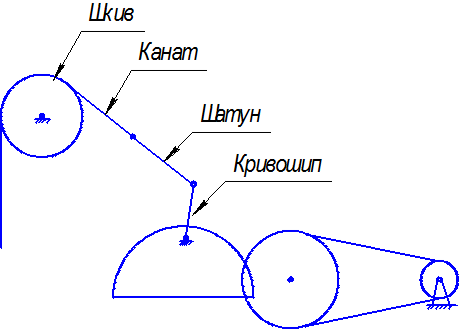
Рисунок 10.23 – Схема механического безбалансирного привода

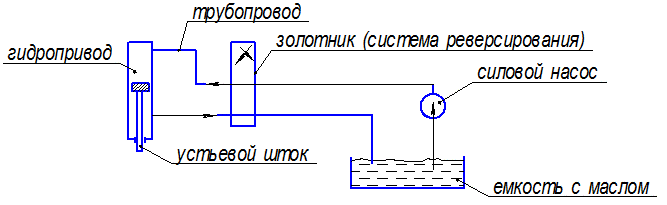Рисунок 10.24 – Схема гидравлического привода

Достоинства и недостатки:

1) механический привод более дешев и более доступен по сравнению с гидравлическим приводом, однако получаемый закон движения ТПШ несовершенен для работы штангового скважинного насоса. Желательно обеспечить равномерное движение плунжера.

2) гидропривод сложен в обслуживании, особенно зимой, имеет большую высоту, малоустойчивый. Однако с помощью гидропривода можно получить наиболее благоприятный закон движения ТПШ. Вместе с тем гидропривод не требует большого пространства около скважины, установки фундамента, т.к. крепится прямо на колонной головке. Гидроприводом легче реализуются групповые схемы эксплуатации нескольких скважин.

Наибольшее распространение получили индивидуальные механические приводы. Они классифицируются следующим образом:

1) по типу преобразующего механизма (балансирные и безбалансирные);

2) по величине максимальной нагрузки в ТПШ

- легкие Р_max≤30 кН;

- средние 30<Р_max≤100 кН;

- тяжелые Р_max>100 кН

3) по длине хода ТПШ

- короткоходовые S_max≤1 м;

- среднеходовые 1<S_max≤3 м;

- длинноходовые 3<S_max≤6 м;

- сверхдинноходовые S_max>6 м

4) по числу двойных ходов ТПШ

- тихоходовые n_max≤6;

- среднее число ходов 6<n_max≤15;

- быстроходные n_max>15

5) по потребляемой мощности

- маломощные N_max≤5 кВт;

- средней мощности 5<N_max≤25 кВт;

- мощные 25<N_max≤100 кВт;

- сверхмощные N_max>100 кВт.

В балансирном приводе вертикальное возвратно-поступательное движение ТПШ осуществляется посредством качающегося балансира (коромысла), а в безбалансирных приводах механического действия это движение осуществляется механизмами без применения качающегося балансира (рисунок 10.23).

Балансирный индивидуальный привод называют станком-качалкой.. Помимо вышеизложенных параметров индивидуальные механические приводы характеризуются еще и максимальным крутящим моментом на ведомом валу редуктора трансмиссии (приводы с малым моментом, со средним, с большим и со сверхбольшим). Приближенная зависимость между моментом М, нагрузкой Р и ходом S ТПШ выглядит так:

М_мах ≈ (1/8÷1/6) Р_max · S_max.

Cуществуют многочисленные конструкции станков качалок, выполненные по различным кинематическим схемам как трансмиссии, так и преобразующего механизма.

Балансиры станков-качалок на практике встречаются двух видов: как механизм двуплечего рычага (рычаг первого рода), так и механизм одноплечего рычага (рычаг второго рода).

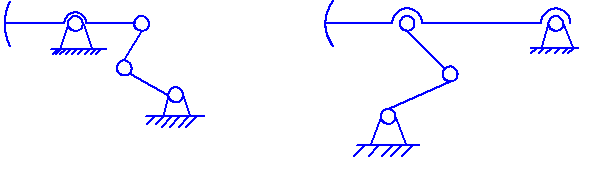
Рисунок 10.25 – Схемы балансиров станков-качалок

По способу уравновешивания станки-качалки бывают четырех типов: балансирные, кривошипные (роторные), балансирно-кривошипные (комбинированные), шатунные.

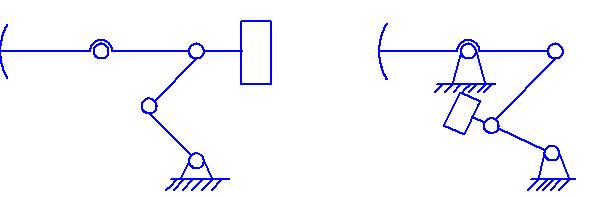
Рисунок 10.26 – Схемы размещения уравновешивающих грузов

станков-качалок

По месту расположения кривошипного центра можно различить три вида станков-качалок (рисунок 10.27, а-в).

Из рисунка 10.27 видно, что при помощи этих трех преобразующих механизмов, имеющих общий балансир ВСD, получается один и тот же угол размаха δ₀ и длина хада ТПШ S₀=K₁·δ₀. Принципиально они отличаются тем, что средняя скорость ТПШ в каждом полуцикле (ход вверх и вниз) разная.

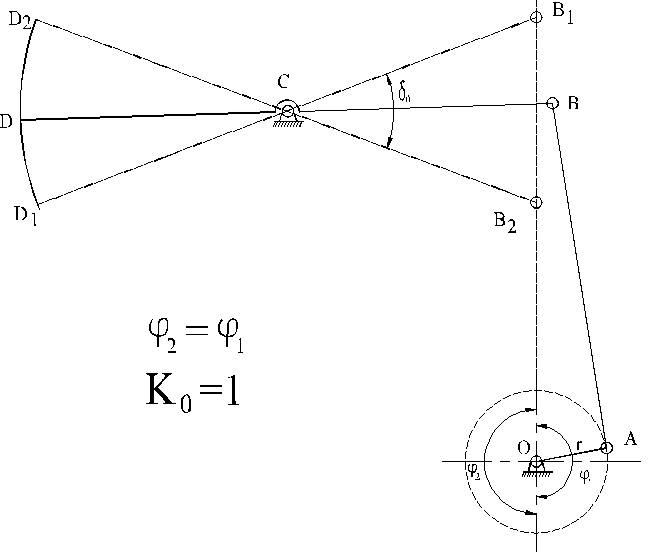
Рисунок 10.27 (а) – Станок-качалка аксиальный (нормального ряда)

Аксиальный механизм OABCD с расположением кривошипного центра О на прямой В₁В₂ представлен на рисунке 10.27, а. Время хода вверх и вниз одинаково независимо от направления вращения кривошипа. Это станок-качалка нормального ряда.

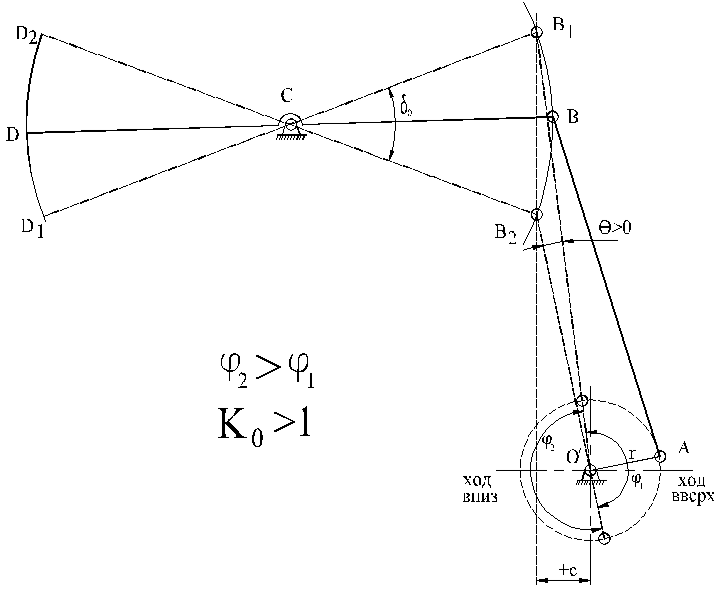
Рисунок 10.27 (б) – Станок-качалка дезаксиальный

(дезаксиал положительный)

Дезаксиальный станок-качалка с положительным дезаксиалом представлен на рисунке 10.27, б. При вращении кривошипа по часовой стрелке (устье слева) ход вверх происходит быстрее хода вниз. При вращении кривошипа против хода часовой стрелки наоборот ход вверх по времени занимает больше времени, чем ход вниз.

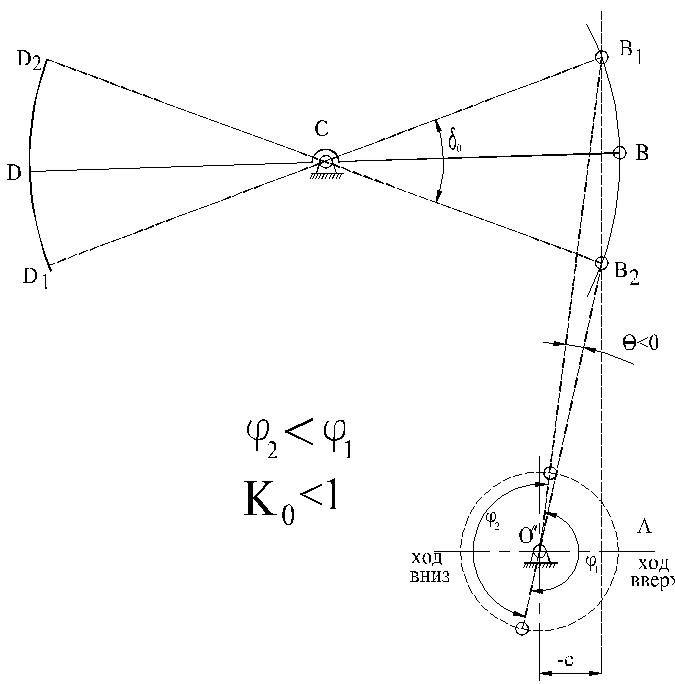
Рисунок 10.27 (в) – Станок-качалка дезаксиальный

(дезаксиал отрицательный)

Дезаксиальный станок-качалка с отрицательным дезаксиалом представлен на рисунке 10.27, в. При вращении кривошипа по часовой стрелке ход вверх происходит медленнее хода вниз и наоборот, при вращении кривошипа против хода часовой стрелки ход вверх происходит быстрее хода вниз.

Если кривошип ОА вращается с постоянной угловой скоростью, то отношение углов поворота φ₁ и φ₂ равно

φ₁/φ₂ = t₁/t₂,

где t₁, t₂ – время хода вверх и вниз соответственно.

За время t₁ и t₂ ТПШ пройдет пути, равные дугам

D₁D₂ = D₂D₁ = S₀ = K₁·δ₀.

Тогда средняя скорость при ходе вверх и вниз равны v₁= S₀/t₁ и v₂= S₀/t₂.

Следовательно v₁/v₂ = t₂/ t₁ = φ₂/φ₁ = К₀.

Для положительного дезаксиала подставляя значения углов

φ₁ =180º - Θ;

φ₂ = 180º + Θ;

К₀ = (180º + Θ) / (180º - Θ);

Θ = (К₀ – 1) / (К₀ + 1)·180º,

где К₀ – коэффициент изменения средней скорости ТПШ.

Для аксиального механизма угол Θ=0.

Достоинства и недостатки рассмотренных кинематических схем.

ТПШ при ходе вверх нагружена больше, чем при ходе вниз. Вместе с тем ТПШ движется неравномерно, с ускорением. Следовательно инерционные нагрузки при ходе вверх больше инерционных нагрузок при ходе вниз. Для того, чтобы снизить инерционные составляющие нагрузки ТПШ при ходе вверх, нужно уменьшить абсолютные значения ускорения при ходе вверх. Абсолютные значения ускорения ТПШ при ходе вврех можно уменьшить, уменьшив среднюю скорость хода ТПШ вверх, т.е. применить станок-качалку с отрицательным дезаксиалом при вращении кривошипа по часовой стрелке или с положительным дезаксиалом при вращении кривошипа против вращения часовой стрелки.

Вращение кривошипа против часовой стрелки не всегда выгодно, поэтому для уменьшения ускорения ТПШ при ходе вверх применяются станки-качалки с отрицательным дезаксиалом. За рубежом нашли применение станки-качалки с положительным дезаксиалом.

Выбор станка-качалки, кроме всего прочего, зависит и от свойств откачиваемой жидкости. Если зазор между плунжером и цилиндром большой, при большом времени подъема жидкость просачивается вниз, уменьшая тем самым КПД насоса. Напротив, неоправданно большой отрицательный дезаксиал повышает вероятность зависания колонны штанг в трубах при ходе вниз за счет большой скорости спуска, особенно при ее работе в наклонно-направленных скважинах и скважинах с отложениями парафина или гидратов.

Обозначение станков-качалок

ГОСТ 5866-76

СК5-3-2500

5 – максимальная нагрузка на устьевой шток, т (50 кН)

3 – максимальная длина хода ТПШ, м

2500 – наибольший допускаемый крутящий момент на ведомом валу редуктора, кН·м, увеличенный в 100 раз (25 кН·м)

Одноплечные станки-качалки

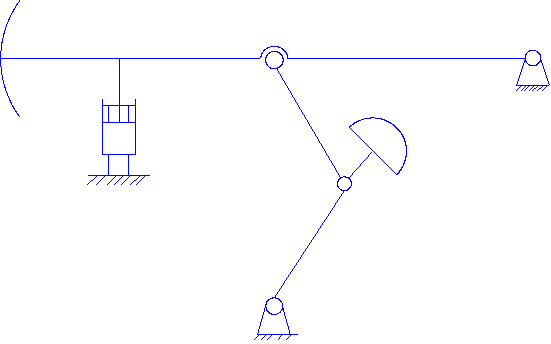
Рисунок 10.28 – Одноплечный станок-качалка

Зарубежным производителем одноплечных станков-качалок является фирма Lufkin (США), выпускающая станки типа MARK I, MARK II (см. рисунок 10.25, 10.28). В России одноплечные станки-качалки выпускает Уралтрансмаш (г. Екатеринбург) – привод ПШГНО 6-2,5.

Достоинства и недостатки:

1) они более компактны, имеют меньшую металлоемкость, имеют более лучший подходящий закон движения ТПШ, позволяющий уменьшить динамическую составляющую нагрузки на 10-12 %;

2) имеют малую боковую устойчивость (большая высота при малой ширине), что повышает требования к фундаменту;

3) кривошипы и уравновешивающие грузы находятся в опасной близости от устья, что затрудняет ремонтные работы.

Подобные станки-качалки выпускают только большой грузоподъемности ТПШ (20 т и выше) и когда фактор компактности играет решающее значение. Зачастую у данных станков применяется гидропневматическое уравновешивание, что позволяет избавиться от грузов на кривошипе.

Заключение

Привод штанговых скважинных насосов в работе всей системы ШСНУ играет решающее значение. От его работы зависит не только транспортирование пластовой жидкости к устью скважины, но и оптимальные кинематические и динамические составляющие, дающее возможность с минимальными затратами производить эксплуатацию скважин. Существуют приводы первого и второго рода, имеющие свои достоинства и недостатки. Привод станка-качалки требует особого внимания, особенно в зимние периоды работы.

Список использованных источников

1. Молчанов Г.В., Молчанов А.Г. Машины и оборудование для добычи нефти и газа. Учебник для вузов. – М.: Недра, 1984. – 464 с.

2. Чичеров Л.Н. Нефтепромысловые машины и механизмы. - М., Недра, 1983. – 308 с.

Лекция 10.5

Введение

Для нормальной работы штангового скважинного насоса необходимо ТПШ станка-качалки обеспечить равномерное гармоничное движение, без ускорений. В реальности закон движения ТПШ отличается от гармонического. С целью выявления реального закона движения ТПШ необходимо рассмотреть кинематику движения четырехзвенного механизма станка-качалки.

Основная часть

При проектировании станков-качалок, при расчете нагрузок, действующих на штанговую колонну, необходимо знать законы изменения перемещения, скорости и ускорения ТПШ в зависимости от угла поворота кривошипа и в зависимости от геометрических параметров станка-качалки (соотношение длин станка-качалки). Преобразующий механизм станка-качалки представляет собой четырехзвенник ОАВСД (рисунок 10.29).

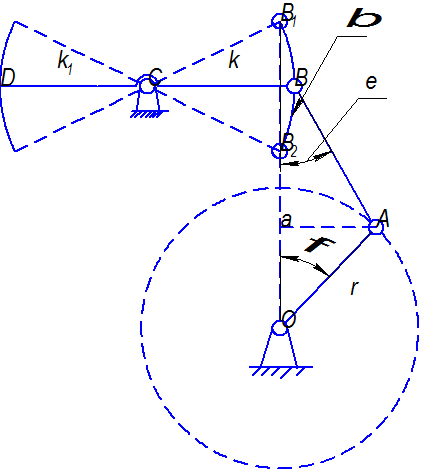
Рисунок 10.29 – Схема к определению закона перемещения, скорости

и ускорения ТПШ станка-качалки

В настоящее время в зависимости от принятых допущений различают три основных способа определения закона движения ТПШ:

1 способ – элементарная теория

Подразумевается, что т.В движется по прямой, угол β=0.

Это достигается, если r/l=0; r/k=0.

2 способ – приближенная теория

Снимаются некоторые допущения r/k=0, r/l≠0, т.е. учитывается угол β.

3 способ – точная теория

Признается конечная длина элементов и т.В движется по дуге.

Для промысловой практики достаточную точность обеспечивает приближенная теория.

Длина пути S_В, пройденная т.В при повороте кривошипа на угол φ, равна отрезку В₁В

S_В= В₁В=ОВ₁-ОВ;

ОВ₁=r+l;

ОВ=Oa+aB;

ОВ=r·cos φ + l·cos β

Окончательно

S_В= r+l-(r·cos φ + l·cos β)= r- r·cos φ+l-l·cos β= r(1- cos φ)+l(1-cos β).

По теореме синусов для треугольника ОАВ следует

r/sin β= l/sin φ;

sin β=r/l · sin φ;

т.к.

S_В=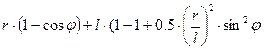

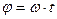
S_В=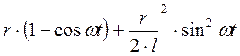

Искомое перемещение т.Д определится исходя из перемещения т.В с учетом соотношения плеч балансира К₁/К

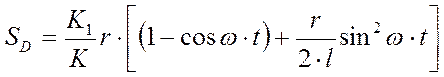(1)

где ω – угловая скорость вращения кривошипа.

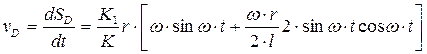
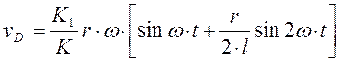(2)

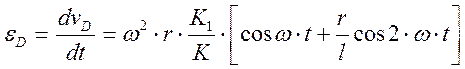(3)

Анализ полученных зависимостей показывает, что максимальный путь т.D пройдет при перемещении кривошипа на угол φ=ωt=180º.

S_Dmax=2·r·K₁/K

Максимальная скорость будет при углах поворота кривошипа ωt=90º=270º.

V_Dmax=±ω·r·K₁/K=±ω·S_Dmax/2.

Максимальное ускорение будет при ωt=0º=180º

ε_Dmax= .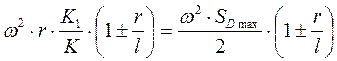

Уравнения (1)-(3) описывают закон движения ТПШ при допущении, что траектория движения т.В – прямая. Если пренебречь также и величиной отношения r/l, как это принимается в элементарной теории, то из полученных зависимостей после подстановки r/l=0 получим следующее:

.

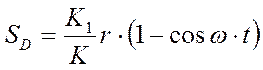
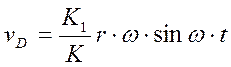
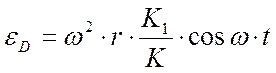Из анализа этих зависимостей следует, что для балансирного станка-качалки, у которого длина радиуса кривошипа мала по сравнению с длиной шатуна и балансира, закон движения ТПШ является гармоническим.

Гармонический закон движения ТПШ – своеобразный эталон, с которым сравнивают фактические законы движения ТПШ, отличающиеся от гармонического в силу конечных длин элементов преобразующего механизма и ряда других факторов, например, неравномерности вращения кривошипа.

Таким образом, даже при анализе приближенных формул можно убедиться, что закон движения ТПШ отличается от гармонического в сторону увеличения максимальных ускорений. При чем это отличие тем больше, чем больше соотношение r/l.

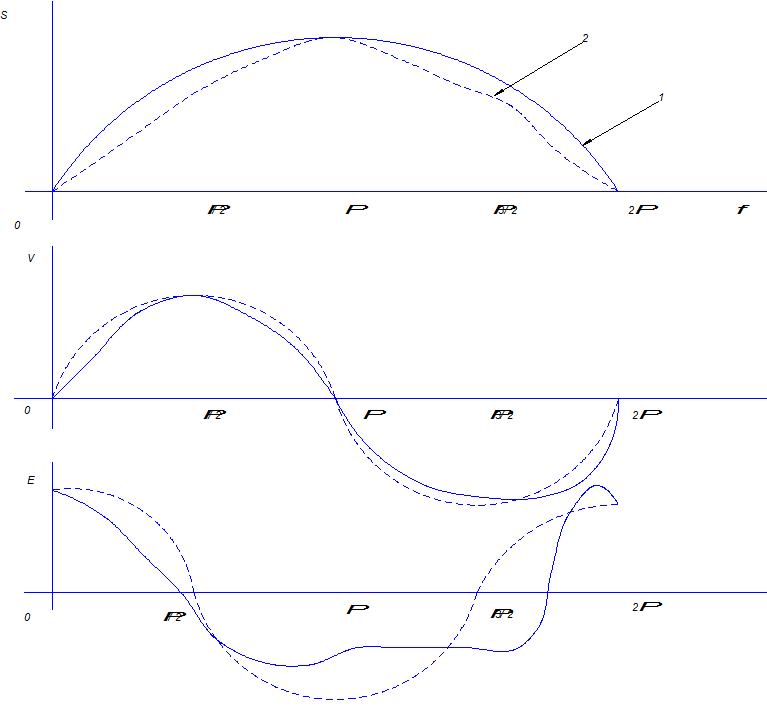
1- упрощенная методика; 2 – идеальный гармонический закон

Рисунок 10.30 – Графические зависимости закона изменения

перемещения, скорости и ускорения ТПШ при

гармоническом и реальном движении

Кинематические показатели станков-качалок

Для нормальной работы штангового скважинного насоса желательно обеспечить движение ТПШ по гармоническому закону. При проектировании станков-качалок учитывается конечная длина элементов качалки, в результате чего закон движения ТПШ отличается от гармонического.

На увеличение ускорений ТПШ значительно влияет четырехзвенник. Это существенно сказывается на работоспособности штанг и упругих узлов установки. Ускорение ТПШ минимальное при гармоническом колебательном движении штанг. Таким образом, станок-качалка является с точки зрения кинематики движения несовершенным.

Первым критерием совершенства станка-качалки можно назвать отношение наибольшего реального ускорения к ускорению при гармоническом движении:

m = ε_Dmax/ε_Dгарм.

Коэффициент m называют кинематическим коэффициентом станка-качалки.

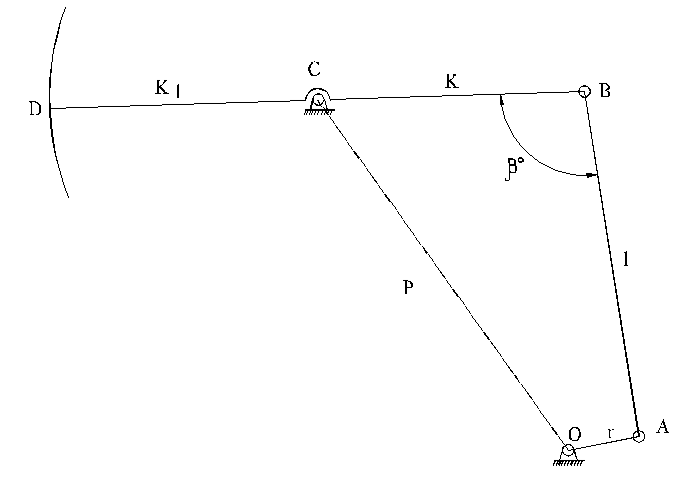
Рисунок 10.30 – Схема четырехзвенника станка-качалки

;

,

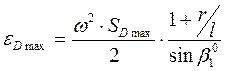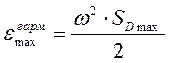где 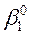- угол между балансиром и шатуном при крайнем верхнем положении т.В

m = 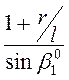- формула А.М. Пирвердяна

А.С. Аливердизаде выведена другая формула на основании точной теории

m = ,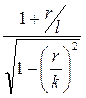

где r, l, k – размеры четырехзвенника.

Чем ближе значение m к единице, тем совершеннее станок-качалка. Исследования показали, что при m≤1,3 при негармоническом движении увеличение нагрузок практически незаметно по сравнению со станком-качалкой, дающей гармоническое движение штанг. При m>1,3 чуствуется резонанс второй гармоники, и уже при m>1,4 значительно растут усилия. Так, например, при m=1,4 и глубине подвески 1200 м инерционные усилия возрастают на 50 %, при этом возрастают и отрицательные тангенциальные усилия. Конечно, для меньших нагрузок и глубины подвески насоса кинематический коэффициент может быть большим. С другой стороны, снижение коэффициента m увеличивает габариты станка-качалки (при необходимой длине хода и величине r для уменьшения m приходиться увеличивать 1), повышает расход металла, ухудшает условия эксплуатации. Поэтому в мощных станках-качалках трудно соблюсти минимальную величину кинематического коэффициента. Рациональный кинематический коэффициент определяют с учетом всех факторов – изменения усилий, габаритов, металлоемкости. В частности при станке-качалке малой грузоподъемности (1СК, 3СК) увеличение инерционных сил по абсолютной величине незначительно, поэтому допустимы большие значения m, за счет чего сокращаются габариты.

Вторым критерием совершенства четырехзвенника является симметрия привода, симметрия изменения угла 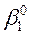относительно 90º. Это основное условие равного времени хода вверх и хода вниз. При сокращении времени хода вверх за счет времени хода вниз возрастают скорости и ускорения движения ТПШ вверх. Это вызывает увеличение динамических нагрузок на установку. Обратное распределение времени сокращает скорость хода вверх, увеличивает утечки в погружном насосе, наблюдается гидравлический удар при переходе к ходу вниз.

Несоблюдение симметрии приводит к возрастанию горизонтальных сил, действующих на поры балансира, шатуна. Поэтому надо стремиться к равенству

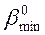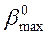90º - = - 90º

Это согласно теории механизмов и машин выражается равенством

l² +k² = r² + p² .

Заключение

Таким образом, из сказанного выше следует, что законы кинематики ТПШ в процессе работы являются негармоническими. Степень приближения реальной ТПШ к гармоническому колебанию характеризуется коэффициентом кинематического совершенства, величина которой определяется геометрическими параметрами четырехзвенника станка-качалки.

Список использованных источников

1. Молчанов Г.В., Молчанов А.Г. Машины и оборудование для добычи нефти и газа. Учебник для вузов. – М.: Недра, 1984. – 464 с.

2. Чичеров Л.Н. Нефтепромысловые машины и механизмы. - М., Недра, 1983. – 308 с.

Лекция 10.6

Введение

Рассмотренные в предыдущей лекции вопросы кинематики ТПШ говорят о негармоническом движении, что влечет за собой возникновение значительных вибрационных и инерционных усилий, осложняющих работу станка-качалки. Рассмотрим природу их возникновения и оценим их количественно.

Основная часть

Впроцессе работы штанговой скважинной насосной установки в точке подвеса штанг действуют нагрузки, которые можно раз­делить на

I. Постоянные (или статические) нагрузки:
вес колонны штанг в жидкости Р'_ш;

гидростатическая нагрузка Р_ж,обусловленная разницей дав­лений жидкости над и под плунжером скважинного насоса.

II. Переменные нагрузки:

инерционная нагрузка Р_и,обусловленная переменной по ве­личине и направлению скоростью движения колонны штанг;

вибрационная нагрузка Р_виб, обусловленная колебательными процессами в колонне штанг под действием ударного прило­жения и снятия гидростатической нагрузки Р_ж на плунжер;

силы трения, возникающие в результате взаимодействия ко­лонны штанг и насосно-компрессорных труб Р_трм, обтекания пластовой жидкостью колонны штанг Р_трг, взаимодействия плунжера и цилиндра скважинного насоса Р_трпл, перепада дав­ления в клапанах насоса Р_кл, обусловленного их гидравличе­ским сопротивлением.

В зависимости от характеристики скважины глубины под­вески насоса, диаметров его плунжера, колонны штанг и труб, длины хода штанг, числа качаний, вязкости пластовой жид­кости и т. п. доля указанных составляющих в общем балансе сил уменьшается. Все эти силы изменяются в течение одного цикла работы установки.

В общем виде усилия в точке подвеса штанг при ее ходе вверх Р_в и вниз Р_н будут:

Р_в=Р^/_ш+Р_ж+Р_ив+Р_вибв+Р_трм+Р_трг+Р_трпл+Р_клв ,

Р_н=Р^/_ш- (Р_ин+Р_вибн+Р_трм+Р_трг+Р_трпл+Р_клн) .

Деформации колонны штанг и насосно-компрессорных труб определяются особенностями приложения к ним нагрузки в различные фазы работы скважинного насоса. Рассмотрим взаимосвязь сил и перемещений, последовательно уменьшая число упрощающих допу­щений. (Во всех случаях будем счи­тать, что утечки в зазоре между плунжером и цилиндром, а также в клапанных узлах скважинного наcoca отсутствуют, а пластовая жид­кость дегазирована.)

На первом этапе рассмотрим ра­боту внутрискважинного оборудова­ния, полагая, что из всех ранее пе­речисленных сил действуют только вес штанг, погруженных в жид­кость, Р ^/_ш и гидростатическая на­грузка Р_ж.

Переменные нагрузки рассмат­ривать не будем, что допустимо при предположении, что точка подвеса штанг движется очень медленно; си­лами трения пренебрегаем. Примем также, что колонны штанг и труб не деформируются.

В этом случае динамограмма скважинного насоса, т. е. гра­фическая зависимость усилия в точке подвеса штанг D от ее перемещения (рисунок 10.31, а) будет представлять собой прямо­угольник ABCD, площадь которого равна полезной работе, со­вершаемой при подъеме пластовой жидкости. Во время хода штанг вверх усилие в точке подвеса штанг будет соответство­вать ординатам точек В и С и равно Р'_ш + Р_ж при ходе штанг вниз оно будет соответствовать ординатами точек D и А и равно Р'_ш. Таким образом, полученная динамограмма напоми­нает простейшую индикаторную диаграмму поршневого насоса.

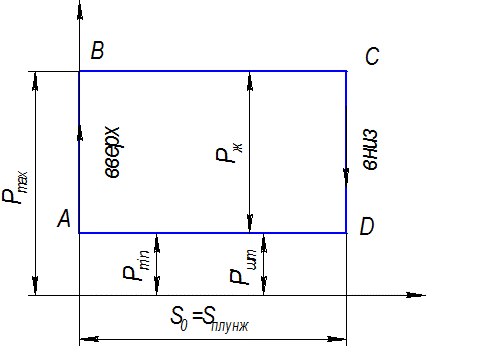
Рисунок 10.31, а – Идеальная динамограмма работы ШСНУ

Однако работа скважинной насосной установки сопровож­дается значительными периодическими удлинениями колонны штанг λ_ш и труб λ_т (рисунок 10.31, б).

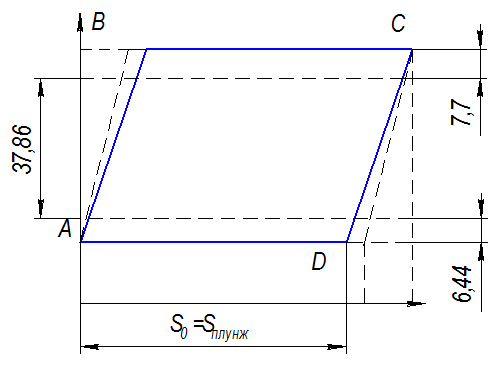
Рисунок 10.31, б – Динамограмма работы ШСНУ с учетом упругих

деформаций штанг и труб

В начале хода штанг вверх, т. е. в конце предыдущего цикла работы насоса, точка подвеса штанг и плунжер нахо­дятся в нижнем положении точки А'. При этом нагнетательный и всасывающий клапаны закрыты. При перемещении усть­евого штока вверх колонна штанг воспринимает усилие от веса столба жидкости и под ее действием начинает растягиваться, одновременно с этим по мере восприятия штангами ко­лонна НКТ разгружается и, следовательно, сжимается. В тече­ние периода передачи усилия веса столба жидкости от труб штангам плунжер и цилиндр двигаются вверх (на величину λ_т), не перемещаясь относительно друг друга. Когда устьевой шток переместится вверх на расстояние, равное сумме абсо­лютных деформаций штанг λ_ш и труб λ_т под действием веса столба жидкости Р_ж (что будет соответствовать точке Д'), плунжер начнет двигаться относительно цилиндра. Если бы скважинный насос был заякорен, т. е. жестко закреплен отно­сительно эксплуатационной колонны, то восприятие нагрузки колонной штанг характеризовалось бы прямой А'b^/.

Поскольку к колонне штанг приложены также и силы меха­нического и гидродинамического трения R_B, то ордината точки, соответствующей окончанию процесса деформирования штанг, возрастает на их величину.

После окончания деформирования штанг и труб плунжер на­чинает двигаться вверх (участок В'С^/), всасывающий клапан открывается, и пластовая жидкость заполняет объем под плун­жером насоса.

Максимальная нагрузка в точке подвеса штанг при ходевверх будет определяться суммой P_maxb = Р^/_ш + Р_ж+ R_в.

Достигнув верхней крайней точки, устьевой шток останав­ливается (точка С^/) и начинает перемещаться вниз (линия C ^/D'). При этом всасывающий клапан закрывается, а нагнета­тельный открывается. В результате усилие от веса столба жид­кости над плунжером насоса Р_ж начинает по мере движения устьевого штока вниз переноситься со штанг на трубы, что бу­дет сопровождаться сжатием штанг и растяжением труб. До окончания этого процесса плунжер будет неподвижен относи­тельно цилиндра, и лишь когда последний сместится вниз на величину λ_т, а колонна штанг сожмется на величину λ_ш (точка D'), плунжер начнет двигаться относительно цилиндра. Точка д^/ соответствует циклу работы насоса с заякоренным цилинд­ром.

Во время движения плунжера вниз относительно цилиндра нагнетательный клапан открыт, нагрузка в точке подвеса штанг постоянна и равна Р_minн = Р'_ш – R_н, так как силы трения на­правлены в сторону, противоположную движению штанг.

Цикл работы скважинного насоса заканчивается при под­ходе плунжера к нижнему положению, где он останавлива­ется, - точка А^/. Далее процесс повторяется.

Усилия, действующие в описанном цикле работы, состав­ляют:

вес колонны штанг, погруженной в жидкость:

,

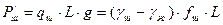где q_ш - масса 1 м штанг в откачиваемой жидкости, L — глу­бина подвески насоса, λ_ш, λ_ж - удельный вес материала штанг и пластовой жидкости, f_ш - средняя площадь поперечного се­чения колонны штанг.

Вес столба жидкости над плунжером скважинного насоса

Р_ж = F_пл · γ_ж · (L – h) = F_пл· γ_ж ·H=q_ж·Н·g ,

где F_пл - площадь поперечного сечения плунжера, γ_ж - удель­ный вес откачиваемой жидкости, h - погружение насоса под ди­намический уровень, Н - высота подъема жидкости, q_ж - масса 1 м столба жидкости над полной площадью поперечного сечения плунжера.

Несложно доказать, что при подсчете сил, действующих на балансир, можно считать вес штанг без учета архимедовой силы, но тогда давление жидкости следует считать действующим на кольцевое сечение площади плунжера за вычетом площади сечения штанг. Если же принимать вес штанг с учетом потери веса в жидкости, то давление следует брать на полную площадь плунжера.

Сила механического трения колонны штанг о НКТ зависит от большого числа факторов: диаметра штанг и муфт, коэффи­циента трения, продолжительности совместной работы колонны штанг и НКТ, инклинограммы скважины и ряда других факто­ров, а поэтому точное определение их довольно сложно.

Как показывают длительные наблюдения, для скважин с не­большим искривлением их величина составляет 2—5 % от ста­тических сил.

Для определения сил трения штанг может быть использо­вана приближенная формула

,

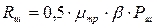где μ_тр - коэффициент трения между штангами и трубами, мак­симальное значение которого принимают 0,25 - 0,3; β- угол отклонения оси скважины от вертикали, рад.

Сила трения плунжера о цилиндр может быть найдена с по­мощью эмпирической формулы.

Р_н = ,

где D_пл - диаметр плунжера, м; δ - зазор, мм; коэффициенты т₁ и т₂ принимают значения для обводненных скважин 1,84 и 137, для безводных— 1,65 и 127 соответственно.

Силы гидродинамического трения, обусловленные обтека­нием колонны штанг и ее муфт жидкостью, могут изменяться в широких пределах в зависимости, прежде всего, от скорости относительного перемещения и вязкости пластовой жидкости. Для маловязких нефтей они незначительны и изменяются в пре­делах 200 - 500 Н, для высоковязких — соизмеримы с весом ко­лонны штанг.

Длина хода плунжера относительно цилиндра скважинного насоса представляет собой разность хода точки подвеса штанг и упругих удлинений колонны штанг и труб под действием столба жидкости Р_ж.

Абсолютные упругие удлинения штанг и труб соответственно

,

,

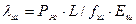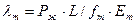где f_ш, f_т - площадь поперечного сечения тела штанг и труб соответственно, Е_ш, Е_т - модуль упругости материала штанг и труб соответственно.

Тогда длина хода плунжера S_пл будет определяться по фор­муле

S_пл = S₀ – (λ_ш – λ_т),

где S₀ - длина хода точки подвеса штанг.

В рассмотренном процессе работы внутрискважинного обо­рудования инерционные усилия, обусловленные неравномерным движением точки подвеса штанг, не рассматривались.

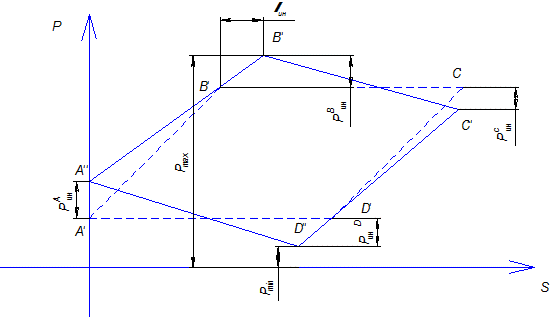
Рисунок 10.31, в – Динамограмма работы ШСНУ с учетом упругих

деформаций штанг и труб и инерционных усилий

Дополнительные инерционные силы для отдельных фаз ра­боты будут состоять из (рисунок 10.31, в):

дополнительной нагрузки, обусловленной разгоном колонны штанг в начале их хода вверх,

Р_А^//_и = Р_ш·w_А^//·k_w/g ,

где w_А^// - ускорение точки подвеса штанг в начале хода, k_w — коэффициент, учитывающий закон изменения ускорения по дли­не колонны (k_w ≈0,5);

силы, обусловленные инерцией столба жидкости в момент окончания деформации штанг в точке подвеса,

Р_жи = Р_ж∙ w_В^//_ж/g.

Так как ускорение столба жидкости отличается отускоре­ния плунжера вследствие разных площадей поперечного сече­ния столба жидкости в трубах F_т-f_ш и эффективной площади поперечного сечения плунжера f_пл-f_ш, то выразим Р_жисле­дующим образом:

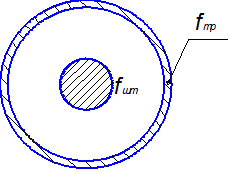
Для удобства дальнейших преобразований умножим числи­тель и знаменатель дроби на Р_ш. После преобразования полу­чим

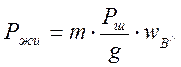
где m=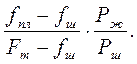

Для упрощения расчетов принимают w_B^/ = w_B^//.

В результате максимальное усилие будет Р_max = P_cт+Р_ши+Р_жи или

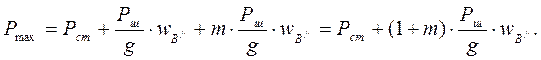
С помощью аналогичной формулы можно выразить усилия, действующие в период В^//-С^// движения точки подвеса штанг, при этом вместо w_В^// должно быть подставлено текущее значение w.

Особенностью изменения усилия в период В^//-С^// будет уменьшение w от максимального до нуля и далее, переход его в область отрицательных значений. Усилие, действующее при этом, также будет уменьшаться, и кривая В^//С^// пересечет В^/С^/ и достигнет значения

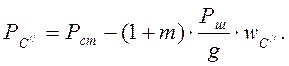
При ходе вниз штанги начинают деформироваться. В момент окончания деформации штанг и труб усилие в точке подвеса будет составлять

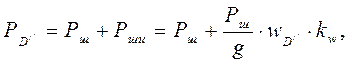
где w_D^// - ускорение точки подвеса штанг в конце упругой деформации штанг и труб при ходе вниз.

При этом упругое сокращение колонны штанг будет

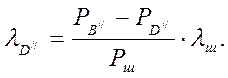
Во время дальнейшего движения штанг вниз в точке подвеса будет действовать постоянное усилие от веса штанг Р_ш и переменное от силы инерции

Рассмотренная картина изменения усилий и перемещений точки подвеса штанг не учитывала дополнительных инерцион­ных нагрузок, связанных с возникновением в колонне штанг упругих колебаний в момент приложения к колонне штанг веса столба жидкости.

На колонну штанг в течение двойного хода действуют два импульса от веса столба жидкости, расположенной над плун­жером насоса. Первый импульс действует при начале хода плунжера вверх, когда нагнетательный клапан закрывается, и нагрузка Р_ж воспринимается колонной штанг. Второй импульс действует при ходе вниз, когда нагнетательный клапан открывается, и нагрузка Р_ж передается на колонну НКТ

Время приложения и снятия силы Р_ж мало по сравнению с периодом собственных колебаний колонны, а поэтому для оп­ределения дополнительных сил можно использовать теорию, описывающую продольные колебания при ударе по призмати­ческому стержню. Общие положения этой теории были разра­ботаны Б. Сен-Венаном, и для решения рассматриваемой за­дачи использованы А. С. Вирновским.

Рассмотрим стержень большой протяженности, закреплен­ный в точке х = 0абсолютно жестко. Если к его свободному торцу приложить возмущение и(х=1,t), дающее продольное смещение этого торца во времени, то очевидно, что перемещение какого-либо сечения стержня будет зависеть как от координаты этого сечения х, так и от времени t.

Таким образом, смещение любого сечения будет функцией двух переменных: и= и(х, t).

Рассмотрим элемент стержня длиной Δх (рисунок 10.32), нахо­дящийся на расстоянии х от верхнего закрепленного торца. Масса этого элемента Δm = ρFΔx,где ρ, F - соответственно плотность материала и площадь поперечного сечения.

Спроектировав все силы (в том числе и силу инерции), дей­ствующие на элемент Δх,на вертикаль, получим

где q - вес единицы длины стержня. Знак приближенного ра­венства здесь поставлен потому, что предполагается постоянство ускорения д²и/ дt² на длинеΔх, что в действительности не имеет места.

Выразим усилие N через напряжения, действующее в этих сечениях, и, подставив значение Δm, получим

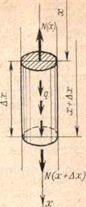
Рисунок 10.32 – Элемент колонны штанг

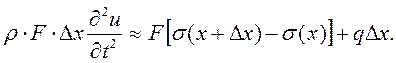
Упростив выражение и учтя, что напряжения меняются во времени, получим

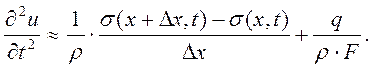
Перейдя к пределу Δх→0, становится возможным получить точное равенство, справедливое для сечения с координатой х:

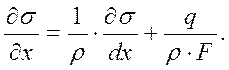
Полагая, что деформация колонны штанг связана с напря­жениями функцией σ = и(ε), запишем:

Так как деформация ε представляет собой частную произ­водную от смещения и по х, т. е. ε=ди/дх,

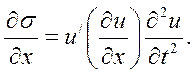
Поскольку деформации материала штанг при работе их в нормальных условиях подчиняются закону Гука, то

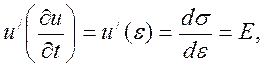
где Е - модуль упругости первого рода.

Подставив это в полученное уравнение, будем иметь

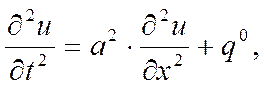
где , ,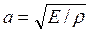

где а - скорость распространения звука в металле. Полученное уравнение называется волновым.

Продольные перемещения стержня, описываемые волновым уравнением, представляют собой сумму статических смеще­ний, обусловленных слагаемым q°, и динамического смещения, обусловленного компонентой .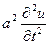

В соответствии с принципом суперпозиции рассчитаем ди­намическое смещение, поскольку только оно определяет допол­нительную динамическую составляющую.

Поэтому в дальнейшем будем рассматривать волновое урав­нение в виде

При определении дополнительной динамической составляю­щей будем считать верхнюю точку колонны штанг неподвиж­ной и закрепленной, а к нижнему торцу будет приложено уси­лие от веса столба жидкости. Дополнительная динамическая нагрузка будет обусловлена напряжениями, распространяющи­мися в виде упругой волны от плунжера к точке подвеса штанг.

Граничные условия для колонны штанг на закрепленном конце: и = 0 при любом t, х = 0.

Отсчитывая упругие перемещения, обусловленные волновым процессом, от равновесных положений сечений штанги, соот­ветствующих моменту начала движения плунжера относительно цилиндра, можно записать u=0, 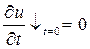для любого х.

Скорость всех сечений колонны штанг в конце периода на­чальных деформаций будем считать изменяющимися по линей­ному закону. Тогда для произвольного сечения в начальный мо­мент времени

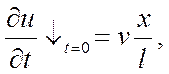
где v – скорость плунжера относительно точки подвеса штанг.

Граничное условие для нижнего конца колонны может быть получено исходя из силы инерционного движения жидкости. Не учитывая сжимаемости жидкости, можно записать

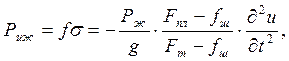
где Р_ж=γ_ж∙(F_пл – f_ш)∙L – вес жидкости над плунжером скважинного насоса.

Так как 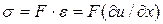, то с учетом обозначения

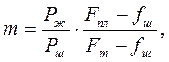
где Р_ш = γ_ш∙f_ш∙L получим

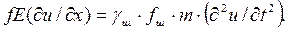
Отсюда граничное условие для нижнего конца штанг можно представить в виде

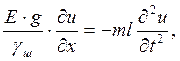
так как 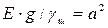, то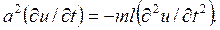

Интегрирование волнового уравнения при перечисленных граничных условиях дает величину дополнительного напряжения в точке подвеса штанг

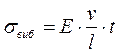при 0 < t < l/a,

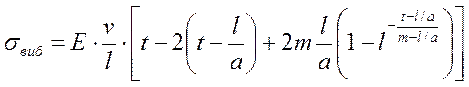
при l/a < t <3( l/a).

Максимальное напряжение будет в период времени l/a < t <3( l/a):

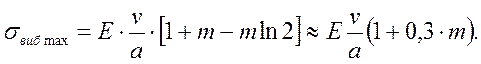
Подставив в полученное выражение скорость плунжера от­носительно точки подвеса в момент окончания периода началь­ных деформаций

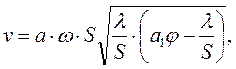
получим дополнительную инерционную нагрузку

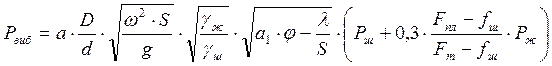
где а, а₁ – кинематические коэффициенты станка-качалки; D – внутренний диаметр труб; d – внутренний диаметр скважинного насоса.

Окончательно максимальная нагрузка в точке подвеса мо­жет быть определена по формуле

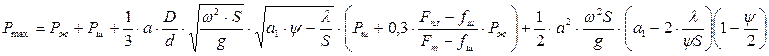Волна напряжений в колонне штанг будет распространяться снизу вверх. Достигнув точки подвеса, она увеличит нагрузку, после чего, отразившись пойдет вниз, отразится и пойдет вверх и т. д. В процессе распространения волн их энергия будет рас­сеиваться, и дополнительное усилие, обусловленное ими, при подходе к точке подвеса штанг будет все время убывать. Аналогичный процесс будет происходить при ходе штанг вниз в период упругих деформаций колонны штанг при переносе веса столба жидкости с штанг на трубы,

В результате колебательных процессов в колонне штанг на динамограмму усилий в точке подвеса штанг будут наложены две кривые, характеризующие процесс затухания колебаний, начинающихся в районе точек В^///и D^///.

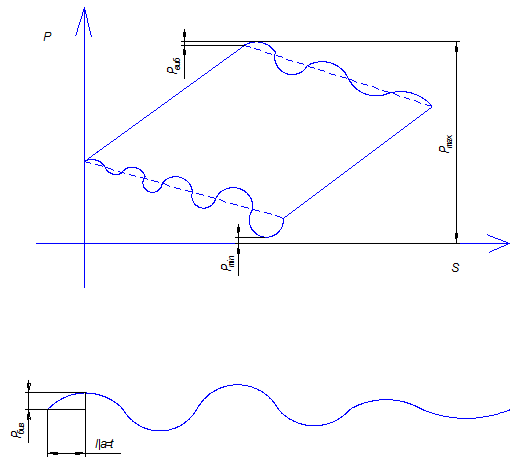
Рисунок 10.31, г – Динамограмма работы ШСНУ с учетом упругих

деформаций штанг и труб, инерционных

и вибрационных нагрузок

Для расчетов усилий, действующих в колонне штанг, а также в элементах привода имеют значения прежде всего максималь­ное и минимальное усилия, действующие в течение двойного хода штанг, поэтому математическое описание усилий мы огра­ничим приведенной выше формулой А.С. Вирновского.

В результате опытной проверки формул для определения максимального и минимального усилий А. Н. Адониным было установлено, что они с достаточной степенью точности позво­ляют определить эти усилия, и в настоящее время их исполь­зуют как эталонные при проверке результатов, получаемых с помощью других формул.

Вместе с тем эти формулы достаточно сложны, и многие исследователи предлагали более простые зависимости. А. Н. Адониным на основе большого количества экспериментальных данных были предложены следующие эмпирические зависи­мости с учетом критерий подобия.

(Р_ин + Р_деф) оказывают существенное влияние на работу штанговой колонны. При значительном их росте, как было доказано А. Н. Адониным, штанговая колонна достигнет резонанса.

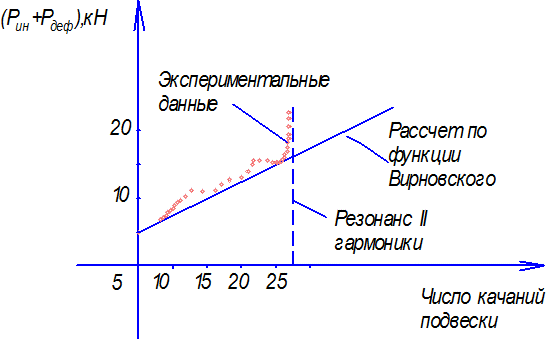
Рисунок 10.33 – Влияние на работу ШСНУ вибрационных

и инерционных составляющих усилий

в зависимости от числа качаний

Значительный рост динамической составляющей нагрузки ТПШ для скважин с заданным режимом отбора пластовой жидкости ставит предел применимости формулы А.С. Вирновского. Этот предел должен зависеть от двух параметров подобия насосной установки:

1) динамического подобия

μ = ω∙L/a (параметр Коши);

2) геометрического подобия S₀/L.

Оба этих параметра характеризуют интенсивность вынужденных упругих колебаний штанговой колонны. Вследствие несовершенства кинематики станка-качалки в колонне возникают вынужденные колебания двойной (по отношению к числу качаний) частоты. Совпадение частоты собственных колебаний с этой двойной частотой (резонанс второй гармоники) вызывает резкое возрастание динамических усилий в штангах. Резонанс второй гармоники начинается при μ = 0,785, но рост усилий начинается при меньших значениях μ.

Работу штанговой скважинной насосной установки А.Н. Адонин предложил разделить на два режима: статический и динамический, и для каждого режима была предложена своя упрощенная формула А.С. Вирновского. Различать режимы он предложил по параметру Коши – отношению частоты вынужденных колебаний штанги к частоте собственных.

Для статического режима работы установки μ = ω∙L/a ≤ 0,35, где а — скорость звука в металле, ω – угловая скорость кривошипа, L – длина колонны

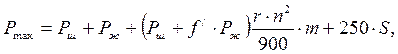
где , ,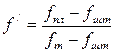

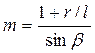β – значение угла φ в момент начала хода штанг вверх;

для динамического режима при μ > 0,35

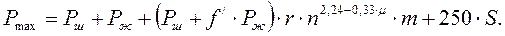
Приведенные формулы позволяют с меньшей точностью, но зато проще и быстрее вычислять Р_max при работе насосной установки.

В очень глубоких скважинах при длине ходе 4-6 м и небольших силах трения требуется ограничение и по геометрическому параметру.

Помимо определения усилий, действующих в точке подвеса штанг, представляет интерес определение длины хода плунжера относительно цилиндра скважинного насоса с учетом упругих деформаций штанг и труб.

Когда точка подвеса штанг движется по гармоническому закону, длина хода плунжера определяется по формуле

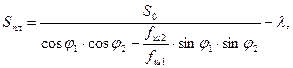
где φ_1,2 = ω∙1_1,2/а;

1₁, 1₂ – длина ступеней колонны с площадью штанг соответственно f_ш1, f_ш2;

λ – упругие деформации от статической нагрузки.

Следует отметить, что в рассмотренных формулах нагрузка от веса столба жидкости над плунжером скважинного насоса определялась исходя из того, что уровень пластовой жидкости находится у приема насоса, а противодавление на устье отсут­ствует.

Заключение

Рассмотренные вопросы динамики станка-качалки оказывают существенное влияние на работу всей ШСНУ. Проектирование четырехзвенника и выбор режима эксплуатации скважин с помощью ШСНУ требует ограничение динамическими условиями работы. Отсутствие или незначительная их составляющая способствует нормальной продолжительной работе ШСНУ.

Список использованных источников

1. Молчанов Г.В., Молчанов А.Г. Машины и оборудование для добычи нефти и газа. Учебник для вузов. – М.: Недра, 1984. – 464 с.

2. Чичеров Л.Н. Нефтепромысловые машины и механизмы. - М., Недра, 1983. – 308 с.

Лекция 10.7

Введение

Станок-качалка работает при циклической переменной нагрузке на головке балансира. Работа привода станка-качалки неравно­мерна в пределах одного цикла, т. е. хода штанг вверх и вниз.

Если станок-качалка не уравновешен, то при ходе вверх ее двигатель поднимает колонну штанг и преодолевает давление жидкости на плунжер насоса. В эту часть цикла он полностью загружен. При ходе вниз штанги опускаются под действием собственного веса. Нагнетательный клапан в плунжере открыт, и давление жидкости на штанги не действует. В этот период штанги раскручивают двигатель.

Таким образом, первая задача– уравновешивание станка-качалки и расчет параметров уравновешивания, т. е. усилий или сил тяжести грузов и места их размещения.

Но нагрузка при уравновешивании привода станка-качалки хотя и становится положительной при ходе штанг вниз, но пере­менна в пределах одного хода штанг вверх и вниз. Поэтому необ­ходимо определить наиболее рациональную мощность привода. Основным параметром, определяющим мощность, является тангенциальное усилие на пальце кривошипа станка-качалки (рисунок 10.34, а). Оно и радиус вращения пальца кривошипа определяют крутящий момент, а совместно с угловой скоростью вращения – и мощность двигателя. Следовательно, вторая задача – определение тангенциального усилия на пальце кривошипа.

Решение этих задач позволит перейти к определению мощности приводастанка-качалки, затем усилий, действующих на отдельные узлы, и к прочностным расчетам узлов и деталей.

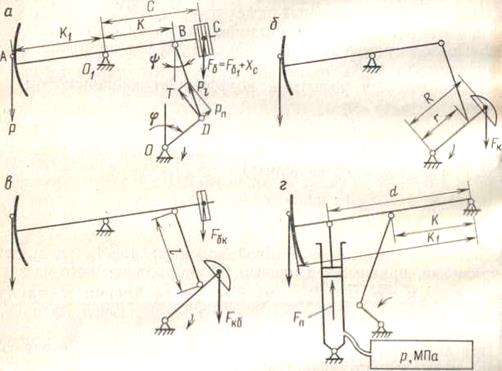
Рисунок 10.34 – Схемы станков-качалок с различными методами

уравновешивания

Основная часть

Методы уравновешивания станков-качалок

Уравновешиванием станков-качалок добиваются более равномерной нагрузки двигателя. Методы уравновешивания балансирных станков-качалокделятся на механические(с помощью противовесов) и пневматические (с помощью давления газа или воздуха). При первом методе уравновешивания грузы могут быть разме­шаны на балансире, на кривошипе или на обеих этих деталях. Со­ответственно и уравновешивание называется балансирным, криво­шипным или комбинированным (рисунок 10.34, а-в). Балансирное уравновешиванию применяют настанках-качалках меньшей грузо­подъемности (20-30 кН). При увеличении грузоподъемности груз на балансире становится очень большим – и при возвратно-поступательном движении возникают значительные инерционные силы.Эти силы отрицательно влияют па работоспособность узлов и соединений станка-качалки.При кривошипном уравновешивании груз, расположенныйна кривошипе, совершает равномерное вра­щение. При этом возникает лишь инерционная сила, направленная по радиусу вращения. Она воспринимается подшипниками криво­шипного вала и не влияет на работоспособность других узлов станка-качалки. Поэтому в мощных станках-качалках (80-200 кН) при­меняют только кривошипное уравновешивание.В установках средней мощности (40-60кН) применяютпереходное, комбинированное уравновешивание.

Кроме грузового уравновешиванияможет применяться и пневматическое (рисунок 10.34, г), при котором давление сжатого газа или воздуха действует на поршень, соединенный штоком с передним плечом балансира. Таким образом, сила давления компенсирует влияние части веса груза, действующего вточке подвеса штанг. Этот метод не требует больших дополнительных грузов, а следовательно, не возникает значительных инерционных усилий, вредных для узлов станка-качалки.

Уравновешивающие грузы или усилия рассчитываютпринципиально различными способами, в основу которыхположено:

1) равенство работ привода приходе штангвверх и вниз;

2) сведения кминимуму суммы квадратов отклонений тангенциального усилия напальце кривошипаот его среднего значения.

Первый способ наиболее простой,но менее точный. Он базируется на элементарной теорииработы установки штангового насоса.

Второй способ сложнее, но точнее. Он базируется на условии работы установок, приближающихся к реальным. В то же время анализ первого и второго способов показывает, что в условиях работы современных станков-качалок различие в результатах расчетов по первому и второму способам не столь велико.

Далее приведен первый способ расчета, а по второму даны лишь исходные данные и результирующие зависимости. В качестве примера описан метод балансирного уравновешивания.

Выражение для работы, выполняемой станком-качалкой при ходе вверх и вниз на основе элементарной теории, имеет вид:

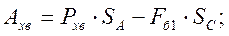
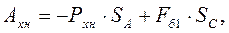
где Р_хв=Р_шв+ΔР_ж; Р_хн= Р_шж;

F_б1 – сила тяжести уравновешивающего груза, не учитывающего неуравновешенность узла станка-качалки;

S_С – перемещение (путь) груза.

Силами трения пренебрегают. Инерционные силы в первой и во второй половинах хода вверх имеют разные знаки, поэтов сумму их работ можно приравнять к нулю (аналогично при ходе вниз).

Приравнивая работы при ходе вверх и вниз, находим:

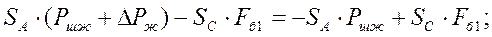
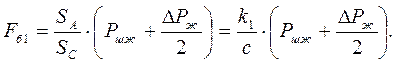
Значения k₁ и с – показаны на рисунке 10.34.

Таким образом, вес противовеса должен быть равен сумме веса колонны штанг и половины усилия от давления жидкости на плунжер. Причем при ходе штанг вверх двигатель будет преодолевать половину усилия от давления жидкости на плунжер, а при ходе штанг вниз – вес части противовеса, соответствующий по величине того же усилия.

Поскольку станок-качалка может быть неуравновешенной системой, следует определить вес груза, его уравновешивающего. Эту величину можно найти из суммы моментов весов отдельных частей станка-качалки относительно опоры балансира: