Основные операции над элементами списка
Рассмотрим более подробно, как выполняются основные операции с линейными односвязными списками.
Исходные установки. В начале программы необходимо описать элемент и его тип:
Type tpel =^element; {тип «указатель на элемент»}
element=record
пит; integer; {число}
p:tpel; {указатель на следующий элемент}
end;
В статической памяти описываем переменную - указатель списка и несколько переменных - указателей, используемых при выполнении операций со списком:
Var first, {указатель списка - адрес первого элемента списка}
n, f,q:tpel; {вспомогательные указатели}
Исходное состояние «список пуст»:
first: = nil;
Добавление нового элемента к списку. Добавление элемента к списку включает запрос памяти для размещения элемента и заполнение его информационной части. Построенный таким образом элемент добавляется к уже существующей части списка.
В общем случае при добавлении элемента к списку возможны следующие варианты:
§ список пyст, добавляемый элемент станет единственным элементом списка;
§ элемент необходимо вставить перед первым элементом списка;
§ элемент необходимо вставить перед заданным (не первым) элементом списка;
§ элемент необходимо дописать в конец списка.
Добавление элемента к пустому списку состоит из записи адреса элемента в указатель списка, причем в поле «адрес следующего» добавляемого элемента необходимо поместить nil:
new(first); {запрашиваем память под элемент}
first^.num:=5; {заносим число в информационное поле}
first^.р:=nil; {записываем nil в поле «адрес следующего»}
Добавление элемента перед первым элементом списка. При выполнении этой операции необходимо в поле «адрес следующего» переписать адрес первого элемента списка, а в указатель списка занести адрес добавляемого элемента:
new(q); {запрашиваем память под элемент}
q^.пит:=4; {заносим число в информационное ноле}
q^.p:=first; {в поле «адрес следующего» переписываем
адрес первого элемента}
first:=q; ... {в указатель списка заносим адрес нового элемента}
Добавление элемента перед заданным (не первым). Для выполнения операции необходимо знать адреса элементов, между которыми вставляется элемент, так как адресные части этих элементов при выполнении операции будут корректироваться. Пусть f- адрес предыдущего элемента, а n - адрес следующего элемента, тогда:
new(q); {запрашиваем память под элемент}
q^.num:=3; {заносим число в информационное поле}
q^.p:=n; {в поле «адрес следующего» нового элемента
переписываем адрес следующего элемента}
f^.p:=q; {в поле «адрес следующего» предыдущего
элемента заносим адрес нового элемента}
Минимально для вставки элемента в линейный одпосвязный список необходимо знать только адрес предыдущего элемента, так как тогда адрес следующего элемента известен – 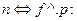
new(q); {запрашиваем память под элемент}
q^.num:=3, {заносим число в информационное поле}
q^.р:=f^.р; {в ноле «адрес следующего» нового элемента переписываем
адрес следующего элемента}
f^.p:=q; ... {в поле «адрес следующего» предыдущего элемента
заносим адрес нового элемента}
Добавление элемента в конец списка. В этом случае должен быть известен адрес элемета, после которого добавляется новый элемент:
new(q); {запрашиваем память под элемент}
q^.num:=7; {заносим число в информационное поле}
q^.p:=nil; {в поле «адрес следующего» элемента записываем nil}
f^.p:=q;... {в поле «адрес следующего» предыдущего элемента
заносим адрес нового элемента}
Анализ показывает, что этот случай можно свести к предыдущему, так как адресная часть последнего элемента содержит nil:
new(q); {запрашиваем памян» под элемент}
q^.num:=7; {заносим число в информационное поле)
q^.p:=f^.p; {в поле «адрес следующего» нового элемента
записываем nil}
f^.p:=q; ... {в поле «адрес следующего» предыдущего элемента
заносим адрес нового элемента}
Комбинируя эти фрагменты можно организовать построение списка с любой дисциплиной добавления элементов.
Пример. Разработагь программу, которая строит список по типу стека из целых чисел, вводимых с клавиатуры. Количество чисел не известно, но отлично от нуля. Конец ввода - по комбинации клавиш CTRL-Z (конец файла на устройстве ввода).
Обычно построение списка по типу стека выполняется в два этапа: в список заносится первый элемент, а затем организуется цикл добавления элементов перед первым:
ReadLn(a);
New(first); {запришиваем память под элемент}
first^.num=a; {заносим число в информационное поле}
first^.р:=nil; {записываем nil в поле «адрес следующего»}
white not EOF do
begin
ReadLn(a);
new(q); {запрашиваем память под элемент}
qA.num:=a; {заносим число в информационное поле}
q^.p:=first; {в поле «адрес следующего» переписываем
адрес первого элемента}
first:=q; {в указатель списки заносим адрес нового элемента}
end; ...
Пример. Разработать программу, которая строит список по типу очереди из целых чисел, вводимых с клавиатуры. Количество чисел не известно, но отлично от пуля. Конец вводя - по комбинации CTRL-Z (конец файла на устройстве ввода).
При построении списка по типу очереди сначала мы заносим в стек первый элемент, а затем организуем цикл добавления элементов после последнего, приняв во внимание, что nil необходимо разместить в адресном поле только последнего элемента:
Remlln(a);
new (first); {запрашиваем память под элемент}
first^.пит:=а; {заносим число в информационное пале}
f:=ftrst; {f - текущий элемент, после которого
добавляется следующий}
while not EOF do
begin
ReadLn(a);
new(q); {запрашиваем память под элемент)
q^.num:=a; {заносим число в информационное поле}
f^.p:=q; {в поле «адрес следующего» предыдущего
элемента заносим адрес нового элемента}
f:=f^.p; {теперь новый элемент стал последним}
end;
q^.p:=nil; {в поле «адрес следующего» последнего
элемента записываем nil}
Этот фрагмент можно упростить, если заметить, что новый элемент к списку можно добавлять сразу при запросе памяти:
ReadLn(a);
new(first); {запрашиваем памшь под элемент}
first^.пит:=а; {заносим число в информационное поле}
f:=ftrst; {f - текущий элемент, после которого
добавляется следующий}
while not EOF do
begin
ReadLn(a);
new(f^.p); {запрашиваем память под элемент}
f:=f^.р; {теперь новый элемент стал последним}
f^.num:=a; {заносим число к информационное иоле}
end;
f^.р:=пil;... {в поле «адрес следующего» последнего
элемента записываем nil}
Пример. Разработать программу, которая строит список, сортированный по возрастанию элементов, из целых чисел, вводимых с клавиатуры. Количество чисел не известно, но отлично от нуля. Конец ввода - по комбинации CTRL -Z (конец файла на устройстве ввода).
Список сортирован, соответственно, добавляя элемент, необходимо сохранить закон сортировки: элемент должен вставляться перед первым элементам, который больше, чем добавляемый. В зависимости от конкретных данных он может вставляться в начало, середину и конец списка.
new(first); {запрашиваем память под первый элемент}
ReadLn(first^.num); {заносим число в информационное поле}
first^.p:=nil;
while not EOF do
begin
new(q); {создаем элемент}
ReadLn(q^.num); {заносим значение}
If q^.num<first^.num then {если элемент меньше первого элемента
списка, то}
begin {вставляем перед первым}
q^.p:=ftrst;
first:=q;
end
else {иначе, вставляем в середину или конец}
begin
n:=first;{указатель на текущий элемент}
f:=first; {указатель на предыдущий элемент}
flag:= false; {"элемент не вставлен"}
{цикл поиска места вставки}
while (n^.p<>nil) and (not flag) do
begin
п:=п^.р; {переходим к следующему элементу}
if q^.num<n^.num then {место найдено}
begin {вставляем в есредину}
q^.p:=f^.p;
f^.p:=q;
flag:=true; {"элемент вставлен"}
end
else
f:=n; {сохраняем адрес текущего элемента}
end;
if not flag then {если элемент не вставлен, то}
begin {вставляем после последнего}
q^.p:=nil;
f^.p:=q;
end;
end;
end;
Просмотр и обработка элементов списка.Просмотр и обработка элементов списка выполняется последовательно с использованием дополнительного указателя:
f:=first;
while f<>nil da
begin
<обработка элемента по адресу f>
f:=f^.p;
end; …
В качестве примера рассмотрим вывод на экран элементов списка:
f:=first;
while f<>nil do
begin
WriteLn(f^.num,' ');
f:=f^.р;
end; …
Поиск элемента в списке. Поиск элементов в списке также выполняется последовательно, но при этом, как это и положено в поисковом цикле, обычно организуют выход из цикла, если нужный элемент найден, и осуществляют проверку после цикла, был ли найден элемент:
F:=first;
flag:=false;
while (f<>nil) and (not flag) do
begin
if f^.пит=k then flag:=not flag
else f:=f^.p;
end;
if flag then <элемент найден>
else < элемент не найден>; ...
Удаление элемента из списка. При выполнении операции удаления также возможно четыре случая:
§ удаление единственного элемента;
§ удаление первого (не единственного) элемента списка;
§ удаление элемента, следующего за данным;
§ удаление последнего элемента.
Удаление единственного элемента. После удаления единственного элемента список становится пустым, следовательно при выполнении этой операции необходимо не только освободить память, выделенную для размещения элемента, но и занести nil в укачатель списка first:
Dispose(first);
First:=nil; ...
Удаление первого (не единственного) элемента списка. Удаление первого элемента состоит из сохранения адреса следутощего элемента в рабочей неременной f, освобождения памяти элемента и записи в указатель списка сохраненного адреса следующего элемента:
f:=first^.p; {сохраняем адрес следующего элемента}
Dispose (first); {освобождаем память}
first:=f; ... {заносим в указатели списка адрес следующего элемента}
Удаление единственного элемента и перкого элемента в программе можно объединить:
q: =first;
first: =ftrst^.p;
Dispose(q);...
Удаление элемента, следующего за данным (не последнего). Удаление элемента, следующего за данным, требует запоминания адреса удаляемо элемента, изменения адресной части данного элемента и освобождения и памяти.
n:=f^.р; {сохраняем адрес удаляемого элемента}
f^.р:=п^.р; {заносим в адресное поле предыдущего элемента адрее следующего элемента}
Dispose(n); .. {освобождаем память}
Удаление последнего элемента. Удаление последнего элемента отличается только тем, что в поле «адрес следующего» заданного элемента записывается константа nil:
n:=f^.р;
f^.р:=пil;
Dispose(n); ...
Удаление последнего элемента можно свести к удалению элемента, следующего за данным, так как адресная часть удаляемою элемента равна nil.
Комбинируя приемы удаления, мы также можем организовать любую дисциплину удаления.
Пример. Разработать программу, которая удаляет из списка все элементы меньше заданного значения k.
Удаляемые значения могут располагаться в списке на любом месте, следовательно, возможны все четыре варианта удаления элемента, котрые сводятся к двум случаям:
§ удаление единственного элемента и удаление записей из начала списка – удаление из начала списка;
§ удаление средних и последнего элементов - удаление не из начала списка.
Для разделения этих двух случаев введем специальный признак «удаление из начала», который в начале установим равным true, а затем, как только в списке будет оставлен хотя бы один элемент - изменим на false.
n:=first;
nft:=true; {признак «удаление из начала списка»}
repeat
if п^.пит<к then
begin
if nft then {если «удаление из начала списка»}
begin {удаление из начала списка}
q:=first;
first:=first^.p;
Dispose (q);
n:=first; {переходим к следующему элемету}
end
else {иначе}
begin {удаление из середины и конца}
q:=n;
п:=п^.р; {переходим к следующему элементу}
Dispose(q);
f.р:=п;
end
end
else {оставляем элемент в списке}
begin
f:=n; {устанавливаем адрес предыдущего элемента}
n:=n^.p; {переходим к следующему элемент))
nft:=not nft; {«удаление не из начала списка»}
end;
until n=nil;... {до завершения списка}
Лекция 24. Сортировка массивов(2 часа)
Сортировка - это процесс упорядочивания информации по определенному признаку. Цель сортировки - облегчение последующего поиска элементов. Это почти универсальный вид обработки информации, с которым мы встречаемся в жизни повсеместно.
Существует огромное количество методов сортировки и, соответственно, алгоритмов их реализации. Часть из этих алгоритмов в некотором смысле оптимальна, другие имеют свои достоинства и недостатки. Поэтому, прежде чем использовать алгоритм, реализующий какой-либо метод, следует выполнить анализ его производительности в конкретных условиях.
В качестве оценки производительности методов обычно используют функциональную зависимость времени работы программы от размерности исходного массива t(n). При анализе алгоритмов в первую очередь интерес представляет характер зависимости при достаточно больших значениях размерности задачи (n→∞).
В математике характер зависимости часто определяют ее порядком. Порядком некоторой функции g(n) при достаточно больших n называют другую функцию g(n), такую что
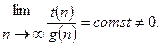
Это обозначается как t(n) = O[g(n)]
Например, для полинома f(n)=2n4-3n3+5n-6, порядком является полином n4, или f(n) = О(n4), так как
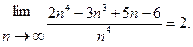
В программировании порядок зависимости времени работы программы, реализующей некоторый метод, от размерности исходных данных n называют вычислительной сложностью данного метода. Так, вычислительная сложность O(const) означает, что время решения задачи с использованием данного метода не зависит от размерности задачи, O(n) - время работы пропорционально размерности задачи. O(n2) - время работы пропорционально квадрату размерности задачи и т. д.
Примечание. Внекоторых случаях целесообразно различать, вычислительную сложность метода и его конкретной реализации, так как неудачная реализация может существенно ухудшить предпологаемую вычислительную сложность метода.
Временную сложность можно оценить, используя в качестве единиц измерения временные единицы (мкс, с и т. д.), а можно используя время выполнения основных, характеризующих процесс операции, количество которых соответствует количеству итераций (повторений) цикла, например, операций сравнения, операций пересылки. Время выполнения этих операций можно считать постоянным. Следовательно, функциональная зависимость количества выполняемых операций от размерности задачи по характеру будет совпадать с временной зависимостью.
На практике интересны методы сортировки, которые позволяют экономно использовать оперативную память, поэтому целесообразно рассмотрев только методы, не требующие использования дополнительных массивов. Такие методы в практике программирования называют прямыми. Самыми простыми из прямых методов являются:
§ метод выбора;
§ метод вставки;
§ метод обменов (метод пузырька).
Рассмотрим эти методы на конкретном примере.
Пример. Разработать программу сортировки элементов массива А(n), где n < 20, используя метод выбора, метод вставки и метод обменов. Оценить эффективность применения указанных методов.
Метод выбора. Сортировка посредством выбора представляет собой один из самых простых методов сортировки. Он предполагает такую последовательность действий:
Сначала находим минимальный элемент массива. Найденный элемент меняем местами с первым элемештум. Затем повторяем процесс с n-1 элемен-
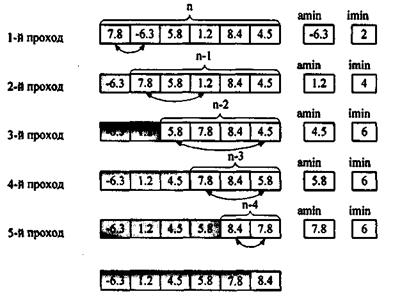
Рис. 1. Сортировка выбором
тами, начиная со второго, потом с n-2 элементами, начиная с третьего и т.д. до тех пор, пока не останется один, самый большой элемент массива (рис. 1).
Алгоритм сортировки выбором приведен на рис. 2. Ниже приведен текст программы, реализующий данный алгоритм.
 Program sort;
Program sort;
Var a:array[l.. 20] of real;
j, i, n, imin:integer;
min:real;Begin
Writeln('Введите количество чисел n<=20: ');
Readln(n);
Writeln('Введиme массив:');
for i:=1 to n do Read(a[i]);
Readln;
for j:=1 to n-1 do {цикл поиска минимальных
элементов массива}
begin
min:=a[j]; {начальное значение для
поиска минимума}
imin:=j; {начальное значение
индекса минимального элемента}
for i:=j+l to n do {цикл поиска минимума
и его индекса}
if a[i]<min then {если элемент меньше
уже найденного минимального}
Рис. 2. Алгоритм сортировки
выбором
Begin
min:=a[i]; {запоминаем элемент}
imin:=i {запоминаем его индекс}
end; {меняем местами найденный минимум и первый
элемент текущего массива}
a[imin]:=a[j];
a[j]:=min;
end;
for i:=l to n do Write(a[i]:6:2);
Writeln;
End.

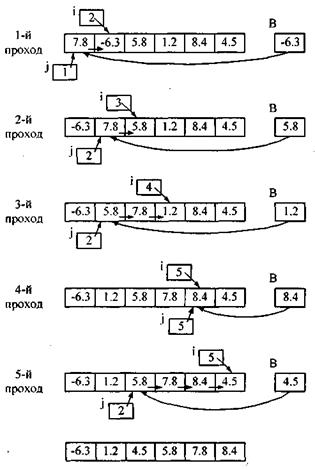
Рис. 3. Сортировка вставками Рис.4. Алгоритм сортировки
всавками
Оценим временную сложность данного метода, используя в качестве основной операции операцию сравнения.
Для поиска минимального элемента в каждом проходе потребуется выполнить: n-1, n-2, 1 операций сравнения, т.е. всего n(n-1)/2 операций сравнения. Следовательно, вычислительная сложность данного метода 0(n2). Причем время сортировки не зависит от исходного порядка элементов.
Метод вставки. Сортировку вставками можно описать следующим образом. В исходном состоянии считают, что сортируемая последовательность состоит из двух последовательностей: уже сортированной (она на первом шаге состоит из единственного - первого элемента) и последовательности элементов, которые еще необходимо сортировать. На каждом шаге из сортируемой последовательности извлекается элемент и вставляется в первую последовательность так, чтобы она оставалась сортированной. Поиск места вставки осуществляют с конца, сравнивая вставляемый элемент ai с очередным элементом сортированной последовательности а:. Если элемент аi больше аj, его вставляют вместо aj+1, иначе сдвигают а: вправо и уменьшают на единицу. Поиск места вставки завершают, если элемент вставлен или достигнут левый конец массива. В последнем случае элемент аi вставляют на первое место (рис. 3).
Разрабатывая алгоритм, избавимся от проверки достижения начала массива. Прием, позволяющий отменить эту проверку, называется «установкой барьера». С использованием этого приема проверка организуется так, чтобы из цикла поиска места вставки в любом случае происходил выход по первому условию. Для этого достаточно поместить вставляемый элемент перед первым элементом массива, как элемент с индексом 0. Этот элемент и станет естественным барьером для ограничения выхода за левую границу массива. Алгоритм сортировки вставками приведен на рис. 4. Ниже приведен текст программы, реализующей данный алгоритм.
Program sort2;
Var a:array[0..20]of real;
b:real;
i,j,n:integer;
Begin
WriteLn('Введите количество чисел n<=20.');
ReadLn(n);
WriteLn('Введите массив.');
for i:=1 to n do Read(a[i]); ReadLn;
for i:=2 to n do {начиная со второго элемента до конца массива}
begin
B:=a[i]; {запоминаем i-й элемент}
а[0]:=В; {этот же элемент записываем в а[0] - это барьер}
j:=i-l; {индекс i запоминаем в j}
while B<a[j] do {пока очередной рассматриваемый элемент
больше i-ro элемента}
begin
a[j+1]:=a[j]; {сдвигаем элемент}
j:=j-1; {уменьшаем j на 1}
end;
a[j+1]:=B; {как только найдено место, туда записывается В}
end;
WriteLn('Отсортированный массив:');
for i:=l to n do Write(a[i]:6:2);
WriteLn;
End.
Оценим временную сложность данного метода, также определив количество операций сравнения.
Для поиска места i-ro элемента каждый раз потребуется выполнить от 1 до i-1 операций сравнения, т.е. в среднем i/2 операций сравнения. Значение i изменяется от 2 до n, т.е. выполняется n-1 проход, в каждом из которых происходит в среднем от 1 до n/2 сравнений. Таким образом, суммарно в среднем для решения задачи требуется выполнить (n-1)(n/2 + 1)/2 = (n2 + n - 2)/4 операций сравнения. Откуда вычислительная сложность метода в среднем также равна Оср(n2), хотя время выполнения примерно в два раза меньше, чем у предыдущего метода. Интересно, что в данном случае вычислительная сложность зависит от исходного расположения элементов массива.
Так, в лучшем случае, когда массив уже упорядочен, поиск места вставки требует одного сравнения для каждого элемента, и количество сравнений равно n-1. Соответственно, вычислительная сложность равна Ол(n).
В худшем случае, если элементы массива в исходном состоянии расположены в обратном порядке, поиск места вставки для каждого элемента потребует: 1, 2, 3, ..., n-1 сравнения, следовательно, всего потребуется n(n-1)/2 операций сравнения, т. е. время выполнения программы примерно совпадет со временем программы, реализующей метод выбора. Значит вычислительная сложность в худшем, так же как в среднем, равна Ох(n2).
Таким образом, за счет ускорения сортировки в лучших случаях данный метод имеет лучшие временные характеристики, чем предыдущий.
Метод обменов. Алгоритм прямого обмена основывается на сравнении пары соседних элементов. Если расположение элементов не удовлетворяет условиям сортировки, то их меняют местами. Сравнения и перестановки продолжают до тех пор, пока не будут упорядочены все элементы. Определить, что элементы упорядочены, можно, считая количество выполненных перестановок: если количество перестановок равно нулю, то массив отсортирован (рис. 5).
Простейший алгоритм сортировки с помощью обмена представлен на рис. 6. Ниже приведена программа, реализующая данный алгоритм.
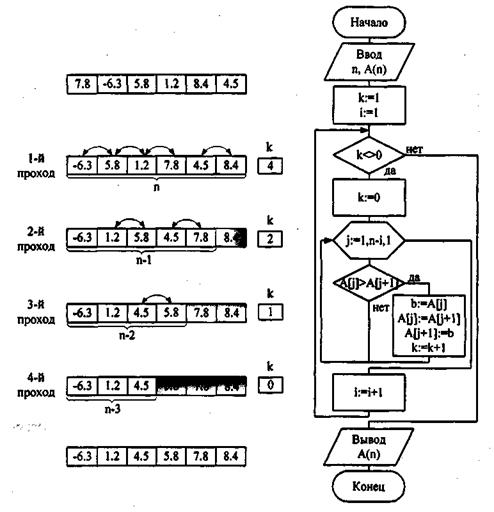
Рис. 5. Сортировка обменом Рис.6. Алгоритм сортировки
обменом
Program ex;
Var a: array[1..20] of Real;
i,j,n,l,k: integer;
b:real;
Begin
WriteLn('Введите размер массива N< =20');
ReadLn(n);
for i := 1 to n do Read(a[i]);
ReadLn;
WriteLn('Исходный массив:');
for i := 1 to n do Write(a[i]:7:2);
WriteLn;
k:=1; {количество перестановок, начальное значение не равно 0 }
i:=1; {номер очередного просмотра, в начале равен 1}
while k<>O do {пока есть перестановки}
begin
к:=0; {обнуляем количество перестановок}
for j:=1 to n-i do {цикл сравнения соседних элементов}
If a[j]>a[j+1] then {если предыдущий элемент больше, то}
begin {осуществляем перестановку}
b:=a[j];
a[j]:=a[j+1]; a[j+1]:=b;
к:=к+1; {счетчик перестановок увеличиваем на 1}
end;
i:=i+l; {увеличиваем номер просмотра на 1}
end;
WriteLn('Отсортированный массив ');
for i := 1 to n do Write(a[i]:7:2);
WriteLn;
WriteLn(' Количество проходов ', i:3);
End.
Оценим вычислительную сложность данного метода. Очевидно, что она сильно зависит от исходного расположения элементов массива. Так, в лучшем случае, если массив был уже отсортирован, потребуется выполнить n-1 сравнение для проверки правильности расположения элементов массива, т. е. вычислительная сложность в лучшем Ол(n).
В худшем случае, если массив отсортирован в обратном порядке, будет выполнено n-1, n-2, ...1 операций сравнения, т. е. всего (n2-n)/2 операций сравнения, следовательно, вычислительная сложность в худшем определяется как Ох(n2).
Выполнить усредненную оценку данного метода достаточно сложно, так как в отличие от предыдущих случаев зависимость времени выполнения от количества неправильно стоящих элементов не является линейной. Например, два элемента, стоящие на своем месте в начале массива, практически не повлияют на время сортировки, а два элемента, стоящих на своем месте в конце массива, вызовут ее досрочное завершение. По результатам тестирования можно считать, что в среднем этот метод сортировки обесценивает время примерно в два раза лучше, чем предыдущий. Вычислительная сложность в среднем данного метода Оср(n2).
Примечание. По материалам данною раздела можно сделать ошибочный вывод, что всеметоды сортировки в среднем имеют вычислительную сложность О(n2). Методы сортировки, рассмотренные в данном разделе, не являются самыми быстрыми, они просто самые простые и потому используются чаще всего. Существуют методы быстрой сортировки, которыс обеспечивают в среднем и даже в худшем вычислительную сложность О(n log2 n). Разработаны также методы, обеспечивающие для специальных данных вычислительную сложность Оср(n).
Лекция №25 (2 часа)
Директивы компилятора
Дата добавления: 2015-12-01; просмотров: 1455;
