Основні способи класифікації
| Спосіб спектрального кута | Спосіб мінімальної відстані | Спосіб паралелепіпедів | |
| Спосіб спектрального кута дає гарні результати, коли потрібно провести класифікацію для об’єктів, які мають схожі значення яскравості | Спосіб мінімальної відстані використовують, коли області значення яскравості об’єктів пересікаються. | Спосіб паралелепіпедів застосовують, коли області значення яскравості об’єктів не пересікаються | |
| Спосіб максимальної правдоподібності | Спосіб дистанції Махаланобіса | Бінарне кодування | |
| Цей спосіб застосовують в особливо складних випадках, коли області значень яскравості різних класів у просторі ознак перекриваються і мають складну (або витягнуту) форму | Цей спосіб є більш точнішим, порівняно зі способом мінімальної відстані, оскільки враховує розподіл значень яскравості вибірок, що навчають | Цей спосіб застосовують, якщо всі пікселі на знімку потрібно розділити на два класи | |
Спосіб спектрального кутадає гарні результати, коли потрібно провести класифікацію для об’єктів, які мають схожі значення яскравості у всіх спектральних діапазонах. Крім того, оскільки цей спосіб не враховує значення яскравості пікселів, то на результати не впливають і ефекти засвічування знімків.
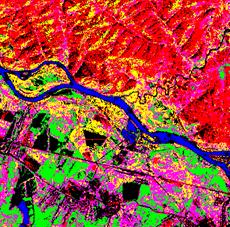
Приклад класифікації об’єктів за допомогою способу спектрального кута представлений на рис. 8.24.

| 
| 
|
| а) | б) | |
| Рис. 8.24. Приклад класифікації об’єктів за допомогою способу спектрального кута: а) первісний знімок зроблений за допомогою КА Landsat; б) результат класифікації способом спектрального кута |
При класифікації способом спектрального кута:
1) попередньо створюють еталонні ділянки;
2) всі пікселі знімка, в тому числі і еталонні, розглядаються як вектори в просторі спектральних ознак (рис. 8.25);
3) задається максимально допустимий спектральний кут, тобто, якщо кут між еталонним вектором і вектором пікселя, який зазнає класифікації менше максимального, то цей піксель відноситься до даному класу, якщо більше – не відноситься.
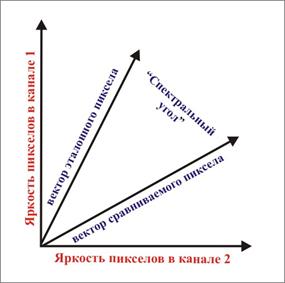
Рис. 8.25. Ілюстрація способукласифікації об’єктів за допомогою способу спектрального кута
Примітка. Класи, отримані способом спектрального кута, залежать від кута між векторами яскравості пікселів і не залежать від довжини вектора (значення яскравості).
Спосіб мінімальної відстанівикористовують, коли спектральні ознаки різних класів схожі, і діапазони значень їх яскравості перекриваються.
Приклад класифікації об’єктів за допомогою способу спектрального мінімальної відстані представлений на рис. 8.26.

| 
| 
|
| а) | б) | |
| Рис. 8.26. Приклад класифікації об’єктів за допомогою способу мінімальної відстані: а) первісний знімок зроблений за допомогою КА Landsat; б) результат класифікації способом мінімальної відстані |
У процесі класифікації способом мінімального спектральної відстані:
1) попередньо створюють еталонні ділянки;
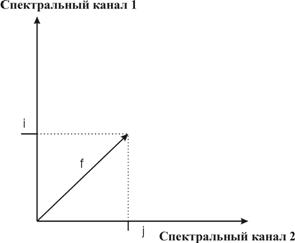
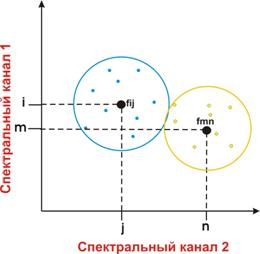
2) значення яскравості пікселів розглядаються як вектор fij в просторі спектральних ознак, i та j – це значення яскравості пікселя в різних спектральних каналах (рис. 8.27);
3) розраховується спектральна відстань між еталонними векторами і векторами значень яскравості всіх пікселів знімка, відстань між двома векторами (r) розраховується по формулі:

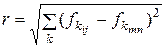 ,
,
де k – номер спектрального каналу; це відстань (як видно з формули) розраховується сукупно по всіх спектральних каналах;
4) далі відбувається розподіл пікселів по класах, якщо відстань від даного вектора до еталонного менше заданого значення (яке задають попередньо), то цей вектор відносять до даного класу, якщо відстань більше заданого значення, відносять в інший клас або взагалі не відносять у жодний з класів (рис. 8.28).
| 
|
| Рис. 8.27. Ілюстрація способукласифікації об’єктів за допомогою способу мінімальної відстані | Рис. 8.28. Графічнаілюстрація класифікації за способом мінімальної відстані |
У двовимірному просторі спектральних ознак одержані класи виглядають як округлі області, в багатовимірному просторі, як кулеподібні області.
Примітка. Недолік даного методу полягає в тому, що при його застосуванні не враховується розподіл (дисперсія) значення яскравості пікселів в еталонних ділянках.
Спосіб паралелепіпедів застосовують, коли області значення яскравості об’єктів не перетинаються. Приклад класифікації об’єктів за допомогою способу паралелепіпедів представлений на рис. 8.29.

| 
| 
|
| а) | б) | |
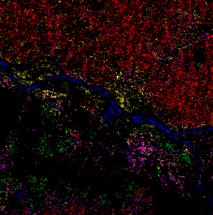
| Рис. 8.29. Приклад класифікації об’єктів за допомогою способу паралелепіпедів: а) первісний знімок зроблений за допомогою КА Landsat; б) результат класифікації способом паралелепіпедів |
У процесі класифікації способом паралелепіпедів:
– попередньо створюють еталонні ділянки;
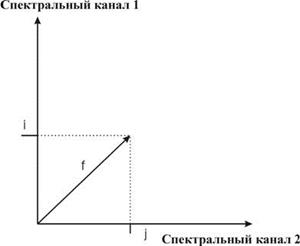
– значення яскравості пікселів розглядається як вектор fij в просторі спектральних ознак, i та j це значення яскравості пікселя в різних спектральних каналах (рис. 8.30);
| 
|
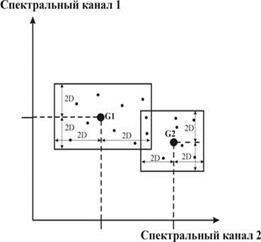
| Рис. 8.30. Ілюстрація способукласифікації об’єктів за допомогою способу паралелепіпедів | Рис. 8.31. Графічнаілюстрація класифікації способом паралелепіпедів |
– розраховується спектральна відстань між еталонними векторами і векторами значень яскравості всіх пікселів знімка,
– відстань між двома векторами (r) розраховується за формулою:
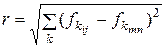 ,
,
де k – номер спектрального каналу.
Ця відстань (як видно із формули) розраховується сукупно по всіх спектральних каналах, тобто все як у способі мінімальної відстані, але спосіб паралелепіпедів використовує дисперсію (D) що робить цей метод більш точним, оскільки відомо, що для вибірки, значення якої розподілені у відповідності з нормальним законом, 95.5% її значень лежать в межах відхилень від середнього значення, менше чим 2D (рис. 8.31), тому, при класифікації методом паралелепіпедів у даний клас включаються пікселі, значення яскравості яких відстоять від середнього навчальної вибірки менше чим на 2D.
Якщо намалювати отримані області класів на площині (двовимірний простір ознак) то отри мана фігура буде прямокутником, в тривимірному просторі – паралелепіпедом.
Примітка. Прямокутники можуть частково перекриватись, що призводить до невизначеності.
Спосіб максимального правдоподібностірозраховує імовірність, з якою даний піксель належить до якогось класу. Кількість і параметри класів задаються користувачем, шляхом указівки навчальних вибірок. Кожен піксель відноситься до того класу, до якого він може належати з найбільшою імовірністю. При розрахунку імовірності враховується яскравість пікселя і яскравості пікселів, що його оточують.
У двовимірному просторі спектральної яскравості, отримані даним способом класи, описуються еліпсами, а в багатовимірному – еліпсоїдами (рис. 8.32).
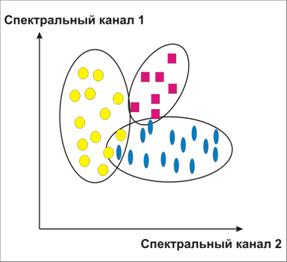
Рис. 8.32. Графічнаілюстрація класифікації способом максимальної правдоподібності
Приклад класифікації об’єктів за допомогою способу паралелепіпедів представлений на рис. 8.33.

| 
| 
|
| а) | б) | |
| Рис. 8.33. Приклад класифікації об’єктів за допомогою способу максимальної правдоподібності: а) первісний знімок зроблений за допомогою КА Landsat; б) результат класифікації способом максимальної правдоподібності |
Спосіб дистанції Махаланобіса.Цей спосіб класифікації схожий на спосіб мінімальної відстані, але відрізняється тим, що в процесі класифікації вимірюється не евклидова (як у способі мінімальної відстані), а відстань Махаланобіса. Це означає, що цей спосіб ураховує розподіл (дисперсію) значень яскравості пікселів в еталонних ділянках. Тому, якщо евклідова відстань від вектора яскравості даного пікселя, до двох еталонних векторів однакова, то цей піксель буде віднесений до того класу, дисперсія еталонної вибірки якого більше.
Приклад класифікації об’єктів за допомогою способу дистанції Махаланобіса представлений на рис. 8.34.

| 
| 
|
| а) | б) | |
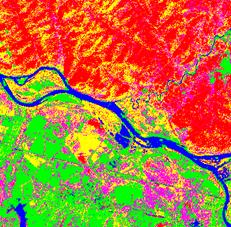
| Рис. 8.34. Приклад класифікації об’єктів за допомогою способу дистанції Махаланобіса: а) первісний знімок зроблений за допомогою КА Landsat; б) результат класифікації способом дистанції Махаланобіса |
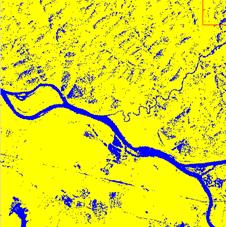
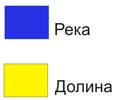
Бінарне кодування.Якщо на знімку всі пікселі потрібно розділити на два класи, наприклад, вода – суша, можна використати метод бінарного кодування. При бінарному кодуванні всім пікселям привласнюється одне з двох значень на основі порівняння зі значеннями еталонних вибірок. Під час класифікації значення кожного пікселя порівнюється із середнім еталонної вибірки. В результаті утворюється бінарне зображення.
Приклад класифікації об’єктів за допомогою бінарного кодування представлений на рис. 8.35.

| 
| 
|
| а) | б) | |
| Рис. 8.35. Приклад класифікації об’єктів за допомогою бінарного кодування: а) первісний знімок зроблений за допомогою КА Landsat; б) результат класифікації способом бінарного кодування |
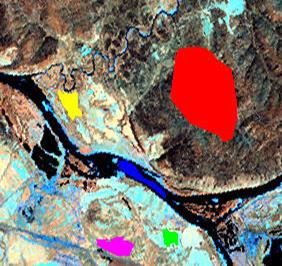
Вибір еталонних ділянок передбачає цифрування фрагментів знімку, однорідних за яскравістю і розташуванням (рис. 8.36).
| 
|
Рис. 8.36. Оцифровування еталонних ділянок
Згідно емпіричного правилу кожна еталонна ділянка повинна містити в 10-100 разів більше пікселів, чим кількість спектральних каналів знімка.
Способи оцінки якості еталонних ділянок:
а) побудувати і оцінити криву розподілу значень яскравості пікселів на обраній ділянці: характер розподілу повинен підкорятися нормальному (гаусовому) закону розподілу. Для оцінки однорідності навчальної вибірки, потрібно оцінити величину дисперсії, якщо дисперсія має високе значення, то вибірка неоднорідна і класифікація відбудеться з великою кількістю помилок (рис. 8.37).
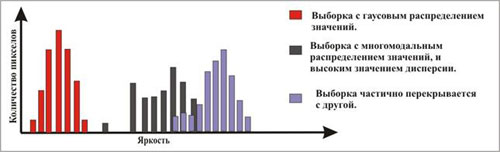
Рис. 8.37. Оцінка однорідності вибірки
б) Поєднати криві розподілу значень яскравості пікселів усіх навчальних вибірок, щоб оцінити їх розрізненість. Якщо вибірки значно перекриваються, то класифікація відбудеться з великою кількість помилок.
Після виконання процесу класифікації потрібно оцінити достовірність отриманих результатів. Оцінка достовірності здійснюється:
а) візуально, щоб виявити грубі помилки,
в) кількісно, тобто контрольні ділянки зображення, що класифікується порівнюють з наземними даними (картами, знімками крупного масштабу, літературними джерелами).
Якщо кількість помилок перевищує встановлені для конкретної задачі межі, то створюють нові навчальні вибірки, і процес класифікації повторюють.
Класифікація без навчанняце процес, при якому розподіл пікселів зображення відбувається автоматично, на основі аналізу статистичного розподілу яскравості пікселів.
Треба відзначити, що перед початком класифікації невідомо скільки, і яких об’єктів є на знімку, а після проведення класифікації необхідне дешифрування отриманих класів, щоб визначити, яким об’єктам вони відповідають.
Таким чином, класифікацію без навчання застосовують у випадку якщо:
а) заздалегідь невідомо які об’єкти є на знімку;
б) на знімку велика кількість об’єктів (болем 30) зі складними межами;
в) це попередній етап перед класифікацією з навчанням.
Найбільш поширеними методами класифікації без навчання є такі:
1. ISODATA;
2. K-Середніх.
ISODATA (Iterative Self-Organizing Data Analysis Technique) – ітераційна методика аналізу даних, що самоорганізується, яка заснована на кластерному аналізі. Основний параметр, що задається перед проведенням обчислень, – кількість кластерів, які необхідно отримати.
Приклад класифікації об’єктів за допомогою способу ISODATA представлений на рис. 8.38

| 
|
| а) | б) |
| Рис. 8.38. Приклад класифікації об’єктів за допомогою способу ISODATA: а) первісний знімок зроблений за допомогою КА Landsat; б) результат класифікації способом ISODATA |
Етапи класифікації ISODATA:
1) розрахунок статистичних параметрів розподілу яскравостей всього знімку в кожній спектральній зоні (мінімальне, максимальне, середнє значення, стандартне відхилення);
2) всі пікселі знімка поділяються на n рівних діапазонів у просторі спектральних ознак, для кожного з них визначається середнє значення і середнє відхилення;
3) перша ітерація кластеризації, тобто в просторі спектральних ознак для кожного пікселя розраховується спектральна відстань до середніх значень, і кожний піксель відносять до певного кластеру. В один кластер потраплять ті пікселі, між якими менше відстань у просторі спектральних ознак;
4) розрахунок реальних середніх значень для отриманих класів;
5) наступна ітерація з новими значеннями середніх, й уточнення границь класів, при цьому кількість класів може змінюватись.
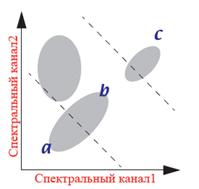
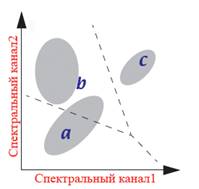
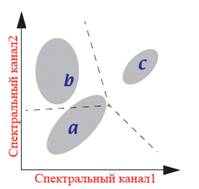
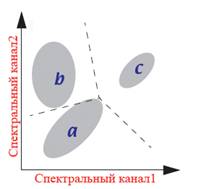
Процес триває до тих пір, поки не буде досягнута максимальна (заздалегідь встановлена) кількість ітерацій або досягнутий максимальний процент пікселів, що не змінили свій клас під час останньої ітерації (цей параметр також задається заздалегідь), рис. 8.39. Зазвичай цей параметр, так званий поріг збіжності, дорівнює 95-99 % усіх пікселів. Оскільки при певному розподілі значень яскравості на знімку такої стабілізації не відбувається, тому одночасно використовують другий обмежуючий параметр – максимальну кількість ітерацій.
| 
|
| 
|
| Рис. 8.39. Графічна інтерпретація класифікації способу ISODATA |
Спосіб ISODATA потребує значних обчислювальних ресурсів. Швидкість обробки залежить від заданої кількості класів, об’єму знімка, процесору, розміру оперативної памяті, програмного забезпечення. Проте за результатами обробки знімка за цим способом виявляється розподіл об’єктів з різними спектральними образами. Крім того спосіб ISODATA є параметричним, оскільки значення яскравості групуються навколо середнього значення яскравості кластера.
Метод класифікації без навчання K-Середніх відрізняється від методу ISODATA тим, що потребує початкового завдання певної кількості середніх значень для формування вихідних класів, отже, цей метод використовують, коли об’єкти на знімку добре розрізняються.
[1] Валідація – процес, що дозволяє визначити, наскільки точно з позицій потенційного користувача деяка модель представляє задані сутності реального світу.
Дата добавления: 2016-02-09; просмотров: 2862;
