Или же, в матричной форме,
RES = DCT T*IMG * DCT , (8.5)
где DCT – матрица базисных (косинусных) коэффициентов для преобразования размером 8×8, имеющая вид:

 .353553 .353553 .353553 .353553 .353553 .353553 .353553 .353553
.353553 .353553 .353553 .353553 .353553 .353553 .353553 .353553
.490393 .415818 .277992 .097887 -.097106 -.277329 -.415375 -.490246
.461978 .191618 -.190882 -.461673 -.462282 -.192353 .190145 .461366
DCT= .414818 -.097106 -.490246 -.278653 .276667 .490710 .099448 -.414486(8.6)
.353694 -.353131 -.354256 .352567 .354819 -.352001 -.355378 .351435
.277992 -.490246 .096324 .416700 -.414486 -.100228 .491013 -.274673
.191618 -.462282 .461366 -.189409 -.193822 .463187 -.460440 .187195
.097887 -.278653 .416700 -.490862 .489771 -.413593 .274008 -.092414
Итак, в результате применения к блоку изображения размером 8х8 пикселов дискретного косинусного преобразования получим двумерный спектр, также имеющий размер 8×8 отсчетов. Иными словами, 64 числа, представляющие отсчеты изображения, превратятся в 64 числа, представляющие отсчеты его DCT-спектра.
А теперь напомним, что такое спектр сигнала. Это – величины коэффициентов, с которыми соответствующие спектральные составляющие входят в сумму, которая в результате и дает этот сигнал. Отдельные спектральные составляющие, на которые раскладывается сигнал, часто называют базисными функциями. Для ПФ базисными функциями являются синусы и косинусы разных частот.
Для 8×8 DCT система базисных функций задается формулой
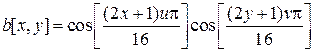 , (8.7)
, (8.7)
а сами базисные функции выглядят подобно приведенным на рис. 8.4.



Рис. 8.4. Вид базисных функций
Самая низкочастотная базисная функция, соответствующая индексам (0,0), изображена в левом верхнем углу рисунка, самая высокочастотная – в нижнем правом. Базисная функция для (0,1) представляет собой половину периода косинусоиды по одной координате и константу - по другой, базисная функция с индексами (1,0) – то же самое, но повернута на 90о. Дискретное косинусное преобразование вычисляется путем поэлементного перемножения и суммирования блоков изображения 8х8 пикселов с каждой из этих базисных функций. В результате, к примеру, компонента DCT-спектра с индексами (0,0) будет представлять собой просто сумму всех элементов блока изображения, то есть среднюю для блока яркость. В компоненту с индексом (0,1) усредняются с одинаковыми весами все горизонтальные детали изображения, а по вертикали наибольший вес присваивается элементам верхней части изображения и т.д. Можно заметить, что чем ниже и правее в матрице DCT его компонента, тем более высокочастотным деталям изображения она соответствует. Для того, чтобы получить исходное изображение по его DCT-спектру (выполнить обратное преобразование), нужно теперь базисную функцию с индексами (0,0) умножить на спектральную компоненту с координатами (0,0), прибавить к результату произведение базисной функции (1,0) на спектральную компоненту (1,0) и т.д.
В приведенной ниже табл. 8.7 видны числовые значения одного из блоков изображения и его DCT-спектра:
Таблица 2.9
Числовые значения блока изображения
| Исходные данные | |||||||
| Результат DCT | |||||||
| 235,6 | -1 | -12,1 | -5,2 | 2,1 | -1,7 | -2,7 | 1,3 |
| -22,6 | -17,5 | -6,2 | -3,2 | -2,9 | -0,1 | 0,4 | -1,2 |
| -10,9 | -9,3 | -1,6 | 1,5 | 0,2 | -0,9 | -0,6 | -0,1 |
| -7,1 | -1,9 | 0,2 | 1,5 | 0,9 | -0,1 | 0,3 | |
| -0,6 | -0,8 | 1,5 | 1,6 | -0,1 | -0,7 | 0,6 | 1,3 |
| 1,8 | -0,2 | 1,6 | -0,3 | -0,8 | 1,5 | -1 | |
| -1,3 | -0,4 | -0,3 | -1,5 | -0,5 | 1,7 | 1,1 | -0,8 |
| -2,6 | 1,6 | -3,8 | -1,8 | 1,9 | 1,2 | -0,6 | -0,4 |
Отметим очень интересную особенность полученного DCT-спектра: наибольшие его значения сосредоточены в левом верхнем углу табл. 8.7 (низкочастотные составляющие), правая же нижняя его часть (высокочастотные составляющие) заполнена относительно небольшими числами. Чисел этих, правда, столько же, как и в блоке изображения: 8х8 = 64, то есть пока никакого сжатия не произошло, и, если выполнить обратное преобразование, получим тот же самый блок изображения. Следующим этапом работы алгоритма JPEG является квантование (табл. 8.8).
Таблица 8.8
Процесс квантования
| Ранее полученный результат DCT | |||||||
| 235,6 | -1 | -12,1 | -5,2 | 2,1 | -1,7 | -2,7 | 1,3 |
| -22,6 | -17,5 | -6,2 | -3,2 | -2,9 | -0,1 | 0,4 | -1,2 |
| -10,9 | -9,3 | -1,6 | 1,5 | 0,2 | -0,9 | -0,6 | -0,1 |
| -7,1 | -1,9 | 0,2 | 1,5 | 0,9 | -0,1 | 0,3 | |
| -0,6 | -0,8 | 1,5 | 1,6 | -0,1 | -0,7 | 0,6 | 1,3 |
| 1,8 | -0,2 | 1,6 | -0,3 | -0,8 | 1,5 | -1 | |
| -1,3 | -0,4 | -0,3 | -1,5 | -0,5 | 1,7 | 1,1 | -0,8 |
| -2,6 | 1,6 | -3,8 | -1,8 | 1,9 | 1,2 | -0,6 | -0,4 |
| Таблица квантования | |||||||
| Результат квантования | |||||||
| -1 | |||||||
| -2 | -1 | ||||||
| -1 | -1 | ||||||
Если внимательно посмотреть на полученные в результате DCT коэффициенты, то будет видно, что добрая их половина - нулевые или имеет очень небольшие значения (1 - 2). Это высокие частоты, которые (обычно) могут быть безболезненно отброшены или, по крайней мере, округлены до ближайшего целого значения. Квантование заключается в делении каждого коэффициента DCT на некоторое число в соответствии с матрицей квантования. Эта матрица может быть фиксированной либо, для более качественного и эффективного сжатия, получена в результате анализа характера исходной картинки. Чем больше числа, на которые происходит деление, тем больше в результате деления будет нулевых значений, а значит, сильнее сжатие и заметнее потери.
Совершенно очевидно, что от выбора таблицы квантования будет в значительной степени зависеть как эффективность сжатия – число нулей в квантованном (округленном) спектре,– так и качество восстановленной картинки. Таким образом, мы округлили результат DCT и получили в большей или меньшей степени искаженный поблочный спектр изображения. Следующим этапом работы алгоритма JPEG является преобразование 8х8 матрицы DCT-спектра в линейную последовательность. Но делается это таким образом, чтобы сгруппировать по возможности вместе все большие значения и все нулевые значения спектра. Совершенно очевидно, что для этого нужно прочесть элементы матрицы коэффициентов DCT в порядке, изображенном на рис. 8.5, то есть зигзагообразно - из левого верхнего угла к правому нижнему. Эта процедура называется зигзаг-сканированием.
В результате такого преобразования квадратная матрица 8х8 квантованных коэффициентов DCT превратится в линейную последовательность из 64 чисел, большая часть из которых – это идущие подряд нули. Известно, что такие потоки можно очень эффективно сжимать путем кодирования длин повторений. Именно так это и делается.
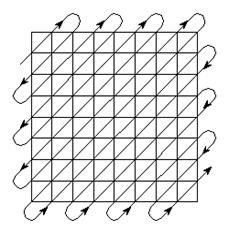
Рис. 8.5. Порядок чтения элементов матрицы коэффициентов
На следующем, пятом этапе JPEG-кодирования получившиеся цепочки нулей подвергаются кодированию длин повторений.
И, наконец, последним этапом работы алгоритма JPEG является кодирование получившейся последовательности каким-либо статистическим алгоритмом. Обычно используется арифметическое кодирование или алгоритм Хаффмена. В результате получается новая последовательность, размер которой существенно меньше размера массива исходных данных.
Последние два этапа кодирования обычно называют вторичным сжатием, и именно здесь происходит неразрушающее статистическое кодирование, и с учетом характерной структуры данных - существенное уменьшение их объема.
Декодирование данных сжатых согласно алгоритму JPEG производится точно так же, как и кодирование, но все операции следуют в обратном порядке.
После неразрушающей распаковки методом Хаффмена (или LZW, или арифметического кодирования) и расстановки линейной последовательности в блоки размером 8х8 чисел спектральные компоненты деквантуются с помощью сохраненных при кодировании таблиц квантования. Для этого распакованные 64 значения DCT умножаются на соответствующие числа из таблицы. После этого каждый блок подвергается обратному косинусному преобразованию, процедура которого совпадает с прямым и различается только знаками в матрице преобразования. Последовательность действий при декодировании и полученный результат иллюстрируются приведенной ниже табл. 8.9.
Таблица 8.9
Последовательность действий при декодировании
| Квантованные данные | |||||||||||||
| -1 | |||||||||||||
| -2 | -1 | ||||||||||||
| -1 | -1 | ||||||||||||
| Деквантованные данные | |||||||||||||
| -10 | |||||||||||||
| -24 | -12 | ||||||||||||
| -14 | -13 | ||||||||||||
| Результат обратного DCT | |||||||||||||
| Для сравнения - исходные данные | |||||||||||||
Очевидно, что восстановленные данные несколько отличаются от исходных. Это естественно, потому что JPEG и разрабатывался, как сжатие с потерями. На представленном ниже рис. 8.6 приведено исходное изображение (справа), а также изображение, сжатое с использованием алгоритма JPEG в 10 раз (слева) и в 45 раз (в центре). Потеря качества в последнем случае вполне заметна, но и выигрыш по объему тоже очевиден.
Итак, JPEG-сжатие состоит из следующих этапов:
– Разбиение изображения на блоки размером 8х8 пикселов.
– Применение к каждому из блоков дискретного косинусного преобразования.
– Округление коэффициентов DCT в соответствии с заданной матрицей весовых коэффициентов.
– Преобразование матрицы округленных коэффициентов DCT в линейную последовательность путем их зигзагообразного чтения.
– Кодирование повторений для сокращения числа нулевых компнент.
– Статистическое кодирование результата кодом Хаффмена или арифметическим кодом.



Рис. 8.6. Вид изображений до и после сжатия
Декодирование производится точно так же, но в обратном порядке.
Существенными положительными сторонами алгоритма сжатия JPEG являются:
– возможность задания в широких пределах (от 2 до 200) степени сжатия;
– возможность работы с изображениями любой разрядности;
– симметричность процедур сжатия – распаковки.
К недостаткам можно отнести наличие ореола на резких переходах цветов - эффект Гиббса, а также распадение изображения на отдельные квадратики 8х8 при высокой степени сжатия.
Фрактальный метод
Фрактальное сжатие основано на том, что изображение представляется в более компактной форме с помощью коэффициентов системы итерируемых функций (Iterated Function System – IFS).
Прежде чем рассматривать сам процесс фрактального сжатия, разберемся, как IFS строит изображение, то есть рассмотрим процесс декомпрессии. Строго говоря, IFS представляет собой набор трехмерных аффинных преобразований, в нашем случае переводящих одно изображение в другое. Преобразованию подвергаются точки в трехмерном пространстве (координата точки изображения X, координата точки изображения Y и яркость точки I). Упрощенно этот процесс можно пояснить следующим образом. Рассмотрим так называемую фотокопировальную машину (рис. 8.7), состоящую из экрана, на котором изображена исходная картинка, и системы линз, проецирующих изображение на другой экран. Фотокопировальная машина может выполнять следующие действия:
– линзы могут проецировать часть изображения произвольной формы в любое другое место нового изображения;
– области, в которые проецируются изображения, не пересекаются;
– линза может менять яркость и уменьшать контрастность;
– линза может зеркально отражать и поворачивать свой фрагмент изображения;
– линза должна масштабировать (уменьшать) свой фрагмент изображения.

Рис. 8.7. Установка, поясняющая принцип фрактального метода
Расставляя линзы и меняя их характеристики, можно управлять получаемым изображением. Одна итерация работы машины заключается в том, что по исходному изображению с помощью проектирования строится новое, после чего новое берется в качестве исходного. Утверждается, что в процессе итераций мы получим изображение, которое перестанет изменяться. Оно будет зависеть только от расположения и характеристик линз и не будет зависеть от исходной картинки. Это изображение называется “неподвижной точкой”, или аттрактором данной IFS. Соответствующая теория гарантирует наличие ровно одной неподвижной точки для каждой IFS.
Поскольку отображение линз является сжимающим, каждая линза в явном виде задает самоподобные области в нашем изображении. Благодаря самоподобию получаем сложную структуру изображения при любом увеличении. Таким образом, интуитивно понятно, что система итерируемых функций задает фрактал – самоподобный математический объект.
| Наиболее известным из изображений, полученных с помощью IFS, является так называемый“папоротник Барнсли” (рис. 8.8), задаваемый четырьмя аффинными преобразованиями (или, в нашей терминологии, “линзами”). Каждое преобразование кодируется буквально считанными байтами, в то время как изображение, построенное с их помощью, может занимать и несколько мегабайт. На этом изображении можно выделить 4 области, объединение которых покрывает все изображение и каждая из которых подобна всему изображению (не забывайте о стебле папоротника). |  Рис. 8.8. “Папоротник Барнсли”
Рис. 8.8. “Папоротник Барнсли”
|
Из вышесказанного становится понятно, как работает фрактальный кодер, и также очевидно, что для сжатия ему понадобится очень много времени.
Фактически фрактальная компрессия – это поиск самоподобных областей в изображении и определение для них параметров аффинных преобразований. Для этого потребуется выполнить перебор и сравнение всех возможных фрагментов изображения разного размера.
Даже для небольших изображений при учете дискретности мы получим астрономическое число перебираемых вариантов, причем даже резкое сужение классов преобразований, например, за счет масштабирования, только в определенное количество раз не дает заметного выигрыша во времени. Кроме того, при этом теряется качество изображения. Подавляющее большинство исследований в области фрактального сжатия сейчас направлены на уменьшение времени архивации, необходимого для получения качественного изображения.
Дата добавления: 2016-02-04; просмотров: 1262;
