Линейчатый спектр атома водорода

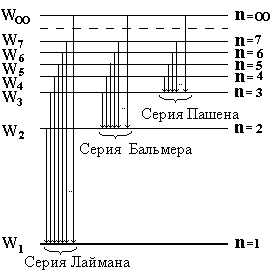Рис. 2.1

Спектром называют совокупность (сплошная, дискретная) монохроматических колебаний, излучаемых или поглощаемых каким-либо телом.

Любые светящиеся газы дают линейчатые спектры испускания. Изучая линейчатые спектры атома водорода, Бальмер получил формулу 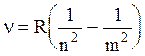, (2.1)

где m и n - квантовые числа; n - частота испущенного (поглощенного) кванта;

R = 3,29×10¹⁵ с^-1 - постоянная Ридберга.

Ридберг показал, что в линейчатых спектрах не только атома водорода, но и атомах других элементов наблюдаются спектральные серии. В частности, для водорода из множества серий можно выделить спектральные серии (рис. 2.1): I. серия Лаймана (ультрафиолетовый спектр) 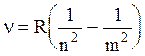, где n = 1, m = 2, 3, 4, ... . II. серия Бальмера (видимый спектр) 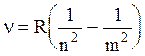, где n =2, m =3, 4, 5, ... .III. серия Пашена (инфракрасный спектр) 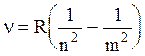, где n=3, m=4, 5,.… и т. д.

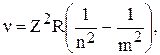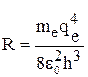В спектре поглощения водорода наблюдается только серия Лаймана, т. к. она соответствует квантовым переходам атома из основного состояния в другие возбужденные. Спектральные частоты водородоподобных ионов можно найти по формуле где ; Z - порядковый номер в периодической системе элементов Д. И. Менделеева.

Следовательно, спектральные серии водородоподобных ионов смещаются относительно спектральных серий атома водорода.

При соединении атомов в молекулы и кристаллы внешние оболочки атомов сильно искажаются, поэтому оптические и инфракрасные спектры молекул являются полосатыми, а металлов сплошными.

Атом можно возбудить и путем удаления одного из электронов внутренней заполненной оболочки. На электрон глубокой оболочки в основном действует кулоновское притяжение ядра, лишь слегка экранированное другими электронами. Это экранирование учитывается заменой заряда ядра на (Z - s)e, где s - поправочный коэффициет (s << Z) и различен для глубоких оболочек.

В этом случае частота излучения при переходах на глубокие оболочки определяется по формуле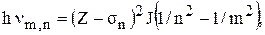

где J – постоянная (ионизационный потенциал).

Серии излучения лежат в рентгеновской области электромагнитного спектра. Наблюдаемое при электронных переходах на глубокие уровни атома рентгеновское излучение называют характеристическим, поскольку это излучение зависит от энергетического спектра электронов в атоме.

Для отдельной серии, т. е. при фиксированном n частота излучения находится по формуле (закон) Мозли 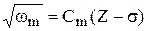, где С_m - постоянная.

Закон Мозли позволяет по частотам характеристического рентгеновского излучения атомов устанавливать их номера, что сыграло положительную роль при определении мест элементов в периодической системе Д. И. Менделеева.

Постулаты Бора

Для объяснения устойчивости атомов, их линейчатых спектров и других свойств атомов Бор предложил использовать постулаты:

1) . Существует стационарные состояния атома, находясь в котором он не излучает энергии.

2) . В стационарном состоянии атома электрон, двигаясь по круговой орбите, должен иметь квантованное значение момента импульса, т.е.

L_n= mvr = n 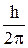, (2.2)

где m - масса электрона; v - его скорость; r - радиус орбиты; h - постоянная Планка.

Как показала квантовая теория, n = 1, 2, 3, ... , - главное квантовое число, характеризует энергетические уровни атомов.

3) . При переходе электрона в атоме с высшего возбужденного энергетического уровня W_m на низший W_n испускается квант энергии

e = hn_mn= DW = W_m - W_n. (2.3)

При поглощении кванта энергии e = hn_mn атомом электрон переходит с энергетического уровня W_n на энергетический уровень W_m .

Уровень n = 1 - основной, невозбужденный уровень; уровни n = 2, 3, 4, ... , - возбужденные уровни.

Первый потенциал возбуждения атома .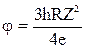

Полная энергия электрона в атоме

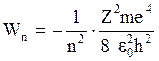, (2.4)

где m - масса электрона; e₀ - электрическая постоянная. При n ® ¥, W_n ® 0.

Абсолютное значение W_n в формуле (2.4) называют энергией связи электрона в атоме, находящегося в состоянии n.

Поэтому уровень 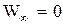соответствует энергии ионизации атома водорода, т. е. отрыву электрона. Энергию ионизации атома связывают с потенциалом ионизации j, т. е. W_ион= |е|j|. (2.5)

Частоту n излученного (поглощенного) кванта находят по формуле (2.1).

Для атома водорода при n = 1 потенциал ионизации j = 13,53 В,

W₁= = -2,16×10^-18 Дж = - 13,53 эВ.

Радиусы боровских орбит электрона в водородоподобных атомах можно вычислить по формуле ,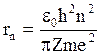

где e₀ – электрическая постоянная; h – постоянная Планка; n – главное квантовое число; Z – порядковый номер в периодической системе элементов Д. И. Менделеева; m - масса электрона; е – элементарный заряд.

Первый боровский радиус электрона, который характеризует в среднем размер атома водорода r₁ @5,29×10^-11 м. Размер атома определяется его электронной оболочкой. Скорость обращения электрона по боровской орбите вычисляют по формуле 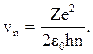Для атома водорода скорость электрона на 1- й боровской орбите v₁ = 2,2×10⁶ м/с (n = 1).