Упругие волны. Скорость и энергия упругой волны.

Скорость упругой волны.

Рассмотренные нами волны в цепочке очень хорошо представляют сущность волновых процессов во всевозможных телах (стержнях, струнах и т.д.) или в сплошных средах (твердых, жидких и газообразных). В твердых телах возможны как продольные, так и поперечные волны. В жидких и газообразных, не имеющих упругости формы (модуль сдвига равен нулю) поперечные волны невозможны, возможны только продольные. При распространение волны в такой среде создаются чередующиеся сгущения и разрежения частиц, перемещающиеся в направлении распространения волны.

Найдем скорость волны в тонком стержне. Под тонким имеется в виду стержень, толщина которого мала по сравнению с длиной волны λ. При малых продольных деформациях стержня спра­ведлив закон Гука:

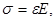(3.2.1)

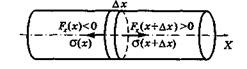где σ= 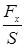— напряжение (Н/м²), Ε — модуль Юнга (Па), ε = дξ/дх – относительная деформация. Заметим, что σ, как и ε, величина алгебраическая, и знаки σ и ε всегда одинаковы: при растяжении — положительные, при сжатии — отрицательные.

Рассмотрим малый элемент стержня Δx « λ в момент, Рис.3.2.1.

когда при прохождении волны (длина волны )

он оказался, например, в растянутом состоянии (рис.3.2.1). Применим к этому элементу 2-й закон Ньютона:

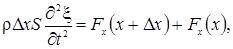
где ρ — плотность материала стержня, S — площадь его попе­речного сечения. В данный момент, как видно из рисунка, F_x(x + ∆х) > 0, a F_x(x) < 0. Соответствующие же значения σ в сечениях x и x + Δx положительные (растяжение). Поэтому правую часть уравнения можно переписать так:

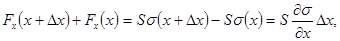
где учтено, что слева F_x и σ имеют разные знаки (это будет и при сжатии). Тогда уравнение движения после сокращения на Δx·S примет вид 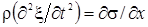. Остается учесть (3.2.1), после чего получим окончательно:

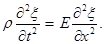(3.2.2)

Мы пришли, таким образом, к волновому уравнению. Это по­зволяет утверждать, что в стержне будет распространяться про­дольная волна, скорость которой легко определить, сопоста­вив полученное выражение с (3.1.10):

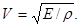(3.2.3)

Заметим, что для не тонкого стержня выражение для V име­ет более сложный вид и значение V оказывается больше, чем в случае тонкого стержня.

Можно показать, что скорость упругих поперечных волн в неограниченной изотропной твердой среде

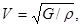(3.2.4)

где G — модуль сдвига среды, ρ — ее плотность.

Скорость звука в жидкостях и газах.

Формулу (3.2.3) можно использовать для вычисления скорости продольных волн в жид­костях и газах, в частности, звуковых волн, которые являются упругими волнами определенного частотного диапазона (20 ÷ 20000 Гц). Действительно, вырезав мысленно канал в на­правлении распространения плоской волны, мы можем повто­рить все рассуждения, приведшие нас к этой формуле. Остается только выяснить, какая величинав этом случае играет роль модуля Юнга Е.

При продольных волнах в среде возникают сжатия и разрежения отдельных слоев, и закон Гука (3.2.1) в данном случае — связь избыточного давления Δр сотносительным изменением длины элемента Δх цилиндрического канала Δξ/Δx — примет вид Δp = - ΕΔξ/Δx, где знак минус связан с тем, что приращения давления Δp и длины Δξ противоположны по знаку. Умножив числитель и знаменатель на площадь поперечного сечения ка­нала, получим

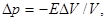(3.2.5)

где ΔV/V — относительное приращение объема рассматривае­мого элемента. Перейдя к пределу, получим

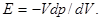(3.2.6)

Объем V элемента Δx и его плотность меняются при прохожде­нии волны, но их произведение, т. е. масса т= ρV = const. Отсюда dρ/ρ = -dV/V, значит

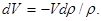(3.2.7)

После подстановки этого выражения в (3.2.6) получим Ε = 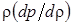, и скорость волны — формула (3.2.3) — примет вид

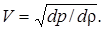(3.2.8)

Это выражение справедливо для волн в жидкостях и газах.

Опыт показывает, что при распространении звука в газе связь между давлением и объемом определяется уравнением

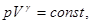(3.2.9)

где γ — так называемая постоянная адиабаты, равная отноше­нию теплоемкостей газа при постоянных давлении и объеме, γ = C_P/C_V — величина, характерная для каждого газа. Запишем дифференциал натурального логарифма выражения (3.2.9):

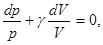
откуда dp/dV = - γp/V, и формула (3.2.3) принимает вид

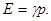(3.2.10)

Таким образом, скорость звуковой волны в газе

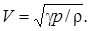(3.2.11)

Это выражение можно преобразовать к более удобному для рас­четов виду, если учесть уравнение состояния идеального газа pV = (m/M)RT, где, напомним, m — масса газа, Μ — его мо­лярная масса. Из уравнения состояния определим плотность как ρ = m/V = pM/RT, и уравнение (3.2.11) станет таким:

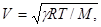(3.2.12)

где R — универсальная газовая постоянная.

Энергия волны. Плотность потока энергии. Интенсивность волны.

Прежде всего, найдем вы­ражение для плотности упругой (потенциальной) энергии рас­тянутого (или сжатого) стержня. Приложим к торцу стержня, другой конец которого закреплен, растягивающую силу F(x) и будем медленно увеличивать ее от 0 до значения F₀. Удлинение стержня при этом будет меняться от 0 до x. По закону Гука F(x) = κх, где κ — коэффициент упругости. Работа силы F(x) в этом процессе

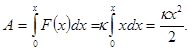
Эта работа идет на увеличение упругой энергии U стержня, значит

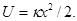(3.2.13)

Плотность же упругой энергии w_n = U/Sl, где S и l — пло­щадь поперечного сечения и длина стержня. Преобразуем вы­ражение (3.2.13), учитывая, что k 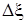= F = σS, σ = Εε и ε = 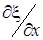. Тогда

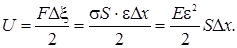
Отсюда видно, что плотность упругой энергии

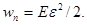(3.2.14)

При прохождении продольной волны в стержне каждая еди­ница объема его обладает как потенциальной энергией упругой деформации w_π,так и кинетической энергией w_{k= 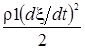.}Плотность полной энергии

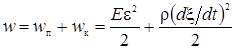. (3.2.15)

Для тонкого стержня Ε = ρV², согласно (3.2.3), и выражение (3.2.15) можно переписать так:

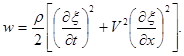(3.2.16)

Можно показать, что оба слагаемых равны друг другу, т. е. плотности кинетической и упругой энергии оди­наковы и изменяются синфазно. Поэтому мы имеем в результате

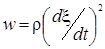(3.2.17)

В частности, для гармонической волны 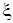= 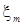cοs(ωt - kx)

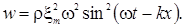(3.2.18)

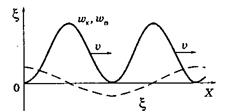
Соответствующее распределение w(x) вдоль стержня в некото­рый момент показано на рис.3.2.2.

Среднее значение плотности энергии за период (или за время значительно большее периода колебаний) равно Рис.3.2.2.

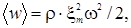(3.2.19)

поскольку среднее значение квадрата синуса равно ½.

Полученные формулы справедливы и для упругих волн в жидкостях и газах.

Плотность потока энергии.

Так как энергия перемещается в среде вместе с возмущением, вводят понятие потока энергии Ф. Это количество энергии, переносимое волной через определен­ную поверхность S в единицу времени:

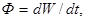(3.2.20)

где dW — энергия, переносимая через данную поверхность за время dt.

Поток энергии в разных точках поверхности S может иметь различную интенсивность. Для характеристики этого обстоя­тельства вводят понятие плотности потока энергии. Это по­ток энергии через единичную площадку, перпендикулярную к направлению переноса энергии:

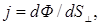(3.2.21)

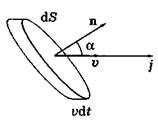где dФ = dW/dt, a dW — это энергия, заключенная внутри косого цилиндра с основанием площадью dS и образующей длиной Vdt, где V — ско­рость переноса энергии (или скорость волны). Размеры этого цилиндра должны быть настолько малы, чтобы во всех его точ­ках плотность энергии w была бы оди­наковой. Тогда dW = wdV, dV— объем данного цилиндра, и мы можем записать: Рис.3.2.3.

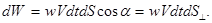
С учетом этого соотношения выражение (3.2.21) примет вид:

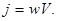(3.2.22)

Для определения плотности потока и его направления вводят вектор Умова- Пойнтинга :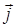

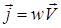(3.2.23)

где 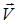— вектор скорости, нормальный к волновой поверхности в данном месте. Для гармонической волны 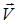= (ω/k) .

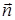В случае монохроматической волны вектор 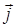, как и плот­ность энергии, изменяется со временем по закону квадрата си­нуса (3.2.18). Поэтому среднее по времени значение модуля вектора Умо­ва - Пойнтинга с учетом (3.2.19) можно записать как

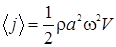(3.2.24)

Это выражение справедливо для волн любого вида — плоской, сферической, цилиндрической, затухающих и др.

Среднее по времени значении модуля плотности потока энергии на­зывают интенсивностью волны: I=<j>.

Зная вектор Умова - Пойнтинга во всех точках интересующей нас поверх­ности S, можно найти поток энергии сквозь эту поверхность. Для этого разобьем мысленно поверхность S на элементарные участки dS. Поток энергии через этот участок, согласно (3.2.21), есть

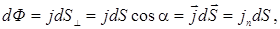
где j_n — проекция вектора 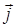на нормаль 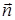к элементу поверхности dS. Тогда полный поток энергии сквозь поверхность S

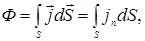(3.2.25)

здесь 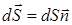. Выражение (3.2.25) означает, что поток энергии равен потоку вектора 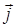сквозь эту поверхность S.

Стоячие волны.

. При распространении в упругой среде одновременно нескольких волн возникает их наложение, причем волны не возмущают друг друга: колебания частиц среды оказываются векторной суммой колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности. Это называют принципом суперпозиции (наложения) волн.

Рассмотрим практически важный случай, когда две гармо­нические волны с одинаковыми частотой ω и амплитудой 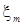рас­пространяются в противоположных направлениях оси х :

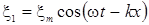
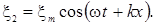
Чтобы не усложнять формулы, начала отсчета времени и коор­динаты выбраны так, чтобы начальные фазы для обеих волн были рав­ны нулю.

Суперпозиция этих волн дает:

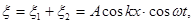где A= 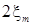. (3.2.26)

Это и есть уравнение стоячей волны. Видно, что ее частота та же, т.е. ω, а амплитуда равна (Acoskx) и, в отличие от бегущей гар­монической волны, зави 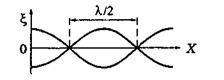сит от x. В точках, где |coskx| = l, мы имеем максимумы — пучности, а где coskx = 0 —

минимумы — узлы. Период |coskx| равен π, поэтому kΔx = π и Δх = π/k = λ/2. Т. е. интервалы между соседними пучностями или узлами равны Рис.3.2.4.

половине длины волны (см. рисунок 3.2.4,где показаны крайние смеще­ния ξ через половину периода).

Между двумя соседними узлами все точки среды колеблют­ся синфазно, при переходе же через узел фаза изменяется на π, т. е. колебания по разные стороны от узла (в пределах полуво­лны) происходят в противофазе. Узлы смещения как бы разде­ляют среду на автономные области, в которых гармонические колебания совершаются независимо. Никакой передачи движе­ния из одной области к другой, а значит и перетекания энергии через узлы не происходит. Другими словами, нет никакого рас­пространения возмущения вдоль оси х. Именно поэтому возму­щения, описываемые формулой (3.2.26), и называют стоячей волной.

Энергия стоячей волны.

Переходя к распределению энергии в стоячей волне, определим сначала с помощью (3.2.26) выраже­ние для скорости 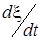частиц среды и ее относительной деформа­ции ε = dξ/dx:

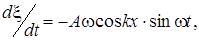
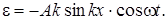(3.2.27)

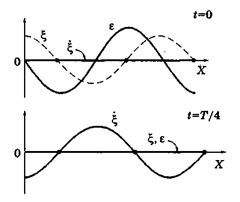Видно, что обе величины, 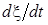и ε, тоже стоячие волны, причем они сдвинуты относительно друг друга по фазе на π/2 — как в пространстве, так и во времени. Кроме того, узлы и пучности скорости 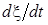частиц среды совпадают с узлами и пучностями их смещения ξ. Узлы же и пучности деформации ε совпадают со­ответственно с пучностями и узлами смещения. Это показано на рисунке для моментов t = 0 и t = Т/4, здесь узлы смещения отмечены жирными точками. В момент t = 0, когда ξ и ε ста­новятся максимальными, скорость обращается Рис.3.2.5.

в нуль, и на­оборот (t = T/4).

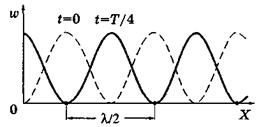Соответственно происходят превращения энергии стоячей вол­ны: то полностью в потенциальную (упругую), то полностью в ки­нетическую (аналогичное происходит при колебаниях маятника). На рис. 3.2.6 показано распределение плотности энергии в моменты t = 0 и t = T/4. В процессе колебаний происходит перетекание энергии от каждого узла к соседним с ним Рис.3.2.6.

пучностям и обратно. Средний же по времени поток

энергии в любом сечении стоячей волны равен нулю.

Лекция 3.3.