МОДЕЛИРОВАНИЕ НЕКОТОРЫХ СИСТЕМ, СВОДИМЫХ К ОБЫКНОВЕННЫМ ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ

Справка: Программа решения системы дифференциальных уравнений

методом Рунге-Кутта 4-го порядка.

Dim у(1 to 10) As Single

Dim a(1 to 10) As Single

Dim k(1 to 10) As Single

Dim f(1 to 10) As Single

Dim w(1 to 10) As Single

Sub Runge()

z=InputBox ("число уравнений")

n=CInt(z)

z=InputBox("шаг")

h=CSng(z)

for j=l to n

I=MsgBox (J, 0, "задайте начальное значение y(0)")

z=InputBox ("y(0)")

w(j)=CSng(z)

y(j)=w(j)

next j

133 call func

for j=1 to n

v=h*f(j)

k(j)==v; y(j)=w(i)+v/2

next j: call funk for j=1 to n v=h*f(j)

k(j)+2*v: y(j)=w(j)+v

next j

x=x+h/2

I=MsgBox (x, 1, "для x=") call funk for j=1 to n

y(j)=w(j)+(k(j)+h*0))/6

i=MsgBox(y(j), 1, "Значение функции=')

w(j)=y(j)

next j

goto 133

end Sub 'Runge

_______________________________________

Sub funk()

f(1)=y(2)

f(2)=(y(1)/x-y(2))/x-y(1)

end Sub

_______________________________________

Тестовый пример:

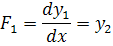
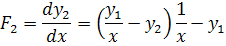
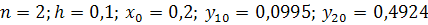
Соотношения метода Рунге - Кутта 4-го порядка:

________________________________________

)

________________________________________

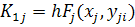
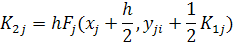
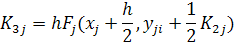
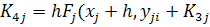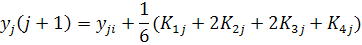
Решение дифференциального уравнения первого порядка

С разделяющими переменными на примере модели роста

Популяции

(Логистическая модель Мальтуса-

Ферхюльста)

Математическая формулировка модели

dN/dt=mN(K-N)/K, где N=N(t) -текущая численность популяции, m –относительный коэффициент прироста, К -предельная численность

популяции.