Моделирование движения во вращающейся системе координат (учет
Моделирование движения во вращающейся системе координат (учет силы Кориолиса)[2]
Находясь на вращающейся с угловой скоростью ω горизонтальной платформе в некоторой точке с координатами А(х,у), бросают тело в некотором направлении со скоростью 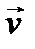 :
:
Найти траекторию тела относительно платформы при различных значениях
(х, у), 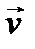 и
и 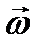 . Силу тяжести и силу трения не учитывать (кусок льда скользит по гладкой платформе).
. Силу тяжести и силу трения не учитывать (кусок льда скользит по гладкой платформе).
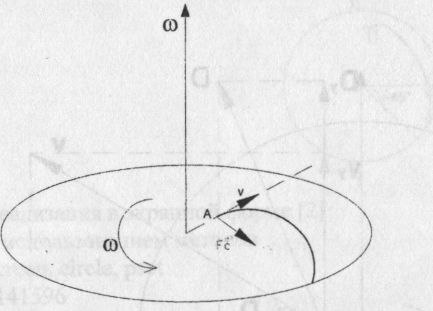
Платформа является вращающейся, т.е. неинерциальной системой отсчета, и на тело действуют две силы инерции:
1) центробежная сила инерции 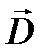 , которая определяется расстоянием от оси вращения R: D = mw2R;
, которая определяется расстоянием от оси вращения R: D = mw2R;
2) сила Кориолиса Fc, которая определяется относительной скоростью (т.е. скорость тела относительно неинерциальной системы) Fc = 2m 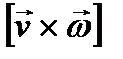 (не путать! v ≠ωR).
(не путать! v ≠ωR).
Центробежная сила D направлена по радиусу от центра: ее составляющие:
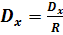
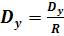
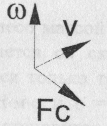
Сила Кориолиса 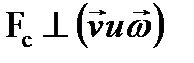 .
.
При вращении платформы в указанном направлении 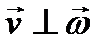 и Fc
и Fc
направлена 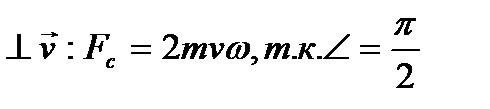 .
.
Составляющие силы Кориолиса: 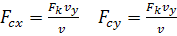
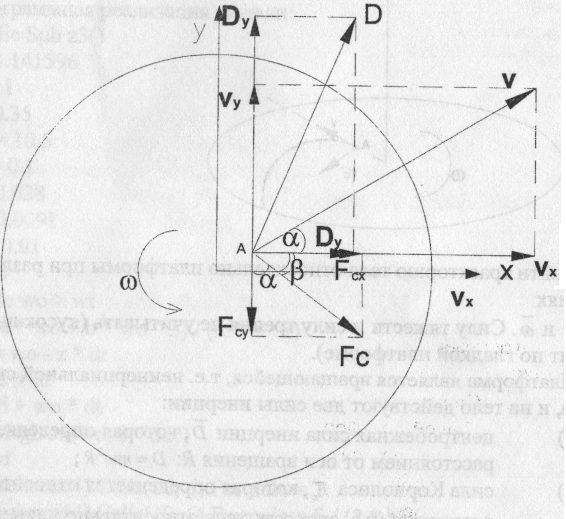
Уравнения движения:
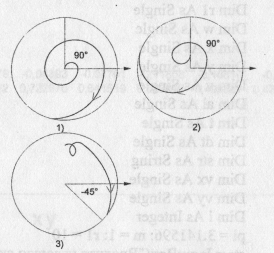
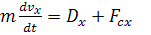 1) х=у=0; v=10 м/с; а=90°;
1) х=у=0; v=10 м/с; а=90°;
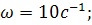
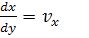 2) х=0; у=1м; v=10 м/с; а=90 °;
2) х=0; у=1м; v=10 м/с; а=90 °;
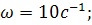
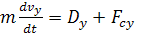 3) х=0; у=5м; v=20 м/с; а=-45 °;
3) х=0; у=5м; v=20 м/с; а=-45 °;
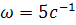
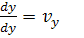
rem Реализация в экранной форме [2]
rem с использованием методов
rem screen, circle, pset
pi=3.141596
m=1: rl=10:g=9.8
Rem Ввод: w, x, y, v, al
a1=a1*pi/180
t=0: t1=1e-3
vx=v*cos(al)
vy=v*sin(al)
screen 8
circle (300, 100), r1*20,3
met1: x=x+vx*t1: y=y+vy*tl: r=sqr(x*x+y*y)
d=m*w*w*r: dx=d*x/r: dy=d*y/r
fc=2*m*v*w: fcx=fc*vy/v: fcy=-fc*vx/v
vx=vx+(fcx+dx)*t1 /m
vy=vy+(fcy+dy) * t1 /m
v=sqr(vx*vx+vy*vy)
x1=x*20+300: y1=100-y*20*0.4
pset(x1,y1),4
if sqr(x*x+y*y)>rl then goto met2
goto met1
met2: end
rem Реализация в среде VBA
Sub platforma()
Dim pi As Single
Dim m As Single
Dim rl As Single
Dim w As Single
Dim x As Single
Dim у As Single
Dim v As Single
Dim al As Single
Dim t As Single
Dim dt As Single
Dim str As String
Dim vx As Single
Dim vy As Single
Dim i As Integer
pi = 3.141596: m=1: r1 = 10
str = InputВох("Введите угловую скорость w")
w = CSng(str)
str = InputВох("Введите координату x")
x = CSng(str)
str = InputВох("Введите координату у")
y = CSng(str)
str = InputВох("Введите скорость v")
v = CSng(str)
str = InputВох("Введите угол al")
a1 = CSng(str)
a1 = a1*pi/180
t = 0:dt = 0.005: i = 2
vx = v * Cos(al): vy = v * Sin(al)
met1: x = x + vx * dt: у = у + vy * dt
r = Sqr(x * x + у * у)
d = m*w*w*r 'сила инерции
dx = d*x/r:dy = d*y/r
fc = 2*m*v*w 'сила Кориолиса
fcx = fc * vy / v: fey = -fc * vx / v
vx = vx + (fcx + dx) * dt / m
vy = vy + (fey + dy) * dt / m
x = x + vx * dt: у = у + vy * dt
Worksheets(1).Cells(1, 1). Value = "x"
Worksheets(1).Cells(2, 2).Value = "y"
i = i+ 1
Worksheets(1).Cells(l, i).Formula = x
Worksheets(1).Cells(2, i).Formula = у
v = Sqr(vx * vx + vy * vy)
'x1 = x * 20 + 300: y1 = 100 - у * 20 * 0.4
Ifr>r1 Then GoTo met2
GoTo met1
met2:
End Sub
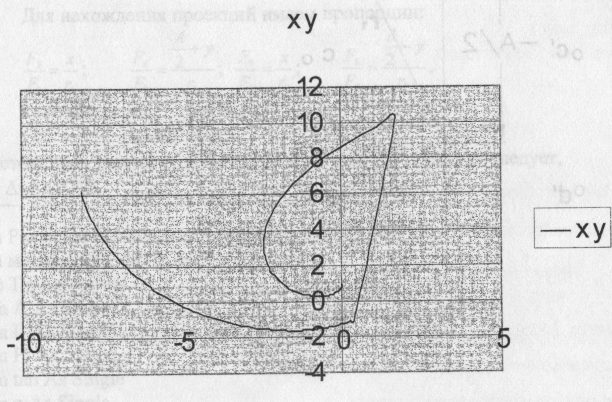
x -0 005 -0,01979 -0,04393 -0,07701 -0,11858 -0,16819 -0,2254
у 0,902375 0,809762 0,722676 0,641619 0,567077 0,499527 0,439437
Моделирование траекторий электронов[2]
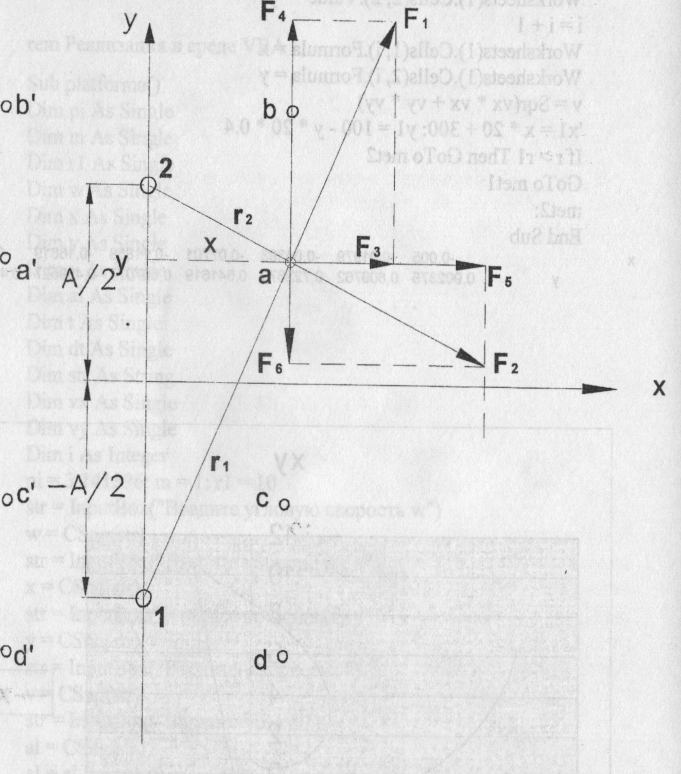
А=2 мм;
τ=-4·10-9Кл/м.
В плоскости М на расстоянии А друг от друга лежат две положительно заряженные тонкие проволоки с линейной плотностью заряда т в направлении, перпендикулярном к этой плоскости, с расстояния L приближается электрон с начальной скоростью v. Какие возможные траектории он создает при различных v, τ, р(прицельное расстояние)?
Алгоритм
Помещаем начало координат в середине между проволоками 1 и 2. Выбираем исходную точку а при х>0 и, пользуясь формулой
напряженности 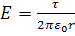 и принципом суперпозиции, ищем силы, действующие на электроны, и их проекции.
и принципом суперпозиции, ищем силы, действующие на электроны, и их проекции.
Составляем уравнение движения.
Исходим из требования, что время пролета 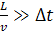 - приращения
- приращения
времени.
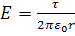 ; сила F = Eq
; сила F = Eq
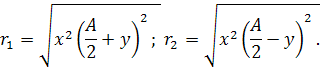
Для нахождения проекций имеем пропорции:
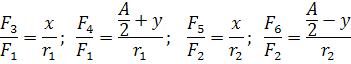
Рекомендации: p~0,6 мм;
Vx*107m/c.
Расстояние L, равное А, будет пройдено и за ≈10-9 с, откуда следует, что 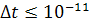 с.
с.
rem Реализация в экранной форме (среда VB)[2]
rem методы line, circle, pset
Sub Траектории()
Dim A As Single
Dim L As Single
Dim Pi As Single
Dim tan As Single
Dim q As Single
Dim e0 As Single
Dim p0 As Single
Dim m As Single
Pi=3.141596
q=-1.6E-19: e0=8.85E-12: m=9.1E-31
dt=2E-11: k=5E3: p0=2E-3
for p=p0 to 10*p0 step p0
vx=1E-7: vy=0: x=-L: y=p
Line(0,150)-(400,150),3
Circle(L*k,150-A/2*k*0.3),2,3
Circle(L*k, 150+A/2*k*0.3),2,3
For t=0 to 5E-8 step dt
r1=Sqr(x*x+(A/2+y)^2)
r1=Sqr(x*x+(A/2-y)^2)
z=tau*q/(2*pi*e0): f1=z/r1: f2=z/r2
G=f1*x/r1: f4=n*(A/2+y)/r1
f5=f2*x/r2: f6=f2*(A/2+y)/r2
wx=(D+f5)m: wy=(f4-f6)/m
vx=vx+wx*dt: vy=vy+wy*dt
x=x+vx*dt: y=y+vy*dt
xe=(x+L)*k: ye=150-y*k*0.3
if xe<0 then goto kon
if xe>500 then goto kon
if ye<0 then goto kon
if ye>500 then goto kon
Pset (xe, ye), 4
next t
kon: next p
end Sub ' Траектория
Моделирование магнитного поля[2]
Напряженность магнитного поля 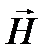 , создаваемая током
, создаваемая током 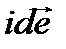 в точке А на
в точке А на
расстоянии 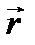 от
от 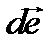 по закону Био-Савара-Лапласа:
по закону Био-Савара-Лапласа:
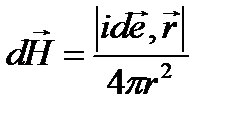 , где направление
, где направление 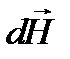 по правилу правого
по правилу правого
винта. Магнитное поле витка. Найдите напряженность магнитного поля плоского витка радиусом R с силой тока I=1 А в центре и на расстоянии а от центра в плоскости витка.
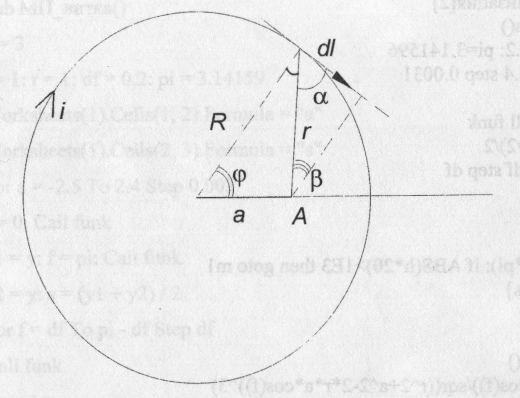
Указание: свести выражение для dH к одной переменной φ, проинтегрировать от φ=0 до π и удвоить результат. Предусмотреть переход к новой точке А (пройти от а=0 до a=R).
Из рис. 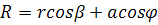 ;
;
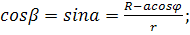
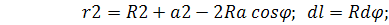
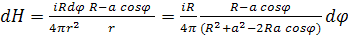
Все слагаемые dH имеют одно направление
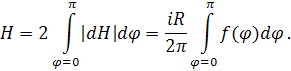
В программе φ=f.
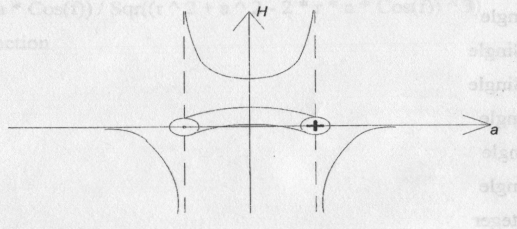
Ответ: график.
rem VB - реализация[2]
Sub МПВитка()
j=l : r=1 : df=0.2 : pi=3.141596
for a=-2.4 to 2.4 step 0.0031
f=0: call funk
y1=y: f=pi: call funk
y2=y: s=(y1+y2)/2
for f=df to pi-df step df
call funk
s=s+y
next f
h=j*r*s*df/(2*pi): if ABS(h*20)>1E3 then goto m1
rem {рисовать}
m1: next a
end Sub
Function funk()
funk:y=(r-a*cos(f))/sqr((r^2+a^2-2*r*a*cos(f))^3)
end function
rem Реализация в среде VBA
Dim j As Single
Dim r As Single
Dim f As Single
Dim df As Single
Dim pi As Single
Dim a As Single
Dim yl As Single
Dim y2 As Single
Dim у As Single
Dim s As Single
Dim h As Single
Dim n As Integer
Sub МП_витка()
n = 3
j = 1: r= 1: df = 0.2: pi = 3.14159
Worksheets(l).Cells(l, 2).Formula = "a"
Worksheets(l).Cells(2, 3).Formula = "s"
For a = -2.5 To 2.4 Step 0.003
f = 0: Call funk
y1 = y: f = pi: Call funk
y2=y:s = (y1+y2)/2
For f=df To pi-df Step df
Call funk
s = s + y
Nextf
h=j*r*s*df/(2*pi)
If Abs(h * 20) > 1000# Then GoTo metka
Worksheets(1).Cells(n, 2).Formula = a
Worksheets(1).Cells(n, 3).Formula = s
n = n+ 1
metka: Next a
End Sub
Function funk()
у = (r - a * Cos(f)) / Sqr((r ^2 + a^2-2*r*a* Cos(f))^3)
End Function
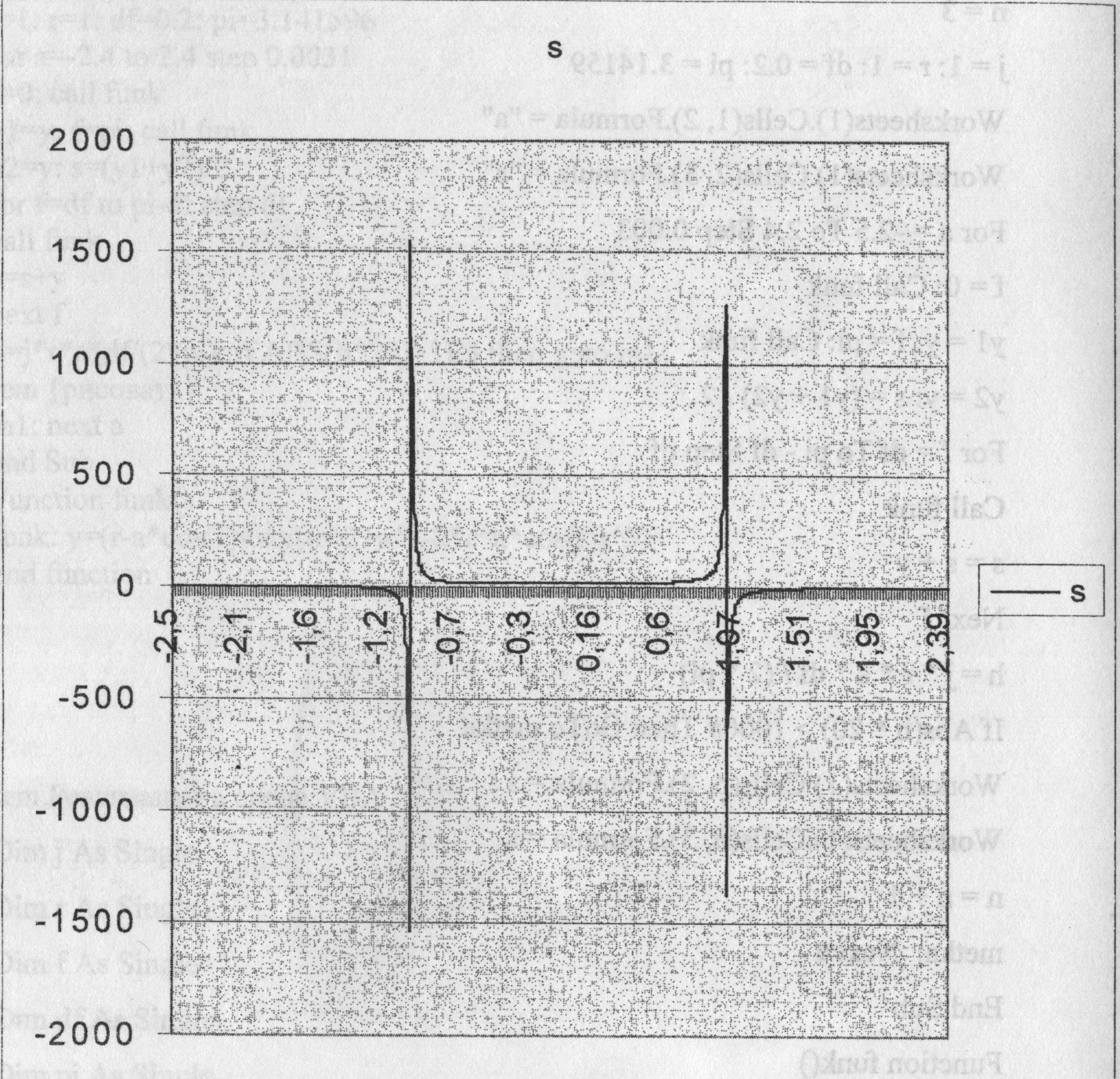
A s
| -2,5 | -0,31745 |
| -2,497 | -0,31883 |
| -2,494 | -0,32022 |
| -2,491 | -0,32162 |
| -2,488 | -0,32303 |
| -2,485 | -0,32445 |
| -2,482 | -0,32587 |
| -2,479 | -0,3273 |
| -2,476 | -0,32874 |
| -2,473 | -0,33019 |
| -2,47 | -0,33165 |
-2,467 -0,33311
-2,464 -0,33458
-2,461 -0,33607
-2,458 -0,33756
-2,455 -0,33905
-2,452 -0,34056
-2,449 -0,34208
-2,446 -0,3436
-2,443 -0,34513
-2,44 -0,34668
-2,437 -0,34823
-2,434 -0,34979
-2,431 -0,35136
-2,428 -0,35293
-2,425 -0,35452
-2,422 -0,35612
-2,419 -0,35772
-2,416 -0,35934
-2,413 -0,36096
-2,41 -0,3626
Геометрическая оптика[2]
Каково расстояние от наблюдателя до оазиса в пустыне, если путник утром видит в небе мираж под углом 10° к горизонту, а показатель преломления из-за сильного охлаждения поверхности пустыни за ночь убывает с высотой z по закону:
n=n0-kz, где n0=1,0004, к=2-10-5 м-1.
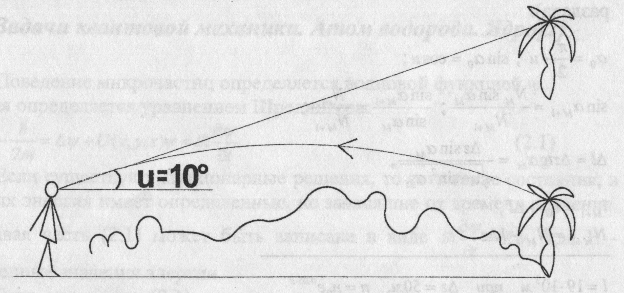
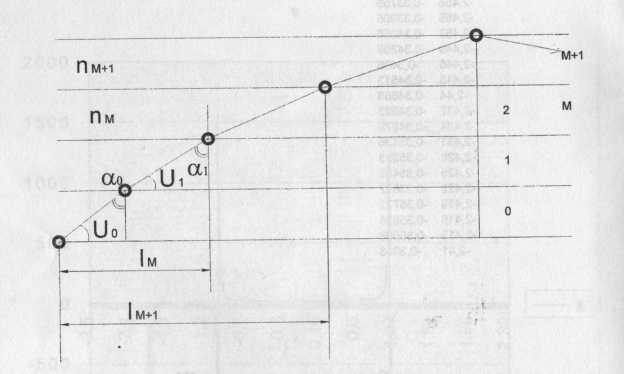
Нужно написать соотношение для перехода от слоя к слою и найти А1 (переход к 1) суммированием, делая маленький шаг 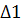 .
.
Так как показатель преломления убывает с высотой, то луч, переходя в следующий слой, все больше отклоняется от вертикали ( 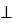 к границе раздела).
к границе раздела).
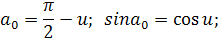
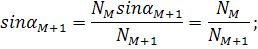
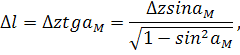
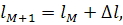
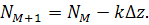
l=19*103м при 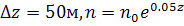
rem Реализация [2]
rem Так же и в среде VBA
Sub Мираж()
Pi=3.141596
for u=5 to 15 step 5
а= cos (u*Pi/180): h=1E-02: n=1.0004
x=0: z=0
m1: z=z+h
x =x +abs (h*a/sqr (1-a*a))
nl=n: n=n1+0.0004*exp (-0.05*z))
a1=a: a=a1*n1/n
if a<1 then goto m2
a=a1: h=-h
m2: if z>0 then goto m1
print u, x
next u
end sub
Справка: _________________________________
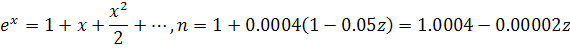
или
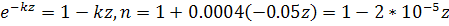
Задачи квантовой механики. Атом водорода. Ядро[2]
Поведение микрочастиц определяется волновой функцией ψ, которая определяется уравнением Шредингера:
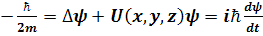 (2.1)
(2.1)
Если существуют стационарные решения, то есть такие состояния, в которых энергия имеет определенные, не зависящие от времени значения,
то правая часть (2.1) может быть записана в виде 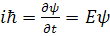 , где Е -собственные значения энергии.
, где Е -собственные значения энергии.
Если уравнение (2.1) рассматривать в одномерном случае, то оно примет вид:
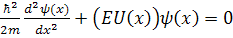 (2.2)
(2.2)
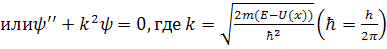 (2.3)
(2.3)
Если задан потенциальный рельеф, то есть функция U(x), то задача нахождения стационарных состояний сводится к нахождению таких функций ψ(x), которые удовлетворяют условию (2.3), то есть дифференциальному уравнению. При этом должны соблюдаться граничные условия: при переходе из области с одним значением U(x) к области с другим U(x) функция ψ(х) должна быть непрерывна вместе с её первой производной 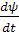 .
.
Очевидно, что это может быть выполнено только для определённых значений энергии Е - эти значения и соответствующие функции у/(х) называются собственными. Должно также выполняться условие
нормировки: 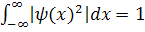 .
.
Длины волн линий излучения атома водорода определяются по формуле:
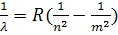 ,где постоянная Ридберга
,где постоянная Ридберга
R=1,097373-10-7м -1
n=1, 2, 3, ...
m=n+1, n+2, n+3, ...
Рассеяние а-частиц[2]
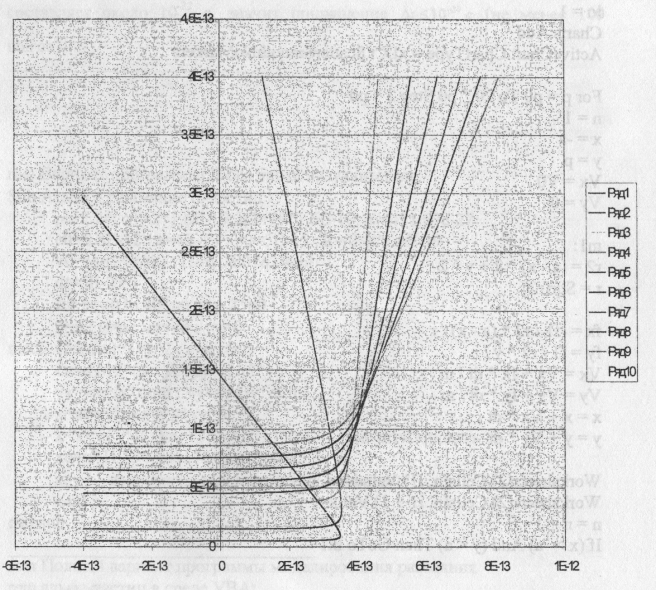
Задача: α-частицы с энергией 4 МэВ рассеиваются тонкой золотой фольгой. Нарисовать траектории частиц, приближающихся к ядру Аи. Прицельное расстояние р=2*10-15 м. На какие углы 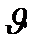 рассеиваются частицы и как зависит этот угол от прицельного расстояния p?
рассеиваются частицы и как зависит этот угол от прицельного расстояния p?
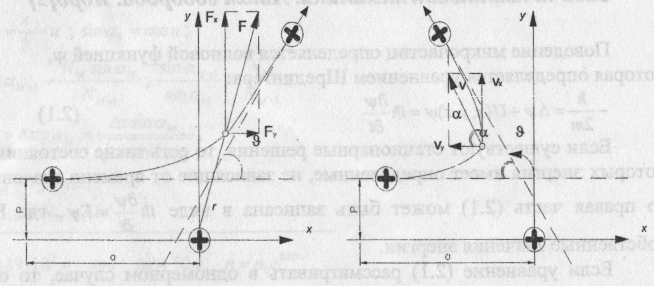
В основу решения уравнений движения берутся уравнения движения по осям x и у-в них входят составляющие силы Кулона. Если 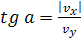 , то
, то
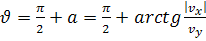 верно при больших |x| и |y|(по сравнению с расстоянием аи прицельным р).
верно при больших |x| и |y|(по сравнению с расстоянием аи прицельным р).
Сила Кулона 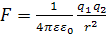 - сила отталкивания. Масса ядра Au (197 а.е.т.)>>массы а-частицы (4 а.е.т.=4*1,66*10-27кг),поэтому будем считать ядро неподвижным.
- сила отталкивания. Масса ядра Au (197 а.е.т.)>>массы а-частицы (4 а.е.т.=4*1,66*10-27кг),поэтому будем считать ядро неподвижным.
Из рисунка: 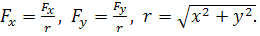
Уравнения движения по осям:
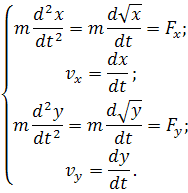
Начальные условия при t=0: x=-a; y=p; vy0=0.
Скорость vx находим из соотношения: 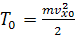 , где T0=4 МэВ →
, где T0=4 МэВ →
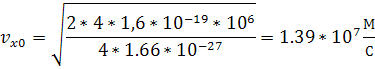
Соотношения для программирования:
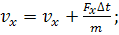
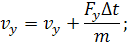
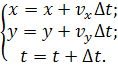
Расстояние а следует брать >> p (частица летит издалека, - а=10-11 м).
Далее, при скоростях порядка 107  - и расстояниях порядка 10-15 м время
- и расстояниях порядка 10-15 м время
составляет около 10-22 с, значит приращение 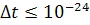 с (не менее 100 шагов).
с (не менее 100 шагов).
rem Вариант программы[2] без блока визуализации:
Sub Alpha()' рассеяние а-частиц
pi=3.14: q1=2*1.6E-19: q2=79*1.6E-19: m=4*1.67e-27
e0=8.8E-12 : a=4E-13 : p0=5E-15 : k=4E6*1.6E-19
v0=sqr(2*k/m): fl=ql/E0*q2/4/pi
dt=5E-23
for p=p0 to 40*p0 step 2*p0
x=0 : y=p : vx=v0 : vy=0
met2 :r2=(а-х)^2+у^2 : r=sqr(r2)
fx=-f1/r2*(a-x)/r : fy=f1/r2*y/r
vx=vx+fx*dt/m : vy=vy+fy*dt/m
x=x+vx*dt: y=y+vy*dt
x=x+vx"*dt : уе=170-у*1Е15*0.4 ' масштабировать
хе=х*1Е15 : ye=170-*1e15*0.4
x, у ' - запомнить для построения графика
next р
end sub
rem Полный вариант программы моделирования рассеяния
rem альфа-частиц в среде VBA:
Sub Z8()
n2 = 65
nЗ = 65
i1 = 1
pi = 3.14
ql = 2 * 1.6Е-19
q2 = 79* 1.6E-19
m = 4* 1.67E-27
E0 = 0.00000000000885
a = 0.0000000000004
p0 = 0.000000000000005
k = 4000000# * 1.6E-19
V0 = Sqr(2*k/m)
f1 = q1 / E0 * q2 / 4 / pi
dt = 5E-23
io = 1
Charts.Add
ActiveChart.ChartType = x1XYScatterSmoothNoMarkers
For p = p0 To 20 * p0 Step 2 * p0
n= 1
x = -a
y = p
Vx = V0
Vy = 0
m1:
r2 = (а-х)^2 + у^2
r = Sqr(r2)
fx = -f1 / r2 * (a - x) / r
fy = f1/r2*y/r
Vx = Vx + fx * dt / m
Vy = Vy + fy * dt / m
x = x + Vx * dt
у = у + Vy * dt
Worksheets(2).Cells(n, i1).Value = x
Worksheets(2).Cells(n, i1 + 1).Value = y
n = n+ 1
If (x > -a) And (y < a) Then GoTo ml
ActiveChart.SeriesCollection.NewSeries
If(io< 14) Then GoTo m2
ActiveChart.SeriesCollection(io).XValues = Worksheets(2).Range("A" +
Chr(n3) + "1 :A" + Chr(n3) + CStr(n))
ActiveChart.SeriesCollection(io).Values = Worksheets(2).Range("A" +
Chr(n3+ 1) + "1 :A" + Chr(n3 + 1) + CStr(n))
n3 = n3 + 2
GoTo m3
m2:
ActiveChart.SeriesCollection(io).XValues = Worksheets(2).Range(Chr(n2) + “1:" + Chr(n2) + CStr(n))
ActiveChart.SeriesCollection(io).Values = Worksheets(2).Range(Chr(n2 + 1) + "1:"+Chr(n2+ l) + CStr(n))
n2 = n2 + 2
m3:
io = io + 1
i1 =i1 +2
Next p
End Sub
Моделирование закономерностей теплового излучения[2]
Спектральная плотность излучения, т.е. энергия, излучаемая с площади 1 м2 за 1 с в пределах узкого интервала длин волн от λдо 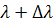 , отнесенная к этому интервалу dλ, равна
, отнесенная к этому интервалу dλ, равна
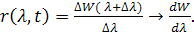
Согласно Планку:
ng w:val="EN-US" w:fareast="RU"/></w:rPr><m:t>rtО»</m:t></m:r></m:den></m:f></m:e></m:d><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:color w:val="000000"/><w:sz w:val="28"/><w:sz-cs w:val="28"/><w:lang w:val="EN-US" w:fareast="RU"/></w:rPr><m:t>-1</m:t></m:r></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 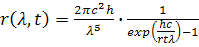
В системе СИ:
с = 3-10-8  , А = 6,62-10-34 Дж-с, k = 1,38-10-23
, А = 6,62-10-34 Дж-с, k = 1,38-10-23 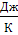
Закон Стефана-Больцмана для общей энергии теплового излучения с
единицы площади в единицу времени имеет вид:
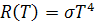 ,где
,где
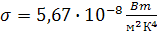 - постоянная Стефана-Больцмана.
- постоянная Стефана-Больцмана.
Закон Вина для длины волны, соответствующей максимуму излучения:
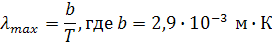
1. Построение кривой Планка.
Постройте график r(λ), если значение λ изменяется от 0 до 10 мкм при температуре 1000 К; 2000 К.
В системе СИ: 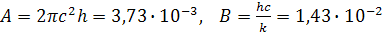
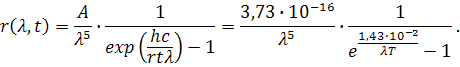
2. Закон Стефана-Больцмана.
Зная r(λ,t), определить энергию, излучаемую абсолютно черным телом с площади 1 м2 за 1 с, в видимом диапазоне (от λ=0,38 до 0,78 мкм) и в инфракрасном диапазоне (от λ=0,78 до ∞) при Т=1000 К; 2000 К. для проверки правильности работы программы найти также интегральную энергетическую светимость, т.е.
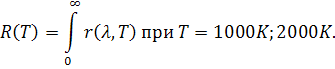
Определить, выполняется ли закон Стефана-Больцмана.
Задача сводится к вычислению определенного интеграла:
Получим:
 – в видимой области
– в видимой области
Всего во всем диапазоне длин волн:
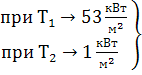 - вся энергия излучается в основном в инфракрасном диапазоне.
- вся энергия излучается в основном в инфракрасном диапазоне.
При вычислениях: 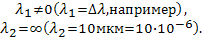
Видно, что R(2000)≈16∙R(1000), чтосоответствует закону Стефана-Больцмана.
Эту задачу легко реализовать в пакете MatLab:
Для вычисления интеграла 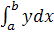 напишем m-сценарий (m-файл):
напишем m-сценарий (m-файл):
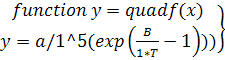 - файл quadf.m
- файл quadf.m
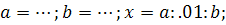
Шаг no x, у
>>quadf.m;
>>y=quadf(x);
>>plot (x,y);
>>Q=quad('quadf, a, b)
Экспериментальная проверка закона Стефана-Больцмана:
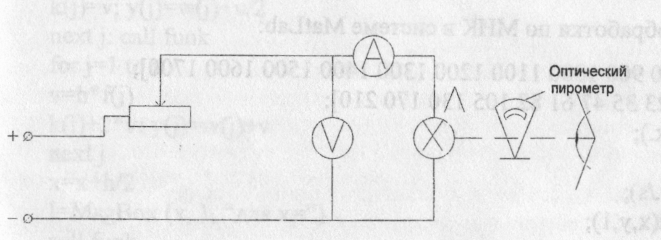
Потребляемая лампой накаливания мощность (следовательно, излучаемая мощность) P=RS (S - площадь) измеряется амперметром и вольтметром, а температура нити - оптическим пирометром. Излучающая площадь нити накаливания S=l см2. При различных значениях тока получаем значения температуры и мощности:
| t, °c | |||||||||||
| P, Вт |
Обработав данные по МНК, найти 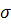 и n.
и n. 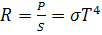 . Применим
. Применим
функциональный масштаб: 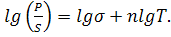 Пусть
Пусть
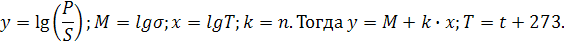
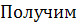
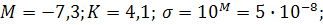
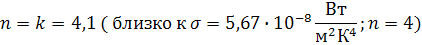
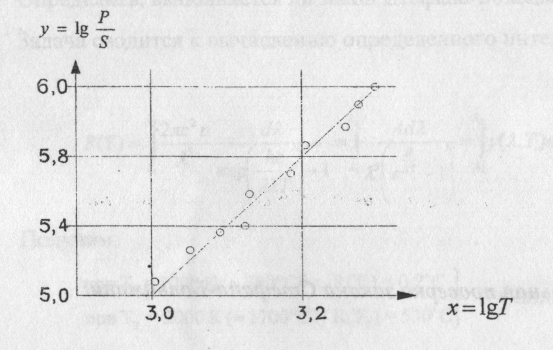
Программа обработки по МНК в системе MatLab:
>>х=[700 800 900 1000 1100 1200 1300 1400 1500 1600 1700];
>>у=[11 17 23 35 47 61 82 105 130 170 210];
>>x=log10(x.);
>>s=0.0001;
>>y=log10(y./s);
>>p1=polyfit(x,y,1);
>>stem(x,y);
>>hold
>>x1=xn:h:xk; % - задать x - начальное, шаг, x -конечное
>>y1 =polyval(p1 ,x1);
>>plot(x1,y1);
>>grid,set(gca,'FontName','Arial Cyr','FontSize', 16),
>>title('Закон Стефана-Больцмана');
>>xlabel('Аргумент, lgT');
>>уlabel ('Функция, lg(P/S)');
Дата добавления: 2016-02-04; просмотров: 1167;
