Вычисление неопределенности измерения

1) вычисление неопределенности по типу А:

– стандартные неопределенности входных величин

;

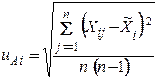– суммарная стандартная неопределенность по типу А:

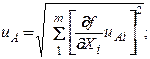
2) вычисление неопределенности по типу В:

– стандартная неопределенность каждой входной величины

,

b – границы отклонения измеряемой величины;

k = 1,1 при доверительной вероятности Р_д = 0,95;

– суммарная стандартная неопределенность по типу В:

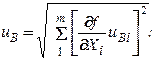
3) вычисление суммарной стандартной неопределенности

;

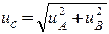4) вычисление расширенной неопределенности

U_P = k u_c ,

k = t_P(v_е) ; .

5) форма представления результата измерения:

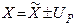, u_c , k , v_е .

6) интерпретация полученных результатов: интервал ( 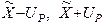) содержит долю, равную Р_д, распределения значений, которые могли бы быть обоснованно приписаны измеряемой величине.

Измерительный эксперимент

Цель – установление вида функциональной зависимости (математической модели) исследуемой величины: Y = f (Х₁, … Х_m).

При изменении одного фактора и фиксированных уровнях других – однофакторный эксперимент (Х – фактор; Y – отклик).