Загальний випадок — т ≠р
У цьому випадку для нарощеної суми маємо:
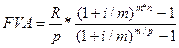(5.14)
Знаючи нарощену величину такої ренти, можна знайти її теперішню вартість з наступного рівняння :
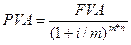(5.15)
Розглянемо окремі випадки цієї ренти.
2. Річна рента (р = 1) з нарахуванням відсотків т- разів за рік.
Якщо відсотки нараховують т - разів на рік, а платежі є річними, то нарощена сума дорівнює:
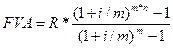(5.16)
Теперішню величину такої ренти обчислюють за формулою (5.15).
3. р - термінова рента з нарахуванням відсотків один раз за рік (т = 1)
Якщо платежі здійснюються декілька разів за рік, а відсотки нараховують один раз на рік нарощена сума дорівнює:
(5.17)
Теперішню величину такої ренти розраховують за формулою (5.4).
4. р — термінова рента з т =р
Досить часто у фінансових обчисленнях припускають, що кількість платежів за рік та кількість нарахувань відсотків збігаються (тобто т=р).
Майбутня сума такої ренти дорівнює:
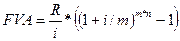(5.18)
Теперішню величину цієї ренти обчислюють за формулою (5.16).
Найскладнішими в математичному плані є фінансові ренти, що описують неперервним змінним потоком платежів. На сьогодні, вони майже незастосовні на практиці, проте є окремим напрямом наукових досліджень.
У фінансових обчисленнях, які стосуються таких потоків платежів, вважають, що коли потік неперервний, то розміри платежів у часі описуються функцією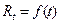 
, а для нарахування відсотків використовують процентну ставку у вигляді сили росту .
Необхідно зазначити, що оскільки за допомогою потоків платежів здійснюються майже всі фінансові розрахунки в економіці, то різноманітність схем та механізмів фінансових операцій зумовлює існування і інших (крім розглянутих вище) видів фінансових рент.
Дата добавления: 2016-02-02; просмотров: 484;