Гидродинамическая теория детонационной волны

На рис. №1.16 приведена ударная адиабата вещества, начальное состояние которого 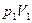.При ударном сжатии состояние этого вещества скачком изменилось до 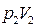.Уравнение прямой 2 , связывающее давление, удельные объёмы и скорость детонации, в соответствии с выведенным из закона сохранения количества движения уравнением, имеет вид

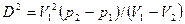
Чем круче прямая 2, тем больше скорость детонации.

Преобразуем представленное уравнение к виду

Р₂ = Р₁ + 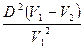. (1.29)

Это уравнение описывает прямую Михельсона, которая является касательной в точке М к адиабате продуктов взрыва ( кривая 3). Точка М называется точкой Жуге. В этой точке завершается реакция в детонационной волне и завершается выделение тепла в ходе этой реакции.

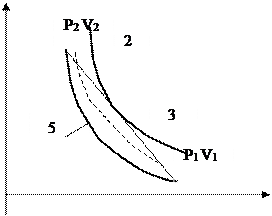Р

В

V

Рис. №1.16 Ударная адиабата вещества (кривая 5). Прямая 2 , описываемая приведённым уравнением, на же прямая Михельсона.3–Ударная адиабата продуктов взрыва. Точка М - точка Жуге.

Участок ВМ соответствует промежуточным адиабатам, характерным для не завершившихся реакций. Давление в точке Жуге будет приблизительно в 2 раза меньшим давления на фронте детонационной волны, поскольку продукты детонации успевают расшириться. Участок от момента ударного сжатия(точка В) до завершения реакции называется химическим пиком.

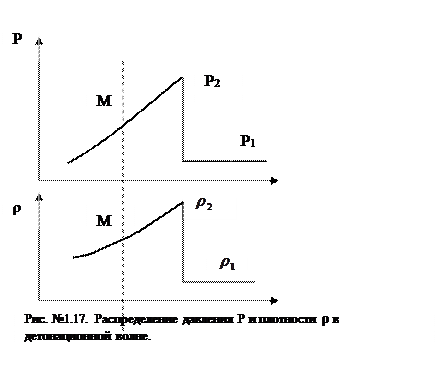
На рис. № 1.15 показано распределение давления и плотности в

детонационной волне, в том числе в точке Жуге (М).

Адиабата продуктов взрыва смещена в результате выделения тепла при химической реакции. Точка М лежит на адиабате Гюгонио для конечных продуктов детонации и является особой точкой, в которой энтропия постоянна, а скорость детонации равна сумме скоростей движения продуктов взрыва - u и местной скорости звука в продуктах взрыва – с , D = u + c.

1.3.4 Отражение от абсолютно жёсткой стенки слабых ударных волн. Акустический парадокс.

Задачи распространения слабых ударных волн в средах решаются в предположении постоянства энтропии. Такой подход к постановке задачи называется методом акустического приближения. Одним из главных допущений этого метода является констатация постоянства скорости распространения возмущений. Рассмотрим случай отражения слабой ударной волны от абсолютно жёсткой стенки. В определённый момент времени плоская ударная волна, распространяющаяся со скоростью D, падает на жёсткую стенку в точке О. При этом фронт волны составляет с жёсткой стенкой угол α. За фронтом волны среда приобретает скорость v. Нормальная составляющая этой скорости к жёсткой стенке равна v cos α . На самой жёсткой стенке нормальная составляющая скорости должна быть равна нулю. Это может реализоваться только в том случае, когда в точке О возникнет ещё один фронт волны такой интенсивности и направленный таким образом , что он вызовет движение среды за фронтом с такой же величиной нормальной составляющей скорости, но направленной строго противоположно v cos α. Применительно к изображённой на рисунке 16 схеме будет выполняться равенство v cos α = v^* cos α*

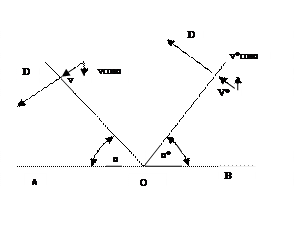
В случае малых возмущений как прямая , так и отражённая волна будут распространяться с одинаковой скоростью D, равной скорости звука. Тогда скорость перемещения точки О вдоль луча ОА должна быть равна D/sin α , а вдоль луча ОВ- D/sin α^* или D/sin α = D/sin α^*.

Из этого равенства следует известный закон акустического отражения: α = α^*. В свою очередь из этого равенства следует равенство массовых скоростей v = v^*. А поскольку давление на фронте ударной волны равно Р = ρDv , то в силу равенства v и v^* давление на жёсткой стенке независимо от угла падения прямой волны будет равно 2 ρDv или удвоенному давлению на фронте падающей ударной волны. В этом и состоит так называемый акустический парадокс. При значении угла α, равном 90 ⁰ отражение волны не происходит, волна скользит вдоль стенки и давление на стенке равно Р = ρDv.