Гидродинамическая теория плоской ударной волны

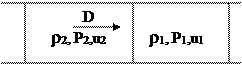
Простая схема для вывода уравнений гидродинамической теории ударной волны представлена на рис. №1.14. Рассмотрим цилиндрическую трубу с площадью внутреннего сечения S и заполненную газом. По газу слева направо распространяется ударная волна со скоростью D относительно неподвижных стенок трубы. Фронт волны совпадает с сечением АВ. Невозмущённое состояние среды справа от сечения АВ характеризуется следующими параметрами: ρ₁, P₁,u_1. За фронтом волны среда мгновенно приобретёт параметры: ρ₂, P₂,u₂. Скорости u_{2 ,}u₁ направлены направо. Относительно системы координат, движущейся

со скоростью u_{1 ,}скорость фронта УВ равна D – u₁, а скорость потока среды за фронтом будет соответствовать u₂ - u_1.

Для того чтобы граница между возмущённым и невозмущённым состоянием среды оставалась неподвижной необходимо рассмотреть систему координат, которая движется с постоянной скоростью D, то есть она привязана к скачку параметров среды. В такой системе координат невозмущённая среда будет двигаться справа налево со скоростью -D + u₁ , а возмущённая среда - справа налево со скоростью –D+ u_{2 .}

Через промежуток времени τмасса газа в невозмущённой среде, прошедшая через границу АВ будет равна (- D + u₁ )τS ρ₁. Эта же масса за фронтом УВ в возмущённой среде может быть выражена как (-D+ u₂)τS ρ₂ . Из закона сохранения массы следует

(- D + u₁ )τS ρ₁ = ( -D + u₂)τS ρ₂. или

( D – u₁ )ρ₁ = (D- u₂)ρ₂. (1.11)

Для получения связи между разностью давлений в возмущённой и невозмущённой зонах и скоростями движения газа в этих зонах применим второй закон Ньютона

F τ = M (v₂ - v₁), (1.12)

где F – сила , τ - время действия силы, M - масса невозмущённого газа, подверженная действию силы.

Для рассматриваемого случая сила направлена справа налево и поэтому в выбранной системе координат

F = -(Р₂ – Р₁) S. (1.13)

а масса в этой же системе координат М = ( -D + u₁ )τS ρ₁ или с учётом того, что

(v₂ - v₁) =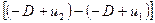

-(Р₂ – Р₁) S τ = -( D - u₁ )τS ρ₁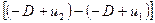

После упрощения получим следующее соотношение

(Р₂ – Р₁) = ρ₁ ( D – u₁ )· (u₂ - u₁). (1.14)

При Р₁ = 0 и u₁ =0 получаем фундаментальное соотношение для скачка давления на фронте волны

=

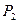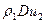
Теперь получим соотношение между изменением энергии и изменением плотности или удельного объёма при переходе системы из невозмущённого в возмущённое состояние. Для этого запишем уравнение сохранения энергии. Обозначим внутреннюю энергию единицы массы среды Е. Кинетическую энергию единицы массы - u² /2.

При перемещении разрыва затрачивается работа, равная .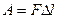

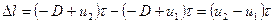
Тогда в соответствии с (1.13) получим

(1.15)

Отнеся эту работу к полной массе среды, участвующей в движении, и проведя сокращение числителя и знаменателя на Sτ получим величину работы на единицу массы среды.

Работа сил давления затрачивается на увеличение кинетической энергии единицы массы

среды и её внутренней энергии, т.е.

(Р₂ u₂ - Р₁ u₁ ) / ( D - u₁ ) ρ₁ =( E₂ - E₁ ) + (u₂²/2 - u₁²/2) (1.16)

Заменяя в (1.11) плотность на удельный объём ρ = 1/v получим

( D – u₁ ) / v₁ = (D – u₂ ) /v₂ .

Умножив обе части уравнения на v₁ v₂ получим следующий вид уравнения

( D – u₁ ) v₂ = (D – u₂ ) v₁ или

D = ( u₁ v₂ - u₂ v₁ ) / ( v₂ - v₁)

Вычтем из левой и правой части u₁ и после преобразования будем иметь

D – u₁=v₁ (u₂ - u₁) / v₁ - v₂ или( D – u₁)/v₁ = (u₂ - u₁) /( v₁ - v₂ ) (1.17)

C другой стороны из (1.13) после замены плотности на удельный объём получим

( D – u₁) / v₁ = (Р₂ – Р₁)/ (u₂ - u₁) (1.18)

Сравнивая (1.17) и (1.18) получим

(Р₂ – Р₁)/ (u₂ - u₁)=(u₂ - u₁) / v₁ - v₂ или (u₂ - u₁)² = (Р₂ – Р₁) . (v₁ - v₂ )

Тогда u₂-u₁=[(Р₂–Р₁).(v₁-v₂)]^0,5.(1.19)

Из (1.17) следует (u₂-u₁)=(D–u₁)(v₁-v₂)/v₁ (1.20)

Приравнивая правые части уравнений (1.19) и (1.20) получаем выражение для определения скорости ударной волны

D – u₁ = v₁ [(Р₂ – Р₁) / ( v₁ - v₂ ) ] ^{0, 5} (1.21)

Используем уравнения (1.17) и (1.21) для преобразования уравнения баланса энергии

Из уравнения баланса энергии изменение внутренней энергии единицы массы среды будет соответствовать (см.1.16)

E₂-E₁=(Р₂ u₂ - Р₁ u₁ ) / (D-u₁ ) ρ₁-(u₂²/2- u₁²/2) (1.22)

(D-u₁ ) ρ₁ заменим в соответствии с (1.18) на (Р₂ – Р₁)/ (u₂ - u₁) и получим

E₂-E₁=(Р₂u₂ - Р₁ u₁ ) (u₂ - u₁)/ (Р₂ – Р₁) - (u₂²/2- u₁²/2).

Последнее уравнение преобразуем к виду

E₂ - E₁=0,5(u₂ - u₁) [ 2 (Р₂ u₂ -Р₁ u₁ ) / (Р₂ – Р₁)-(u₂ + u₁)]. (1.23)

Выражение в квадратных скобках после элементарных преобразований примет следующий вид

(Р₂ +Р₁) (u₂ - u₁) / (Р₂ – Р₁)

Подставим в (1.22) и получим

E₂ - E₁ = 0,5(u₂ - u₁)² (Р₂ +Р₁) / (Р₂ – Р₁) или окончательно

E₂ -E₁ = 0,5 (Р₂ +Р₁) ( v ₁ - v₂ ) (1.24)

Это и есть уравнение Гюгонио.

Для идеального газа и в общем случае среды, подчиняющейся политропическому закону РV^k = const, имеем E = P v / k -1.

Где k=Cp/Cv-отношение теплоёмкостей при постоянном давлении и постоянном объёме.

Е₁=P₁v₁/k₁-1 и Е₂ = P₂ v₂ / k₂ -1 (1.25)

Выведем уравнение ударной адиабаты . Для этого в уравнение Гюгонио

(1.24) подставим значения внутренней энергии из (1.25)

P₂ v₂ / k₂ -1-P₁ v₁/k₁ -1= 0,5 (Р₂ +Р₁) ( v ₁ - v₂ ) (1.26)

Для не очень сильных ударных волн можно принять с небольшой погрешностью k_{1 =} k_{2 =} k

Тогда (1.25) можно записать в виде

P₂ v₂ / k -1 - P₁ v₁ / k -1 = 0,5 (Р₂ +Р₁) ( v ₁ - v₂ )

Проведя элементарные преобразования получим

P₂/P₁=[(k+1)ρ₂–(k-1)ρ₁]/[(k+1)ρ₁–(k-1)ρ₂] и (1.27)

ρ_{2 /} ρ₁=v_1/ v₂=[(k +1)P₂+(k-1)P₁]/[(k+1)P₁+(k-1) P₂ ] (1.28)

Уравнения (1.27) и (1.28) носят название ударной адиабаты или адиабаты Гюгонио.

Эта адиабата отражая закон сохранения энергии, является аналогом обычной адиабаты и справедлива для ударных волн, распространяющихся в политропных средах.

На рис.№1.15 представлены адиабаты Пуассона (1) и Гюгонио(2).

Как следует из рисунка, адиабата Гюгонио имеет более крутой подъём по оси ординат.

Представим (1.28) в виде

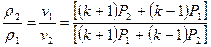
При неограниченном возрастании скачка давления(P₂ /P₁→∞) отношение плотностей газа после и до скачка стремится к конечному пределу , равному k +1 / k -1. Этот результат является следствием необратимости процесса адиабатного сжатия газа ударной волной, сопровождающегося диссипацией энергии и возрастанием энтропии.

Выведенные нами соотношения для ударных волн могут быть представлены в виде системы уравнений :

u₂ - u₁ = [(Р₂ – Р₁) . (v₁ - v₂ )] ^0,5 .

D – u₁ = v₁ [(Р₂ – Р₁) / ( v₁ - v₂ ) ] ^{0, 5} (1.29)

E₂ - E₁ = 0,5 (Р₂ +Р₁) ( v ₁ - v₂ )

Р = f(ρ, E )

В этой системе 4 –х уравнений имеется 5 основных неизвестных:

Р₂ , u₂ , v₂ , D , E₂ .

Задаваясь одним каким – либо параметром УВ имеется возможность найти все остальные.