ОЦЕНКА СОГЛАСОВАННОСТИ СУЖДЕНИЙ ЭКСПЕРТОВ

При оценке объектов исследования эксперты зачастую расходятся во мнениях по решаемой проблеме. В связи с этим возникает необходимость количественной оценки степени согласия экспертов. Получение количественной меры согласованности позволяет более обоснованно интерпретировать причины расхождения мнений.

Оценка согласованности суждения экспертов основывается на использовании понятия компактности, наглядное представление о котором дает геометрическая интерпретация результатов экспертизы. Оценка каждого эксперта представляется как точка в некотором пространстве, в котором имеется понятие расстояния. Если точки, характеризующие оценки всех экспертов, расположены на небольшом расстоянии друг от друга, т.е. образуют компактную группу, то, очевидно, можно это интерпретировать как хорошую согласованность мнений экспертов. Если же точки в пространстве разбросаны на большие расстояния, т.е. не принадлежат одной области, то согласованность мнений экспертов невысокая. Возможно, что точки - мнения экспертов - расположены в пространстве так, что образуют две или несколько компактных групп. Это означает, что в экспертной группе существуют две или несколько существенно отличающихся точек зрения на оценку объектов исследования. Может быть область точек, не образующих совокупности мнений - размытая область. В этом случае не удалось обнаружить точек зрения на решаемую проблему. Лицо, принимающее решение, может повторить экспертизу или принять какое-либо решение самостоятельно.

Конкретизация изложенной идеи оценки согласованности мнений экспертов производится в зависимости от использования количественных или качественных шкал измерения и выбора меры степени согласованности.

При использовании количественных шкал измерения и оценке всего одного объекта все мнения экспертов можно представить как точки на числовой оси. Эти точки можно рассматривать как реализации случайной величины и поэтому для оценки центра группировки и разброса точек представляется возможным использовать хорошо разработанные методы математической статистики. Центр группировки точек можно определить как математическое ожидание (среднее значение) или медиану случайной величины, разброс количественно оценивается дисперсией случайной величины. Мерой согласованности оценок экспертов, т.е. компактности расположения точек на числовой оси, может служить отношение среднеквадратического отклонения к математическому ожиданию случайной величины.

Если объект оценивается несколькими числовыми параметрами, то мнение каждого эксперта представляется как точка в пространстве параметров. Центр группировки точек опять вычисляется как математическое ожидание вектора параметров, а разброс точек - дисперсией вектора параметров. Мерой согласованности суждений экспертов может служить в этом случае сумма расстояний оценок от среднего значения, отнесенная к расстоянию математического ожидания от начала координат. Мерой согласованности может служить количество точек, расположенных в радиусе среднеквадратического отклонения от математического ожидания, ко всему количеству точек. Различные методы определения согласованности количественных оценок на основе понятия компактности (близости) рассматриваются в теории группировок и распознавания образов.

При измерении объектов в порядковой шкале согласованность оценок экспертов в виде ранжировок или парных сравнений объектов также основывается на понятии компактности.

Метод простого ранжирования заключается в том, что каждый эксперт располагает признаки в порядке предпочтения. Цифрой 1 обозначается наиболее важный признак, цифрой 2 - следующий по важности и т. д. Полученные результаты сводятся в таблицу, общий вид которой представлен в таблице 8.6.1.

Таблица 8.6.1

Сводная таблица результатов

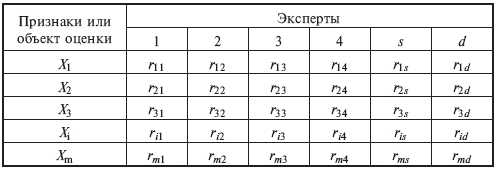
После того, как данные от экспертов собраны, проводится обработка полученных оценок.

При ранжировании объектов используется мера согласованности мнений группы экспертов - дисперсионный коэффициент конкордации (коэффициент согласия).

Рассмотрим матрицу (табл.8.6.1) результатов ранжировки m объектов группой из d экспертов

||r_is|| ,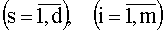

где r_is - ранг, присваиваемый s-экспертом i-му объекту. Составим суммы рангов по каждой строке. В результате получим вектор с компонентами

.

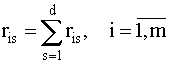Будем рассматривать величины r_i как реализации случайной величины и найдем оценку дисперсии. Как известно, оптимальная по критерию минимума среднего квадрата ошибки оценка дисперсии определяется формулой:

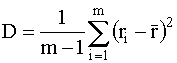, (8.1)

где 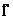- оценка математического ожидания (средний ранг), равная

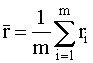. (8.2)

Дисперсионный коэффициент конкордации определяется как отношение оценки дисперсии (8.1) к максимальному значению этой оценки:

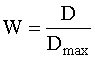. (8.3)

Коэффициент конкордации изменяется от нуля до единицы, поскольку 0£D£D_max.

Максимальное значение дисперсии равно

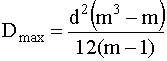. (8.4)

Введем обозначение

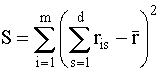. (8.5)

Используя (8.5), запишем оценку дисперсии (8.1) в виде

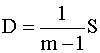. (8.6)

Подставляя (8.4), (8.6) в (8.3) и сокращая на множитель (m-1), запишем окончательное выражение для коэффициента конкордации

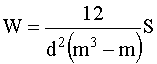. (8.7)

Данная формула определяет коэффициент конкордации для случая отсутствия связных рангов. При W=0 согласованность оценок различных экспертов отсутствует, а при W=1 согласованность мнений экспертов полная.

При крайних коэффициентах конкордации могут быть даны следующие рекомендации. Если W=0, то для получения достоверных оценок следует уточнить исходные данные о событиях и (либо) изменить состав группы экспертов. При W=1 не всегда можно считать оценки объективными, поскольку может оказаться, что все члены экспертной группы условились придерживаться одинаковых взглядов.

Необходимо, чтобы найденное значение W было больше заданного значения W_З (W>W_З). Обычно принимается W=0,5, т.е. при W>0,5 выводы экспертов согласованы в большей мере (сходятся в оценке событий), чем несогласованы. При W<0,5 оценки нельзя считать в достаточной степени согласованными.

При наличии связных рангов коэффициент конкордации вычисляется по формуле

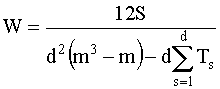, (8.8)

где

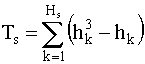, (8.9)

В формуле (8.9) T_s - показатель связных рангов в s-й ранжировке, H_s - число групп равных рангов в s-й ранжировке, h_k - число равных рангов в k-й группе связных рангов при ранжировке s-м экспертом. Если совпадающих рангов нет, то H_s=0, h_k=0 и, следовательно, T_s=0. В этом случае формула (9.8) совпадает с формулой (8.7).

Коэффициент конкордации представляет собой случайную величину. Оценка значимости W может быть произведена по критерию Пирсона χ². Величина d(m-1)W имеет χ² = распределение с χ = m-1 степенями свободы.

При наличии связных рангов χ² = распределение с ν = m-1 cтепенями свободы имеет величину

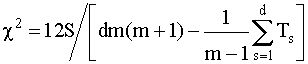. (8.10)

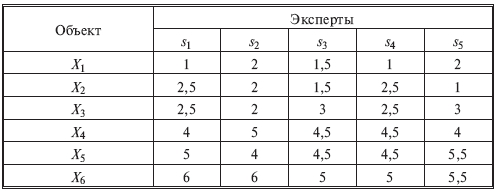
ПРИМЕР 1. Результаты ранжировки шести объектов (X₁, X₂, X₃, X₄, X₅ и X₆) пятью экспертами (s₁, s₂, s₃, s₄, s₅) представлены в табл.8.6.2

Таблица 8.6.2

Сводная таблица результатов ранжирования

Вычислим коэффициент конкордации и произведем оценку его значимости. Среднее значение 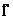по формуле (8.2) равно

.

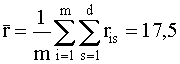Величина S в соответствии с формулой (8.5) равна

.

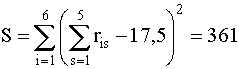Поскольку в ранжировке имеются связные ранги, то вычисление коэффициента конкордации выполняется по формуле (8.8). Предварительно вычисляются T_s, используя формулу (8.9). В данном примере из табл. 8.6.2 следует, что в ранжировке экспертом s₁ имеется одна группа связных рангов, поэтому Н₁=1, а в этой группе содержится два связных ранга, равных 2,5, поэтому k=1 и h₁=2. Отсюда Т₁=2³-2=6. Аналогичным образом вычисляются Т₂...Т₅:

Ò₂=3³-3=24; Ò₃=2³-2+2³-2=12; Ò₄=2³-2+2³-2=12; Ò₅=2³-2=6.

Подставляя значения Т_s, S и m=6, d=5 в формулу (8.8) и произведя вычисления, получаем

W = 12´361 / [5²(6³-6)-5´60] = 0,874.

Оценим значимость коэффициента конкордации. В данном случае число степеней свободы ν=m-1=6-1=5. Табличное значение 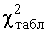для ν=5 и 5% уровня значимости равно 11,07 (табл. 8.6.2). Вычисляя значение χ² по формуле (8.10), получаем

χ² = 12´361 / [5´6´7 - 0,25´60] = 21,8.

Поскольку 11,07<21,8, то гипотеза о согласии экспертов в ранжировках принимается.