Реализация операции умножения двоичных чисел
ai • bi , если ai • bi < g;
Si умн =
ai • bi – ( ](ai • bi)/g[ -1) , если ai • bi ³ g.
 | |
 |
0, если ai • bi < g;
ri умн =
](ai • bi)/g[ -1, если ai • bi ³ g.
Подобно алгоритму сложения можно привести правило умножения двух цифр ai и bi i-го разряда при произвольном основании системы счисления
Обозначение: ]*[ — целая часть представленной в скобках дроби.
При g = 2 система, представляющая алгоритм, упрощается, так как ri всегда равно нолю, а Si умн равно логическому произведению ai и bi. При перемножении чисел операции над знаками и численными значениями производятся раздельно, при нашей кодировке при определении знака произведения можно использовать функцию неэквивалентности; необходимое для размещения произведения число разрядов при n-разрядных сомножителях равно 2•N. Образование произведения сводится к суммированию частных произведений с учетом сдвига разрядов; для n-разрядных сомножителей необходимо сложить (n–1) пару слагаемых, именно такой алгоритм реализуется в большинстве устройств вычислительной техники, однако скорость выполнения операции умножения в соответствии с этим алгоритмом не достаточно высока для применения при обработке сигналов в режиме реального времени.
Метод ускоренного умножения может быть реализован в матричных вычислительных устройствах. Метод ускоренного умножения сводится к одновременному образованию всех частных произведений и их суммированию на полных одноразрядных сумматорах.
| A | B |
| a0 a1 a2 | b0 b1 b2 |
a2 a1 a0
b2 b1 b0
a2b0 a1b0 a0b0
a2b1 a1b1 a0b1
a2b2 a1b2 a0b2 .
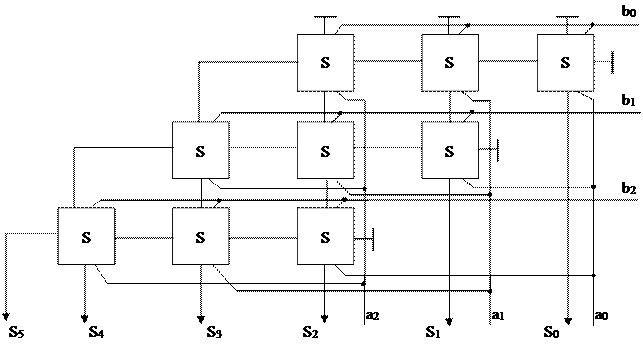 S5 S4 S3 S2 S1 S0
S5 S4 S3 S2 S1 S0
Рис. 1.6.3Схема перемножителя двух двоичных 3-хразрядных чисел на полных одноразрядных сумматорах
В основе такого устройства, как видно, лежит полный одноразрядный сумматор, выполненный в виде комбинационного устройства — матричного перемножителя, схема которого приведена на рис. 1.6.4.
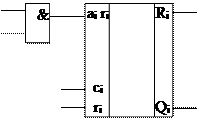 |
Рис. 1.6.4Схема электрическая принципиальная матричного перемножителя
Таблица состояний матричного перемножителя выглядит следующим образом:
| ai | bi | ri | ci | Ri | Qi |
Дата добавления: 2016-02-02; просмотров: 691;
