Соединение треугольником

Трёхфазная цепь при соединении источника и приёмника треугольником имеет разветвлённую многоконтурную схему (рис. 5.9).

Расчёт этой сложной цепи значительно упрощается, если не принимать во внимание сопротивление проводов.

В этом случае напряжения на фазах приёмника равны соответствующим напряжениям источника и, как правило, представляют собой симметричную систему.

Если трёхфазная система напряжений, приложенных к приёмнику, известна, то фазные токи в симметричном приёмнике определяются порознь по известным формулам:

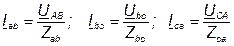. (5.17)

Токи в линейных проводах:

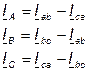. (5.18)

Если же сопротивления линейных проводов необходимо учитывать, то для расчёта цепи следует преобразовать треугольник сопротивления нагрузки в звезду, определить токи в линейных проводах с учётом формулы (5.13) и затем найти напряжения и токи фаз нагрузки.

При симметричной нагрузке фаз достаточно провести расчёт одной фазы.

5.4 Измерение мощности в трёхфазных цепях

Активной мощностью трехфазной системы назы­вают сумму активных мощностей ее отдельных фаз:

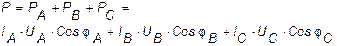. (5.19)

При симметричной нагрузке мощности отдельных фаз равны между собой, а общая мощность опреде­ляется как

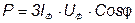. (5.20)

На практике мощность трехфазной системы чаще выражают через линейные, а не через фазные токи и напряжения.

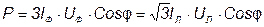. (5.21)

Для трехфазной системы также справедливы сле­дующие соотношения для полной, активной и реак­тивной мощностей, соответственно:

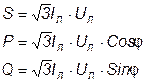. (5.22)

Существуют несколько методов измерения мощ­ности трехфазной системы, у каждого из них своя область применения.

1.Способ одного ваттметра.

2.
Используют для измерения мощности при симметричной нагруз­ке, соединенной звездой с доступной нулевой точ­кой (рис. 5.13).

В этом случае общая мощность трехфазной систе­мы равна утроенному показанию ваттметра:

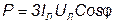. (5.23)

3.Способ трех ваттметров

Применяют для измерения мощности при неравномерной нагрузке, соединенной звездой. В каждый из линейных про­водов включается токовая цепь одного из ваттмет­ров, а их цепи напряжения включаются между соответствующим линейным проводом и нулевым про­водом системы (рис. 5.14).

Активная мощность всей трёхфазной системы равна сумме показаний ваттметров:

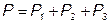. (5.24)

3.Способ двух ваттметров.

Этот способ уни­версален - он применяется при симметричной и не­симметричной нагрузках и при любом типе соеди­нения. Нулевой провод может быть, а может и от­сутствовать - он просто не используется. Токовые обмотки ваттметров включают в какие-нибудь две фазы, а обмотки напряжения между третьей (неза­нятой) фазой и той фазой, в которую включена токовая обмотка данного ваттметра (рис. 5.15).

В этом случае общая мощность трехфазной сис­темы равна алгебраической сумме показаний двух ваттметров.

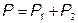. (5.25)

5.5 Аварийные режимы

Аварийные режимы (обрыв, короткое замыкание) крайне нежелательны на практике, так как могут привести к поломке оборудования. Рассмотрим некоторые случаи аварийных режимов.

Трёхпроводная система:

1. Звезда без нулевого провода

а) обрыв одной из фаз нагрузки, например фазы а ( 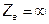) (рис. 5.16)

В этом случае сопротивления фаз b и с включены последовательно, а токи в линейных проводах В и С

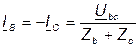. (5.26)

Напряжения фаз нагрузки становятся равными

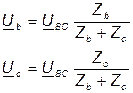. (5.27)

Эту же электрическую цепь можно считать трёхфазной и вести расчёт, пользуясь формулой смещения (при этом 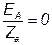, так как ).

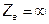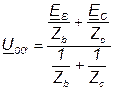. (5.28)

Если Z_b = Z_c, то

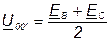; (5.29)

б) При коротком замыкании фазы нагрузки, например фазы а, ( 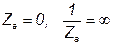). Напряжение смещения нейтрали:

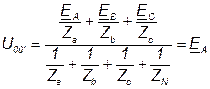. (5.30)

Следовательно фазы нагрузки b и c находятся под соответствующими линейными напряжениями.

2. Соединение треугольником:

а) при обрыве одной из фаз нагрузки, например фазы AB (рис 5.17).

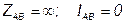
Для упрощения примем, что Z_AB = Z_CA = R, тогда

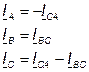(5.31)

Независимо от режима AB напряжение на фазах нагрузки Z_BC и Z_CA остаётся неизменным.

б) при обрыве линейного провода, например провода А (рис. 5.17), схема преобразуется в однофазную. Для упрощения примем Z_AB = Z_BC = Z_CA = R, тогда

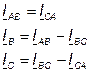(5.32)

Напряжение на фазах нагрузки AB и CA уменьшатся в два раза.

Для общего случая:

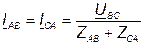; (5.33)

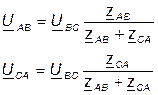(5. 34)