Понятие логической функции
Чем занимается математическая логика? Логика как искусство рассуждении зародилась в глубокой древности. Начало науки о законах и формах мышления связывают с именем Аристотеля. Прошло два тысячелетия, прежде чем Лейбниц предложил ввести в логику математическую символику и использовать ее для общих логических построений. Эту идею последовательно реализовал в прошлом столетии Джордж Буль и тем самым заложил основы математической (символической) логики.
Главная цель применения в логике математической символики заключалась в том, чтобы свести операции с логическими заключениями к формальным действиям над символами. При этом исходные положения записываются формулами, которые преобразуются по определенным законам, а полученные результаты истолковываются в соответствующих понятиях.
Бурное развитие математической логики связано, прежде всего, с задачами обоснования математики, где она используется для доказательства непротиворечивости исходных понятий и правильности рассуждении и выводов математических теорий. Некоторые ученые даже склонны рассматривать логику как одну из наиболее общих наук, частью которой является сама математика.
В последние десятилетия логика находит все более широкое применение в технике при исследовании и разработке релейно-контактных схем, вычислительных машин, дискретных автоматов. Ее методы используются в теории преобразования и передачи информации, теории вероятностей и комбинаторном анализе. Математическая логика начинает внедряться в такие нематематические области, как экономика, биология, медицина, психология, языкознание, право. Интенсивно развиваются специальные разделы математической логики, призванные обслуживать конкретные области науки и техники.
Столь энергичный выход математической логики за пределы математики объясняется тем, что ее аппарат легко распространяется на объекты самой общей природы, лишь бы только они характеризовались конечным числом состояний.
Двузначная логика имеет дело с такими объектами, которые принимают одно из двух возможных значений (истинное или ложное высказывание, высокое или низкое напряжение, наличие или отсутствие заданного признака у объекта и т. п.). Объекты, которые могут принимать значения из конечного множества, содержащего больше двух элементов, называют многозначными. Они либо сводятся каким-нибудь способом к двузначным объектам, либо обслуживаются аппаратом многозначной логики.
Устоявшееся представление о математической логике как науке, изучающей законы мышления с применением аппарата математики, главным образом, для нужд самой математики, в современных условиях становится слишком узким. С расширением областей применения и дальнейшим развитием математической логики изменяется и взгляд на нее. Объектами математической логики являются любые дискретные конечные системы, а ее главная задача – структурное моделирование таких систем.
Булевы функции. Объекты с двумя возможными состояниями характеризуются булевыми переменными, которые способны принимать лишь два различных значения. Для обозначения этих двух значений обычно используются цифры 0 и 1 или буквы Л (ложно)
и И (истинно).
Отношения между булевыми переменными представляются булевыми функциями, которые подобно числовым функциям могут зависеть от одной, двух и, вообще, n переменных (аргументов). Запись у = f(x1, x2, …,xN) означает , что у - функция аргументов x1, x2, …,xN. Важнейшая особенность булевых функций состоит в том, что они, как и их аргументы, принимают свои значения из двухэлементного множества {0,1}, или (И, Л}, т. е. характеризуются одним из двух возможных состояний.
Функции небольшого числа переменных можно задавать с помощью таблиц, подобных таблицам сложения и умножения одноразрядных чисел. Для этого нужно только указать значения функции для каждой комбинации значений ее аргументов. Основными в двузначной логике являются следующие три функции.
Отрицание - функция у = f(х), принимающая значения 1, когда х = 0, и значение 0, когда х = 1; она обозначается у = 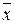 (читается «не х»).
(читается «не х»).
Дизъюнкция — функция у = f(x1, x2), принимающая значение 0 тогда и только тогда, когда оба аргумента имеют значение 0; она обозначается у = x1 \/ x2 (читается «у = x1 или x2»).
Конъюнкция—функция у = f(x1, x2), принимающая значение 1 тогда и только тогда, когда оба аргумента имеют значение 1; она обозначается у = x1 /\ x2 («у = x1 и x2»).
Таблицы для этих функций имеют вид:
| x1 \/ x2 | x1 /\ x2 | ||||||
| x1 | x2 | x1 | x2 | ||||
| x | 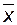
| ||||||
Логические операции и формулы.Булевы функции можно рассматривать как логические операции над величинами, принимающими два значения - 0 и 1. Отрицание - это одноместная операция, а дизъюнкция и конъюнкция — двухместные операции. При этом выражения 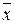 , x1 \/ x2, x1 /\ x2 являются логическими формулами.
, x1 \/ x2, x1 /\ x2 являются логическими формулами.
Более сложные формулы получаются замещением входящих в них переменных другими логическими формулами, которые обычно заключаются в скобки. Например, положив x1 = 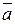 и x2 = b /\ c из x1 V x2,имеем (
и x2 = b /\ c из x1 V x2,имеем ( 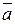 ) \/ (b
) \/ (b 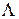 c). Каждая формула определяет некоторую булеву функцию. Ее значение при различных значениях переменных определяется на основании таблиц функций, приведенных в (2). Так, при а = 0, b = 1 и с = 0 имеем:
c). Каждая формула определяет некоторую булеву функцию. Ее значение при различных значениях переменных определяется на основании таблиц функций, приведенных в (2). Так, при а = 0, b = 1 и с = 0 имеем:
x1 = 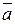 =
= 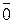 =1, x2 = b /\ с = 1 /\ 0 = 0 и x1 \/ x2 =
=1, x2 = b /\ с = 1 /\ 0 = 0 и x1 \/ x2 = 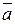 \/ (b \/ c) = 1 \/ 0 = 1. Аналогично получаем значения функции и при других комбинациях значений аргументов.
\/ (b \/ c) = 1 \/ 0 = 1. Аналогично получаем значения функции и при других комбинациях значений аргументов.
Две функции (как и определяющие их формулы) считаются равносильными,если при любых значениях аргументов эти функции (формулы) принимают одинаковые значения. Равносильные функции соединяются знаком равенства, например: (х /\ у) \/ 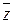 = (
= ( 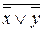 ) /\ z или ((х \/
) /\ z или ((х \/ 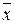 ) /\ у) \/ (у \/ х) == х \/ у. Равносильность функций проверяется по таблицам основных операций, причем необходимо сравнить их значения для всех комбинаций значений переменных.
) /\ у) \/ (у \/ х) == х \/ у. Равносильность функций проверяется по таблицам основных операций, причем необходимо сравнить их значения для всех комбинаций значений переменных.
Множество всех булевых функций вместе с операциями отрицания, конъюнкции и дизъюнкции образует булеву алгебру.
На основе определения основных операций нетрудно убедиться в справедливости следующих тождеств (свойств) булевой алгебры:
коммутативность
х \/ y = y \/ х, х /\ y = y /\ х;
ассоциативность
х \/ ( y \/ z) = (х \/ y) \/ z, х /\ ( y /\ z) = (х /\ y) /\ z;
дистрибутивность
х /\ ( y \/ z) = (х /\ y) /\ (х \/ z), х \/ ( y /\ z) = (х /\ y) /\ (х \/ z);
свойство констант
х \/ 0 = x, х /\ 1 = x;
свойство отрицания
х \/ 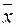 = 1, х /\
= 1, х /\ 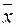 = 0.
= 0.
Приведенные свойства позволяют получить ряд других важных законов и тождеств уже без обращения к таблицам соответствия: 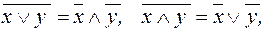 (законы де Моргана), х \/ (х /\ у) = х /\ (х \/ у) = х (законы поглощения) х \/ х = х /\ х = х (законы идемпотентности), а также тождества
(законы де Моргана), х \/ (х /\ у) = х /\ (х \/ у) = х (законы поглощения) х \/ х = х /\ х = х (законы идемпотентности), а также тождества 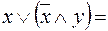 x \/ y; (x /\ y) \/ (x /\ z) \/ (x /\
x \/ y; (x /\ y) \/ (x /\ z) \/ (x /\ 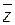 ); = (x /\ z) \/ (y /\
); = (x /\ z) \/ (y /\ 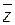 );
); 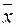 = x;
= x; 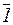 = 0;
= 0;
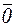 = 1; x \/ 1 =1; x /\ 0 = 0 и т. д.
= 1; x \/ 1 =1; x /\ 0 = 0 и т. д.
Так, законы идемпотентности доказываются следующими преобразованиями:
х \/ х = (х \/ х) /\ 1 = (х \/ х) /\ (х \/ 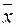 ) = х \/ (х /\ (х \/ х)) = х \/ 0 = х;
) = х \/ (х /\ (х \/ х)) = х \/ 0 = х;
х /\ х = (х /\ х) \/ 0 = (х /\ х) \/ (х /\ 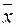 ) = х /\ (х \/
) = х /\ (х \/ 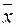 ) = х /\ 1 = х.
) = х /\ 1 = х.
Используя полученные соотношения, имеем:
х \/ 1 = x \/ ( x \/ 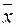 ) = (х \/ х) \/
) = (х \/ х) \/ 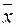 = х \/
= х \/ 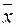 = 1; x /\ 0 = x /\ ( x /\
= 1; x /\ 0 = x /\ ( x /\ 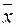 ) = x /\
) = x /\ 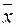 = 0.
= 0.
Доказательство законов поглощения имеет вид:
x \/ (x /\ y) = (x /\ 1) \/ (x /\ y) = x /\ (1 /\ y) = x /\ 1 = x;
x /\ (x \/ y) = (x \/ 0) /\ (x \/ y) = x \/ (y /\ 0) = x \/ 0 = x.
Соотношение 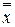 = х доказывается следующим образом:
= х доказывается следующим образом:
из х \/ 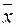 = 1 по закону коммутативности следует
= 1 по закону коммутативности следует 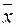 \/ x = 1, откуда сравнением с
\/ x = 1, откуда сравнением с 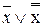 = 1 имеем х =
= 1 имеем х = 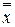 .
.
Интересно доказательство закона де Моргана. На основании свойств отрицания равенство функций 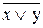 и
и 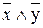 должно означать, что
должно означать, что
(х \/ у) \/ ( 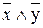 ) = 1 и (х \/ у) \/ (
) = 1 и (х \/ у) \/ ( 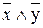 ) = 0.
) = 0.
Действительно,
(х \/ у) \/ ( 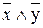 ) = ((х \/ у) \/
) = ((х \/ у) \/ 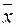 ) /\ ((х \/ у) \/
) /\ ((х \/ у) \/ 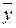 ) = (( x /\
) = (( x /\ 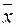 ) \/ y ) /\ (x \/ (y \/
) \/ y ) /\ (x \/ (y \/ 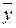 )) =
)) =
= (1 \/ y) /\ (x \/ 1) = 1 /\ 1 = 1, а также
(х \/ у) /\ ( 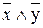 ) = (х /\ \/ (
) = (х /\ \/ ( 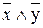 ) = (у /\ (
) = (у /\ ( 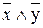 ) = ((x /\
) = ((x /\ 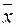 ) /\
) /\ 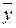 ) \/ ((y /\
) \/ ((y /\ 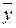 ) /\
) /\ 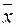 ) =
) =
= (0 /\ 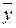 ) \/ (
) \/ ( 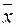 /\ 0) = 0 \/ 0 = 0.
/\ 0) = 0 \/ 0 = 0.
Следовательно, соотношение 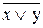 =
= 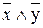 доказано. Аналогично доказывается и второй закон.
доказано. Аналогично доказывается и второй закон.
Упрощение записи формул.Операции дизъюнкции и конъюнкции удовлетворяют законам коммутативности и ассоциативности. Поэтому если переменные или формулы связаны только посредством одной из этих операций, то их можно выполнять в лгсбом порядке, а формулы записывать без скобок. Например:
((х1 \/ x2) \/ (х3 \/ x4) \/ х5 = х1 \/ x2 \/ х3 \/ x4 \/ х5,
а также (х1 /\ x2) /\ (x3 /\ (х4 /\ x5) = х1 /\ x2 /\ x3 /\ х4 /\ x5.
Если считать, что операция конъюнкции должна предшествовать операции дизъюнкции (конъюнкция связывает сильнее дизъюнкции), то можно опустить скобки, в которые заключены формулы со знаком конъюнкции. При наличии скобок в первую очередь должны выполняться операции внутри скобок, независимо от их старшинства. Обычно опускают также скобки, в которые заключены формулы со знаком отрицания.
Еще одно упрощение связано с символикой. Знак конъюнкции в формулах можно опустить и вместо х /\ у писать ху. Операцию конъюнкции часто называют логическим умножением, а операцию дизъюнкции - логическим сложением.
С учетом приведенных условий запись существенно упрощается. Например, формуле (x /\ (y /\ 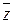 )) \/ ((
)) \/ (( 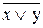 ) /\ z) соответствует запись
) /\ z) соответствует запись 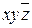 \/
\/ 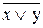 z.
z.
Переключательные схемы. В качестве одной из интерпретаций булевых функций рассмотрим электрическую схему, состоящую из источника напряжения (батареи), лампочки и одного или двух ключей (х1 и x2). Ключи управляются кнопками с двумя состояниями: кнопка нажата (1) и кнопка отпущена (0). Если в исходном состоянии ключ разомкнут, то при нажатии кнопки он замыкается.
Ключ может быть сконструирован и так, что в исходном состоянии он замкнут, тогда нажатие кнопки означает его размыкание, т. е. приводит к противоположному результату. Поэтому нормально замкнутые ключи обозначим через 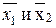 .
.
При соответствующих состояниях кнопок лампочка принимает одно из двух состояний: горит (1) и не горит (0). Состояния кнопок отождествляются со значениями булевых переменных х1 и x2, а состояние лампочки — со значением функций этих переменных.
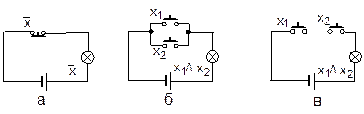
| Рис. 17. Переключательные схемы, соответствующие операциям отрицания (а), дизъюнкции (б) и конъюнкции (в) |
Операции отрицания соответствует схема с одним нормально замкнутым ключом (рис. 17, а). Если кнопка нажата (х = 1), ключ разомкнут и лампочка не горит, т. е. f(х) = 0; при отпущенной кнопке (х = 0) ключ замкнут и лампочка горит, т. е. f(x) = 1. Операциям дизъюнкции и конъюнкции соответствуют схемы с двумя нормально разомкнутыми ключами (рис. 17, б, в). Легко убедиться, что в схеме рис. 17, б лампочка горит при нажатии хотя бы одной из кнопок, а в схеме рис. 17, в - только при нажатии обеих кнопок одновременно.
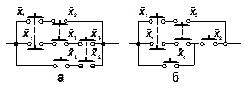
| Рис. 18. Переключательная схема, реализующая логическую функцию (а), и упрощенная схема(б). |
Любую сложную булеву функцию можно представить некоторой переключательной схемой. На рис. 18,а показана схема, реализующая функцию у = х1 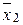 \/
\/ 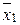 x2x3 \/ x3x4. Та же функция представляется равносильной формулой у = х1
x2x3 \/ x3x4. Та же функция представляется равносильной формулой у = х1 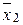 \/ (
\/ ( 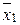 x2 \/ x4)x3, которой соответствует другая более простая схема (рис. 18, б). Следует иметь в виду, что ключи, обозначенные одинаковыми буквами (х или
x2 \/ x4)x3, которой соответствует другая более простая схема (рис. 18, б). Следует иметь в виду, что ключи, обозначенные одинаковыми буквами (х или 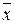 ), связаны между собой и управляются общей кнопкой.
), связаны между собой и управляются общей кнопкой.
В реальных устройствах используются ключи различной конструкции и физической природы (механические, электромагнитные, электронные, гидравлические, пневматические и т. д.) Однако при реализации логических функций многие технические особенности не имеют значения. Существенными свойствами контактных схем являются исходные положения ключей (нормально разомкнуты или нормально замкнуты) и способ их соединения между собой и внешними устройствами. Эта информация полностью отображается графом, ребра которого соответствуют ключам, а вершины - точкам их соединения. Ребра нормально разомкнутых ключей обозначаются соответствующей переменной (х), а нормально замкнутых - отрицанием переменной (х). Например, контактная схема (рис. 23, б) изображается графом, как показано на рис. 19, а.
При изображении контактных схем графами принимаются некоторые специфические условия и упрощения. Обычно переменные обозначаются в разрывах линий, изображающих ребра.
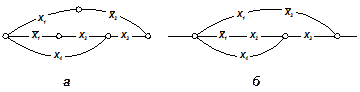
| Рис. 19. Граф переключательной схемы (а) и его упрощенное изображение (б). |
При этом ребрами считаются только такие линии, которые обозначены какой-либо переменной или ее отрицанием. Другие линии, не являющиеся ребрами графа, могут изображать входы и выходы схемы, связи с другими схемами и т. п. Кроме того, вершины второй степени могут не изображаться, так как им инцидентны пары последовательно соединенных ребер, из которых каждое обозначено соответствующей переменной.
На рис. 19,б показана контактная схема в обычно принятом виде.
Высказывания.Пусть х1 и x2 - некоторые высказывания, которые могут быть истинными (1) или ложными (0), например: «Я пойду в театр» (х1) и «Я встречу друга» (x2). Дизъюнкцией х1 \/ x2 является сложное высказывание «Я пойду в театр или встречу друга», а конъюнкцией х1 /\ x2 - высказывание «Я пойду в театр и встречу друга».
Ясно, что если высказывание истинно, то его отрицание ложно. Сложное высказывание, образованное дизъюнкцией двух высказываний, истинно при условии, что истинно хотя бы одно из них. Сложное высказывание, образованное конъюнкцией двух истинных высказываний истинно, если истинны оба эти высказывания одновременно.
Итак, высказывания можно рассматривать как двоичные переменные, а связки «не», «или», «и», с помощью которых образуются сложные высказывания, - как операции над этими переменными. В алгебре высказываний используются еще две операции: импликация х1 → x2, соответствующая связке «если, то» и эквиваленция х1 ~ x2, соответствующая связке «если и только если». Они задаются следующими таблицами:
| x1 ® x2 | x1 ~ x2 | ||||
| x1 | x2 | x1 | x2 | ||
В нашем примере импликацией будет высказывание: «Если пойду в театр, то встречу друга», а эквиваленцией – пойду в театр, если и только если встречу друга». Как видно из таблиц, импликация высказываний ложна только в случае, когда первое из простых высказываний истинно, а второе ложно. Эквиваленция является истинным высказыванием, если оба простые высказывания истинны или ложны одновременно.
Обозначив буквами простые высказывания, можно представить сложное высказывание формулой с помощью соответствующих связок. Например, высказыванию «Если давление масла на шарик клапана больше усилия его пружины (х1), то масло открывает клапан (х2) и частично перетекает из нагнетательной полости во впускную (х3)» соответствует формула х1 → х2 х3.
Предикаты. Обычно высказывания выражают свойства одного или нескольких объектов. Содержательная часть высказывания играет роль определяющего свойства совокупности объектов, для которых это высказывание истинно, и называется предикатом. Например, высказывание «Иванов - отличник» истинно или ложно в зависимости от оценок, которые имеет данный студент. В то же время предикат «х - отличник» определяет подмножество отличников на некотором множестве студентов (группа, курс, факультет). Подставив вместо х фамилии студентов, получим множество высказываний. Совокупность истинных высказываний и будет соответствовать подмножеству отличников.
Предикат представляет собой логическую функцию Р(х), принимающую, как и булевы функции, значение 0 или 1, но в отличие от них, значения аргумента х выбираются из некоторого множества М объектов (х 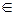 М). В общем случае такая функция может зависеть от многих аргументов х1, х2, . . .,хn, принимающих значения из одного и того же или различных множеств. Ее записывают Р(х1, х2, . . .,хn) и называют n-местным предикатом. Например: «х - четное число», «х - компонент цепи» - одноместные предикаты Р(х);
М). В общем случае такая функция может зависеть от многих аргументов х1, х2, . . .,хn, принимающих значения из одного и того же или различных множеств. Ее записывают Р(х1, х2, . . .,хn) и называют n-местным предикатом. Например: «х - четное число», «х - компонент цепи» - одноместные предикаты Р(х);
«х брат у», «х меньше у» — двуместные предикаты Р(х, у); «х и у - родители z»,
«х - сумма y и z» - трехместные предикаты Р(х, y, z) и т. д. Если аргументы х1, х2, ... ,хn замещены конкретными значениями (объектами), то предикат переходит в высказывание, которое рассматривают как 0 - местный предикат.
Так как предикаты способны принимать только значения 0 и 1, то их, как и булевы переменные, можно связывать логическими операциями. В результате получаем формулы, определяющие более сложные предикаты. Так, если Р(х) означает «х - инженер», а Q(х) - «x - сотрудник нашего отдела», то Р(х) /\ Q(х) = R(х) есть одноместный предикат «х - инженер и сотрудник нашего отдела» или проще «х - инженер нашего отдела». Очевидно, если Р - множество инженеров, а 0 - множество сотрудников данного отдела, то этот предикат соответствует пересечению Р 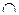 Q. Таким образом, имеет место тесная связь между логикой предикатов и операциями над множествами.
Q. Таким образом, имеет место тесная связь между логикой предикатов и операциями над множествами.
Однородные функции. Если аргументы принимают значения из того же множества, что и сама функция, то ее называют однородной функцией. В этом случае X1 = Х2 = ... = Хn = N и однородная функция, рассматриваемая как закон композиции 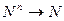 определяет некоторую п-местную операцию на конечном множестве N.
определяет некоторую п-местную операцию на конечном множестве N.
Областью определения однородной функции у = f(х1, х2, ..., xn) служит множество наборов (х1, х2, ..., xn), называемых словами, где каждый из аргументов х1, х2, ..., xn замещается буквами k-ичного алфавита {0, 1, ..., k -1}. Количество п букв в данном слове определяет его длину.
Очевидно, число всевозможных слов длины n в k-ичном алфавите равно kn. Так как каждому такому слову имеется возможность предписать одно из k значений множества N, то общее количество однородных функций от п переменных выражается числом k(kn).
Если буквами алфавита служат числа от 0 до k - 1, то каждое слово (х1, х2, ..., xn) символически представляется упорядоченной последовательностью п таких чисел и рассматривается как запись n-разрядного числа в позиционной системе счисления с основанием k, т. е. x1kn -1 + x2kn –2 + … + xn -1k1 + xnk0. Числа q = = 0, 1, ..., kn - 1 служат номерами слов и тем самым на множестве всех слов вводится естественная упорядоченность (отношение строгого порядка). Аналогично номерами функций можно считать kn -разрядные числа в той же системе счисления.
Различные слова длины п в данном алфавите образуются как n-перестановки с повторениями (2. 10. 1). Так, в трехзначном алфавите {0, 1, 2} словами длины 4 будут все четырехразрядные числа с основанием k = 3, т. е. 0000, 0001, 0002, 0010, 0011, ..., 2221, 2222, которые соответствуют десятичным числам от 0 до 80 = 2 • З3+ 2 • З2+ 2 • З1 + 2 • 30. Поставив каждому такому четырехразрядному числу в соответствие одну из букв алфавита {0, 1, 2}, получим некоторую функцию четырех переменных fi(х1, х2, x3, x4), причем количество таких функций выражается огромным числом 381.
Пусть алфавит состоит из трех букв русского алфавита {о, п, т}. Множество пятибуквенных слов в этом алфавите состоит из 35 = 243 элементов. Наряду с такими имеющими прямой смысл словами, как «топот» и «потоп», оно также включает все другие 5-перестановки, например: «ооппт», «поппп», «тттоп» и др.
Примерами однородных логических функций двух переменных могут служить операции сложения и умножения одноразрядных m-значных чисел по модулю т (2. 8. 7), внутренние операции поля Галуа (2. 8. 9) с четырехзначным алфавитом {0, 1, А, В} и т. п.
Табличное задание функций. Как и бинарный закон композиции (2. 7. 2), однородная функция двух переменных может быть задана таблицей соответствия (матрицей), строки и столбцы которой соответствуют буквам алфавита. Таким способом представлялись функции одной и двух переменных в (1. 5. 2),(1. 5. 8) и (1. 5. 10). Для представления функций трех и большего числа переменных потребовались бы трехмерные и, вообще, n-мерные таблицы. Этого можно избежать, если столбцы матрицы поставить в соответствие не буквам алфавита, а словам, т. е. образовать kn столбцов. Для каждой функции отводится строка, клетки которой заполняются буквами из данного алфавита. Матрица всех функций п переменных в k-значном алфавите содержит 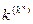 строк и называется общей таблицей соответствия. Например, для k = 3 и п = 2 такая матрица имеет вид:
строк и называется общей таблицей соответствия. Например, для k = 3 и п = 2 такая матрица имеет вид:
| x1 x2 | |||||||||
| y0 y1 y2 … y2361 … y19682 | . . | . . | . . | . . | . . | . . | . . | . . | . . |
Номера столбцов определяются расположенными над ними n-разрядными числами с основанием k, каждое из которых читается сверху вниз. Номера функций отождествляются с kn-разрядными числами, которые соответствуют строкам матрицы в той же системе счисления.
Двузначные однородные функции. Наиболее простым и в то же время важнейшим классом однородных функций являются двузначные (булевы) функции, частично рассмотренные в (1.5. 2) и последующих пунктах.
Областью определения булевых функций от п переменных служит множество слов длины п. Они представляют собой всевозможные наборы из п двоичных цифр и их общее количество равно 2n.
Число всевозможных булевых функций п переменных v = 2n быстро возрастает с увеличением п (при п = 3 оно равно 256, а при п = 5 превышает 4 миллиарда). Но функции одной и двух переменных еще можно перечислить и подробно исследовать, так как их количество сравнительно невелико (v = 4 при п = 1 и v = 16 при п = 2).
Булевы функции одной переменной. Общая таблица соответствия для булевых функций одной переменной имеет вид (справа указаны обозначения функций):
| x | y | ||
| y0 | |||
| y1 | x | ||
| y2 | 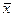
| ||
| y3 |
Две функции у0 = 0 и у3 = 1 представляют собой функции-константы (тождественный нуль и тождественная единица), таккакони не изменяют своих значений при изменении аргумента. Функция y1 = х повторяет значения переменной х и потому просто совпадает с ней.
Единственной нетривиальной функцией является у2 = 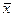 , называемая отрицанием или инверсией (
, называемая отрицанием или инверсией ( 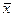 читается «не х»). Она равна 1, когда аргумент принимает значение 0, и равна 0 при аргументе 1.
читается «не х»). Она равна 1, когда аргумент принимает значение 0, и равна 0 при аргументе 1.
Булева алгебра
Булевы функции двух переменных. Все 16 функций двух переменных приведены в табл. 6, где указаны условные обозначения, названия и чтения функций (в скобках даны встречающиеся в литературе варианты).
Шесть из приведенных функций не зависят от x1 или x2 (или от обоих вместе). Это две константы (у0 = 0 и у15 = 1), повторения (у3 = х1 и у5 = х2) и отрицания (у10 = 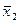 и у12 =
и у12 = 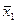 ), являющиеся функциями одной переменной (х1 или x2). Из остальных десяти функций две (y4 и y11) отличаются от соответствующих им (y2 и y13) лишь порядком расположения аргументов и поэтому не являются самостоятельными. Поэтому из 16 булевых функций двух переменных только восемь являются оригинальными (у1, у2, у6, у7, у8, у9, у13, у14).
), являющиеся функциями одной переменной (х1 или x2). Из остальных десяти функций две (y4 и y11) отличаются от соответствующих им (y2 и y13) лишь порядком расположения аргументов и поэтому не являются самостоятельными. Поэтому из 16 булевых функций двух переменных только восемь являются оригинальными (у1, у2, у6, у7, у8, у9, у13, у14).
Рассмотрение булевых функций одной, двух и большего числа переменных показывает, что всякая функция от меньшего числа переменных содержится среди функций большего числа переменных. Функции, которые сводятся к зависимости от меньшего числа переменных, называют вырожденными, а функции, существенно
Таблица 6
Булевые функции двух переменных
| x1 x2 | 0 0 1 1 0 1 0 1 | Обозначения | Названия | Чтение |
| y0 | 0 0 0 0 | Константа 0 (тождественный нуль, всегда ложно) | Любое 0 | |
| y1 | 0 0 0 1 | x1x2; 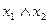 (
( 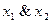 ; ; 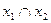 ) )
| Конъюнкция (совпадение, произведение, пересечение, логическое «и») | x1 и x2 (и x1 и x2) |
| y2 | 0 0 1 0 | 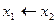 (
( 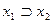 ; ; 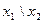 ) )
| Отрицание импликации (совпадение с запретом, антисовпадение, запрет) | x1, но не x2 |
| y3 | 0 0 1 1 | X1 | Повторение (утверждение, доминация) первого аргумента | Как x1 |
| y4 | 0 1 0 0 | 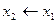 (
( 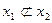 ; ; 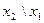 ) )
| Отрицание обратной импликации (обратное антисовпадение) | Не x1, но x2 |
| y5 | 0 1 0 1 | x2 | Повторение (утверждение, доминация) второго аргумента | Как x2 |
| y6 | 0 1 1 0 | x1 + x2
( 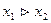 ; ; 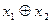 ) )
| Сумма по модулю 2 (неравнозначность, антиэквивалентность) | x1 не как x2 (или x2 или x1) |
| y7 | 0 1 1 1 | 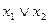 (x1 + x2;
(x1 + x2; 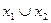 ) )
| Дизъюнкция (разделение, логическая сумма, сборка, логическое «или») | x1 или x2 (x1 или хотя бы x2) |
| y8 | 1 0 0 0 | 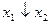 (
( 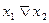 ; ; 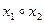 ) )
| Стрелка Пирса (функция Вебба, отрицание дизъюнкции, логическое «не – или») | Ни x1,ни x2 |
| y9 | 1 0 0 1 | x1 ~ x2
( 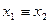 ; ; 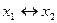 ) )
| Эквиваленция (равнозначность, эквивалентность, взаимозависимость) | x1 как x2 (x1, если и только если x2) |
| y10 | 1 0 1 0 | 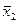 (x2; ~x2;
(x2; ~x2; 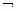 x2) x2)
| Отрицание (инверсия) второго аргумента (дополнение к первой переменной) | Не x2 |
| y11 | 1 0 1 1 | 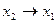 (
( 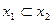 ; ; 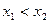 ) )
| Обратная импликация (обратное разделение с запретом, обратная селекция) | Если x2, то x1 (x1 или не x2) |
| y12 | 1 1 0 0 | 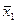 (x1; ~x1;
(x1; ~x1; 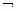 x1) x1)
| Отрицание (инверсия) первого аргумента (дополнение к первой переменной) | Не x1 |
| y13 | 1 1 0 1 | 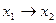 (
( 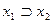 ; ; 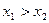 ) )
| Импликация (разделение с запретом, следование, селекция) | Если x1, то x1 (не x1 или x2) |
| y14 | 1 1 1 0 | x1 / x2
( 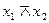 ; ; 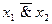 ) )
| Штрих Шеффера (отрицание конъюнкции, несовместность, логическое «не – и») | Не x1 или не x2 |
| y15 | 1 1 1 1 | Константа 1 (тождественная единица, всегда истино) | Любое 1 |
зависящиеот всех переменных, являются невырожденными. Так, среди функций одной переменной имеются две вырожденные (константы 0 и 1, которые можно рассматривать как функции от нуля переменных), функции двух переменных содержат те же константы и четыре функции одной переменной и т. д.
Зависимость между булевыми функциями.Из табл. 6 видно, что между функциями имеются зависимости 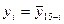 (i = 0, 1, ... ..., 15), на основании которых можно записать соотношения для констант
(i = 0, 1, ... ..., 15), на основании которых можно записать соотношения для констант 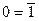 и
и 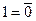 , для функции одной переменной х =
, для функции одной переменной х = 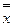 и для функций двух переменных:
и для функций двух переменных:
x1x2 = 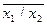 ;
; 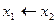 =
= 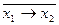 ; x1 + x2 =
; x1 + x2 = 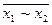 ;
; 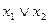 =
= 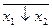 ,
,
или
x1/x2 = 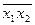 ;
; 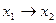 =
= 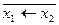 ; x1 ~ x2 =
; x1 ~ x2 = 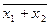 ;
; 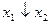 =
= 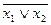 .
.
Из этих зависимостей следует, что любая функция двух переменных (включая константы) выражается в аналитической форме через совокупность шести функций, содержащей отрицание 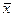 и любую из каждой пары функций {y0, y15},{y1, y14},{y2, y13}, {y6, y9}, {y7, y8}. Например, такой совокупностью могут служить функции: константа 0, отрицание`х, конъюнкция х1x2, дизъюнкция
и любую из каждой пары функций {y0, y15},{y1, y14},{y2, y13}, {y6, y9}, {y7, y8}. Например, такой совокупностью могут служить функции: константа 0, отрицание`х, конъюнкция х1x2, дизъюнкция 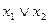 ,эквиваленция х1 ~ x2 и импликация
,эквиваленция х1 ~ x2 и импликация 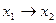 . Как уже упоминалось в (1. 5. 8), они используются в исчислении высказываний.
. Как уже упоминалось в (1. 5. 8), они используются в исчислении высказываний.
Выбранная таким способом совокупность шести функций является избыточной. Можно показать, что импликация и эквиваленция выражаются через остальные функции этой совокупности:
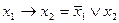 ;
;
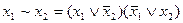 .
.
Для этого достаточно построить таблицу соответствия и сравнить ее с табл. 6:
| x1 x2 | |||||
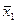
| |||||
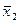
| |||||
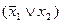
| 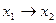
| ||||
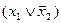
| |||||
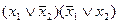
| 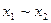
|
Таким образом, комплект элементарных функций сокращается до четырех: константа 0, отрицание 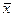 , конъюнкция x1x2 и дизъюнкция
, конъюнкция x1x2 и дизъюнкция 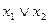 . Этот комплект обладает существенными удобствами и часто применяется на практике, но и он может быть сокращен. Так, из законов де Моргана и свойства двойного отрицания вытекают тождества:
. Этот комплект обладает существенными удобствами и часто применяется на практике, но и он может быть сокращен. Так, из законов де Моргана и свойства двойного отрицания вытекают тождества:
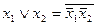 ; x1x2 =
; x1x2 = 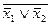 .
.
Отсюда следует, что булевы функции выражаются через отрицание и конъюнкцию или через отрицание и дизъюнкцию.
Более того, для записи любой булевой функции достаточно только одной из двух элементарных функций — стрелки Пирса или штриха Шеффера. Это вытекает из соотношений (их доказательство приводится аналогично с помощью таблиц соответствия):
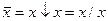 ;
;
x1x2 = (x1/x2)/(x1/x2); 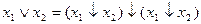 .
.
Булевы функции многих переменных. С помощью суперпозиции функций, т. е. подстановки в логические формулы вместо переменных некоторых булевых функций, можно получить более сложные функции от любого числа переменных. Например, подставляя в выражение аb формулы 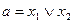 и
и 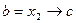 , а также
, а также 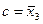 , получаем
, получаем 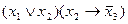 . Таблица соответствия для сложных формул записывается на основании общей таблицы для элементарных функций. Для данного примера она имеет вид:
. Таблица соответствия для сложных формул записывается на основании общей таблицы для элементарных функций. Для данного примера она имеет вид:
| x1 x2 x3 | ||||||||
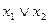
| ||||||||
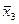
| ||||||||
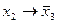
| ||||||||
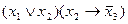
|
Если на всех наборах значений переменных функция принимает значение 0 или 1, то она вырождается в соответствующую константу и называется тождественным нулем или тождественной единицей.
Например, 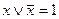 ;
; 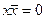 ;
; 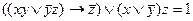 ;
; 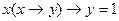 и т. п.
и т. п.
Дата добавления: 2016-02-02; просмотров: 1836;
