Позиционные системы счисления.
В настоящее время в цифровых системах управления для кодирования переменных, адресов и команд находят применение следующие системы счисления: шестнадцатеричная, двоичная, восьмеричная и, естественно, десятичная системах счисления.
Изучение систем счисления относится к сфере дискретной математики, так как в основе каждой системы счисления лежит некоторое конечное дискретное множество цифр.
Все перечисленные выше системы счисления относятся к позиционным системам счисления, в которых доля, вносимая цифрой в число, зависит от ее позиции в числе. В любой позиционной системе счисления некоторое число, содержащее n цифр, может быть представлено как
xn xn-1 ...x2 x1 x0 = xn× an+xn-1× an +...+x2× a2 +x1× a1 +x0× a0
Здесь число а называют основанием системы счисления.
Например, в двоичной системе счисления:
10a= 1× a1 +0× a0 = a
Легко показать, что в любой системе счисления число 10 равно основанию системы счисления а.
Двоичная система счисления не всегда хорошо читается человеком, поэтому при кодировании двоичные числа часто представляют шестнадцатеричными или восьмеричными числами, для которых возможен прямой перевод в двоичную систему счисления по тетрадам (четверкам) для шестнадцатеричной или триадам (тройкам) для восьмеричной системы счисления. Перевод шестнадцатеричных цифр в двоичные приведен в таблице.
| Десятичные числа | Шестнадцатеричные цифры | Двоичные числа | Восьмеричные числа | Двоично-десятичные числа |
| 0 | 0 | 0000 | 0 | 0000 |
| 1 | 1 | 0001 | 1 | 0001 |
| 2 | 2 | 0010 | 2 | 0010 |
| 3 | 3 | 0011 | 3 | 0011 |
| 4 | 4 | 0100 | 4 | 0100 |
| 5 | 5 | 0101 | 5 | 0101 |
| 6 | 6 | 0110 | 6 | 0110 |
| 7 | 7 | 0111 | 7 | 0111 |
| 8 | 8 | 1000 | 10 | 1000 |
| 9 | 9 | 1001 | 11 | 1001 |
| 10 | A | 1010 | 12 | 0001 0000 |
| 11 | B | 1011 | 13 | 0001 0001 |
| 12 | C | 1100 | 14 | 0001 0010 |
| 13 | D | 1101 | 15 | 0001 0011 |
| 14 | E | 1110 | 16 | 0001 0100 |
| 15 | F | 1111 | 17 | 0001 0101 |
Рассмотрим простейшие арифметические действия в различных системах счисления.
Даны два шестнадцатеричных числа: ВD+19
ВD= В× 161+D× 160=1110×16+1310=18910
1916= 1× 161+9× 160=2510
18910+2510=21410
21410=1310×16+6 =D6
D + 9 = 1310 + 9 = 22, поскольку 22>15, требуется перенос в старший разряд
22 = 1610 + 6 =1616
B + 1 + 1 = D
в результате получаем
| 1 | ||
| B | D | |
| + | 1 | 9 |
| D | 6 |
В двоичной системе счисления:
В= 10112
D= 11012
1 = 00012
9 = 10012
ВD= 1011 11012
1916=0001 10012
| 1 | 1 | 1 | 1 | |||||
| 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | |
| + | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 |
11012 = D
01102 = 6
1101 01102 = D6
В восьмеричной системе счисления
ВD= 1011 11012 = 010 _ 111 _ 1012
0102 = 2
1112 = 7
1012 = 5
ВD = 2758
1916=0001 10012 = 000 _ 011 _ 0012
0002 = 0
0112 = 3
0012 = 1
1916 = 318
2758 + 318
Осуществим поразрядное сложение
5 + 1 = 68
7 + 3 = 1010 , поскольку 10>7 требуется перенос в старший разряд
1010 = 810 + 2 = 128
2 + 1 = 38
В результате получим
| 1 | |||
| 2 | 7 | 5 | |
| + | 3 | 1 | |
| 3 | 2 | 6 |
2758 + 318 = 3268
Выполним проверку путем перевода в двоичную и шестнадцатеричную системы
счисления
38 = 0112
28 = 0102
68 = 1102
Отсюда получим
3268 = 011 _ 010 _ 1102 = 1101 _01102 = D616
Достаточно широко используется также двоично-десятичная система счисления, в которой каждая десятичная цифра представляется двоичной тетерадой.
ОСНОВЫ ТЕОРИИ МНОЖЕСТВ
Понятие множества
Что такое множество? Ответить на этот вопрос не так просто, как это кажется на первый взгляд. В повседневной жизни и практической деятельности часто приходится говорить о некоторых совокупностях различных объектов: предметов, понятий, чисел, символов и т. п. Например, совокупность деталей механизма, аксиом геометрии, чисел натурального ряда, букв русского алфавита. На основе интуитивных представлений о подобных совокупностях сформировалось математическое понятие множества как объединения отдельных объектов в единое целое. Именно такой точки зрения придерживался основатель теории множеств немецкий математик Георг Кантор.
Множество относится к категории наиболее общих, основополагающих понятий математики. Поэтому вместо строгого определения обычно принимается некоторое основное положение о множестве и его элементах. Так, группа выдающихся математиков, выступающая под псевдонимом Н. Бурбаки, исходит из следующего положения: «Множество образуется из элементов, обладающих некоторыми свойствами и находящихся в некоторых отношениях между собой или с элементами других множеств».
2. Множество и его элементы. Утверждение, что множество А состоит из различимых элементов 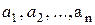 (и только из этих элементов), условно записывается
(и только из этих элементов), условно записывается 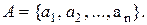 Принадлежность элемента множеству (отношение принадлежности) обозначается символом
Принадлежность элемента множеству (отношение принадлежности) обозначается символом 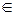 , т. е. a1
, т. е. a1 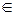 А, a2
А, a2 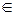 А, … , an
А, … , an 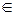 А, или короче
А, или короче 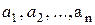
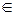 A. Если b не является элементом A, то пишут b
A. Если b не является элементом A, то пишут b 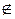 A или b
A или b 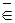 A.
A.
Два множества А и В равны (тождественны), А = В, тогда и только тогда, когда каждый элемент А является элементом В и обратно. Это значит, что множество однозначно определяется своими элементами.
Множество может содержать любое число элементов — конечное или бесконечное. Соответственно имеем конечные (множество цифр О, 1, ..., 9 или страниц в книге) или бесконечные (множество натуральных чисел или окружностей на плоскости) множества. Не следует, однако, связывать математическое понятие «множество» с обыденным представлением о множестве как о большом количестве. Так, единичное (одноэлементное) множество содержит только один элемент. Более того, вводится также понятие пустого множества, которое не содержит никаких элементов. Пустое множество обозначается специальным символом Ø.
Роль пустого множества Ø аналогична роли числа нуль. Это понятие можно использовать для определения заведомо несуществующей совокупности элементов (например, множество зеленых слонов, действительных корней уравнения х2+1=0). Более существенным мотивом введения пустого множества является то, что заранее не всегда известно (или неизвестно вовсе), существуют ли элементы, определяющие какое-то множество. Например, множество выигрышей в следующем тираже спортлото на купленные билеты может оказаться пустым. Никто еще не знает, является ли пустым или нет множество всех решений в целых числах уравнения х3 + у3 + z3 == 30. Без понятия пустого множества во всех подобных случаях, говоря о каком-нибудь множестве, приходилось бы
добавлять оговорку «если оно существует».
Множество и подмножества. Множество A, все элементы которого принадлежат и множеству В, называется подмножеством (частью) множества В. Это отношение между множествами называют включением и обозначают символом 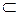 , т. е. А
, т. е. А 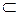 В (А включено в В) или В
В (А включено в В) или В 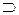 А (В включает А). Например, множество конденсаторов электронной цепи является подмножеством всех ее компонентов, множество положительных чисел — это подмножество множества действительных чисел.
А (В включает А). Например, множество конденсаторов электронной цепи является подмножеством всех ее компонентов, множество положительных чисел — это подмножество множества действительных чисел.
Отношение A 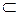 В допускает и тождественность (A=В), т. е. любое множество можно рассматривать как подмножество самого себя (A
В допускает и тождественность (A=В), т. е. любое множество можно рассматривать как подмножество самого себя (A 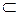 A). Полагают также, что подмножеством любого множества является пустое множество Ø, т. е. Ø
A). Полагают также, что подмножеством любого множества является пустое множество Ø, т. е. Ø 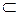 А. Одновременное выполнение соотношения A
А. Одновременное выполнение соотношения A 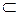 В и B
В и B 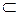 A возможно только при A=В. И обратно A=В, если A
A возможно только при A=В. И обратно A=В, если A 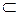 В и B
В и B 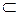 А. Это может служить определением равенства двух множеств через отношение включения.
А. Это может служить определением равенства двух множеств через отношение включения.
Наряду с A 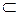 В, в литературе можно встретить и другое обозначение A
В, в литературе можно встретить и другое обозначение A 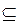 В. При этом под A
В. При этом под A 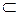 В понимают такое отношение включения, которое не допускает равенства
В понимают такое отношение включения, которое не допускает равенства
A и В (строгое включение). Если допускается А=В, то пишут A 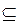 В (нестрогое включение). Мы будем придерживаться принятого ранее обозначения как для строгого, так и для нестрогого включения.
В (нестрогое включение). Мы будем придерживаться принятого ранее обозначения как для строгого, так и для нестрогого включения.
Множество подмножеств.Любое непустое множество А имеет, по крайней мере, два различных подмножества: само А и пустое множество Ø. Эти подмножества называются несобственными, а все другие подмножества А называют собственными (эта терминология связана со словами «собственно подмножества», а не со словом «собственность»). Конечные собственные подмножества образуются всевозможными сочетаниями по одному, два, три и т. д. элементов данного множества.
Элементы множества сами могут являться некоторыми множествами. Например, книга из множества книг в шкафу может рассматриваться как множество страниц. Здесь следует обратить внимание на то, что речь идет об элементах множества, а не о подмножествах (никакая совокупность страниц не может рассматриваться как подмножество множества книг).
Множество, элементами которого являются все подмножества множества А, называют множеством подмножеств (множеством-степенью) А и обозначают через Р(А). Так, для трехэлементного множества А={а, Ь, с} имеем Р(А)={ Ø, {а}, {b}, {c}, {а,b}, {а,c},{c,b},{а,b,c}}.
В случае конечного множества A, состоящего из n элементов, множество подмножеств Р(А) содержит 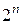 элементов. Доказательство основывается на сумме всех коэффициентов разложения бинома Ньютона или на представлении подмножеств n-раз- рядными двоичными числами, в которых 1 (или 0) соответствует элементам подмножеств.
элементов. Доказательство основывается на сумме всех коэффициентов разложения бинома Ньютона или на представлении подмножеств n-раз- рядными двоичными числами, в которых 1 (или 0) соответствует элементам подмножеств.
Следует подчеркнуть различия между отношением принадлежности и отношением включения. Как уже указывалось, множество A может быть своим подмножеством (A 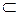 A), но оно не может входить в состав своих элементов (A
A), но оно не может входить в состав своих элементов (A 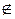 A). Даже в случае одноэлементных подмножеств следует различать множество A={a} и его единственный элемент а. Отношение включения обладает свойством транзитивности: если A
A). Даже в случае одноэлементных подмножеств следует различать множество A={a} и его единственный элемент а. Отношение включения обладает свойством транзитивности: если A 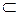 B и B
B и B 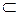 C, то A
C, то A 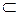 C. Отношение принадлежности этим свойством не обладает. Например, множество A={1, {2,3} ,4} в числе своих элементов содержит множество {2, 3}, поэтому можно записать: 2,3
C. Отношение принадлежности этим свойством не обладает. Например, множество A={1, {2,3} ,4} в числе своих элементов содержит множество {2, 3}, поэтому можно записать: 2,3 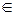 {2, 3} и {2, 3}
{2, 3} и {2, 3} 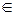 A. Но из этого вовсе не следует, что элементы 2 и 3 содержатся в A (в приведенном примере мы не находим 2 и 3 среди элементов множества A, т. е. 2, 3
A. Но из этого вовсе не следует, что элементы 2 и 3 содержатся в A (в приведенном примере мы не находим 2 и 3 среди элементов множества A, т. е. 2, 3 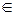 A.
A.
Задание множеств.
Множество 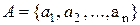 можно задать простым перечислением его элементов. Например, спецификация задает множество деталей изделия, каталог — множество книг в библиотеке. Но этот способ не пригоден для задания бесконечных множеств и даже в случае конечных множеств часто практически нереализуем.
можно задать простым перечислением его элементов. Например, спецификация задает множество деталей изделия, каталог — множество книг в библиотеке. Но этот способ не пригоден для задания бесконечных множеств и даже в случае конечных множеств часто практически нереализуем.
Рассмотрим в качестве примера фасад 16-этажного дома с 38 окнами в каждом этаже. В вечернее время каждое из окон дома может быть освещено или затемнено, т. е. находиться в двух состояниях. Определенные совокупности освещенных окон можно рассматривать как некоторые образы. Считая все окна (их число равно 38*16=608) различными по их расположению на фасаде, каждый такой образ можно связать с соответствующим подмножеством освещенных окон. Тогда количество всех образов равно количеству элементов множества подмножеств всех окон, т. е. 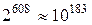 . Полученное число настолько большое, что его трудно даже представить. Оно несравнимо больше числа атомов во всей видимой вселенной, которое равно примерно 1037. Если бы каждый атом превратился во вселенную, то и тогда на один атом приходилось бы 1037 образов 10183 == 1073 *1073 * 1037). Поэтому, хотя множество всех образов конечно и любой из них можно легко определить, о задании подобных множеств перечислением их элементов не может быть и речи.
. Полученное число настолько большое, что его трудно даже представить. Оно несравнимо больше числа атомов во всей видимой вселенной, которое равно примерно 1037. Если бы каждый атом превратился во вселенную, то и тогда на один атом приходилось бы 1037 образов 10183 == 1073 *1073 * 1037). Поэтому, хотя множество всех образов конечно и любой из них можно легко определить, о задании подобных множеств перечислением их элементов не может быть и речи.
Определяющее свойство.Другой способ задания множества состоит в описании элементов определяющим свойством Р(х) (формой от х), общим для всех элементов. Обычно Р(х) — это высказывание, в котором что-то утверждается об х, или некоторая функция переменной х. Если при замене х на а высказывание Р(а) становится истинным или функция в заданной области определения удовлетворяется, то а есть элемент данного множества. Множество, заданное с помощью формы Р(х), обозначается как Х={х | Р(х)}, или Х={х :Р(х)}, причем а 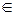 {х | Р(х)}, если Р(а) истинно. Например {х | х2 = 2} - множество чисел, квадрат которых равен двум, {х | х есть животное с хоботом} - множество слонов.
{х | Р(х)}, если Р(а) истинно. Например {х | х2 = 2} - множество чисел, квадрат которых равен двум, {х | х есть животное с хоботом} - множество слонов.
Обычно уже в самом определении конкретного множества явно или неявно ограничивается совокупность допустимых объектов. Так, множество слонов следует искать среди млекопитающих, а не среди рыб и тем более не среди планет. Если речь идет о множестве чисел, делящихся на 3, то ясно, что оно является подмножеством целых чисел. Удобно совокупность допустимых объектов зафиксировать явным образом и считать, что рассматриваемые множества являются подмножествами этой совокупности. Ее называют основным множеством (универсумом) и обычно обозначают через И. Так, универсумом арифметики служат числа, зоологии - мир животных, лингвистики - слова и т.п.
Если множество выделяется из множества A с помощью формы Р(х), то запись
{х | х 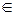 А, Р(х)} часто упрощается: {х
А, Р(х)} часто упрощается: {х 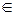 А | Р(х)}. Запись f(х) | Р(х)} означает множество всех таких у=f(х), для которых имеется х, обладающий свойством Р(х). Например, {х2 | х - простое число} означает множество квадратов простых чисел.
А | Р(х)}. Запись f(х) | Р(х)} означает множество всех таких у=f(х), для которых имеется х, обладающий свойством Р(х). Например, {х2 | х - простое число} означает множество квадратов простых чисел.
7. Операции над множествами. Множества можно определять также при помощи операций над некоторыми другими множествами. Пусть имеются два множества A и B.
Объединение (сумма) А 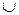 В есть множество всех элементов, принадлежащих A или В. Например, {1, 2, 3}
В есть множество всех элементов, принадлежащих A или В. Например, {1, 2, 3} 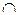 (2, 3, 4} = {1, 2, 3, 4}.
(2, 3, 4} = {1, 2, 3, 4}.
Пересечение (произведение) А 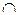 В есть множество всех элементов, принадлежащих одновременно как A, так и В. Например, {1, 2, 3}
В есть множество всех элементов, принадлежащих одновременно как A, так и В. Например, {1, 2, 3} 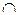 {2, 3, 4} = {2, 3}. Множества, не имеющие общих элементов (A
{2, 3, 4} = {2, 3}. Множества, не имеющие общих элементов (A 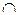 В = Ø), называют непересекающимися (расчлененными).
В = Ø), называют непересекающимися (расчлененными).
Разность А \ В (или A - В) есть множество, состоящее из всех элементов A, не входящих в В, например, {1, 2, 3} \ {2, 3, 4} = {1}. Ее можно рассматривать как относительное дополнение В до A. Если A 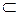 U, то множество U \ A называется абсолютным дополнением (или просто дополнением) множества A и обозначается через A. Оно содержит все элементы универсума U, кроме элементов множества A. Дополнение A определяется отрицанием свойства Р(х), с помощью которого определяется A. Очевидно, А \ В = A
U, то множество U \ A называется абсолютным дополнением (или просто дополнением) множества A и обозначается через A. Оно содержит все элементы универсума U, кроме элементов множества A. Дополнение A определяется отрицанием свойства Р(х), с помощью которого определяется A. Очевидно, А \ В = A 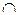 В.
В.
Дизъюнктивная сумма (симметрическая разность) А + В (или A 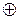 В) есть множество всех элементов, принадлежащих или A, или В (но не обоим вместе). Например, {1, 2, 3} + {2, 3, 4} = {1, 4}. Дизъюнктивная сумма получается объединением элементов множеств за исключением тех, которые встречаются дважды.
В) есть множество всех элементов, принадлежащих или A, или В (но не обоим вместе). Например, {1, 2, 3} + {2, 3, 4} = {1, 4}. Дизъюнктивная сумма получается объединением элементов множеств за исключением тех, которые встречаются дважды.
8. Круги Эйлера. Для наглядного изображения соотношений между подмножествами какого-либо универсума и используют круги Эйлера (рис. 1). Обычно универсум представляется множеством точек прямоугольника, а его подмножества изображаются в виде кругов или других простых областей внутри этого прямоугольника.
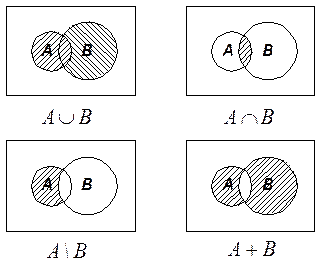
| Рис. 1. Круги Эйлера для основных операций над множествами. |
Множества, получаемые в результате операций над множествами A и В, изображены на рис. 1 заштрихованными областями. Непересекающиеся множества
изображаются неперекрывающимися областями, а включение множества соответствует области, целиком располагающейся внутри другой (рис. 2). Дополнение множества A (до U), т. е. множество 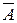 изображается той частью прямоугольника, которая лежит за пределами круга, изображающего A.
изображается той частью прямоугольника, которая лежит за пределами круга, изображающего A.
9. Отношения. В начале этого параграфа речь шла о том, что элементы множества могут находиться в некоторых отношениях между собой или с элементами других множеств.
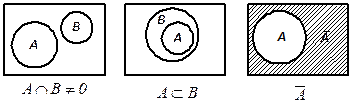
| 2. Круги Эйлера для непересекающихся множеств, отношения включения и дополнения. |
В самом общем смысле отношение означает какую-либо связь между предметами или понятиями. Отношения между парами объектов называют бинарными (двуместными). Выше же были рассмотрены два таких отношения - принадлежность (а 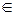 A) и включение A
A) и включение A 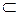 B. Первое из них определяет связь между множеством и его элементами, а второе - между двумя множествами. Примерами бинарных отношений являются равенство (=), неравенства (< или
B. Первое из них определяет связь между множеством и его элементами, а второе - между двумя множествами. Примерами бинарных отношений являются равенство (=), неравенства (< или 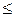 ), а также такие выражения как «быть братом», «делиться (на какое-то число)», «входить в состав (чего-либо)» и т. п.
), а также такие выражения как «быть братом», «делиться (на какое-то число)», «входить в состав (чего-либо)» и т. п.
Для любого бинарного отношения можно записать соответствующее ему соотношение (для отношения неравенства соотношением будет х < у, для отношения «быть братом» соотношение запишется как «х брат у»). В общем виде соотношение можно записать как хАу, где А - отношение, устанавливающее связь между элементом х из множества
Х (х 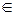 X) и элементом y из множества Y (y
X) и элементом y из множества Y (y 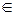 Y). Ясно, что отношение полностью определяется множеством всех пар элементов (х, у), для которых оно имеет место. Поэтому любое бинарное отношение А можно рассматривать как множество упорядоченных пар (х, у).
Y). Ясно, что отношение полностью определяется множеством всех пар элементов (х, у), для которых оно имеет место. Поэтому любое бинарное отношение А можно рассматривать как множество упорядоченных пар (х, у).
Отношения могут обладать некоторыми общими свойствами (например, отношение включения и отношение равенства транзитивны). Определяя эти свойства и комбинируя их, можно выделить важные типы отношений, изучение которых в общем виде заменяет рассмотрение огромного множества частных отношений.
10. Функции как отношения. Функция f, ставящая каждому числу х (аргументу) в соответствие определенное число (значение функции) у=f(х), также является бинарным отношением.
Обобщая это понятие, можно считать функцией такое бинарное отношение f, которое каждому элементу х из множества Х ставит в соответствие один и только один элемент из множества Y, т. е. хfу. При этом считают, что элементами множеств Х и Y могут быть объекты любой природы, а не только числа.
Функцией в таком общем понимании будет, например, соответствие между деталями какого-либо механизма и их массой (каждой детали соответствует ее масса), между человеком и его фамилией и т. п. В то же время такие отношения как неравенство (<) или «быть братом» функциями не являются, так как для каждого числа можно указать бесконечные множества превышающих его чисел, а человек может иметь несколько братьев или совсем их не иметь.
Обобщение понятия функции явилось одним из отправных моментов нового важного раздела современной математики - функционального анализа. Это понятие имеет огромное прикладное значение, так как позволяет рассматривать функциональные отношения между объектами любой природы.
Дата добавления: 2016-02-02; просмотров: 1328;
