НОВЫЙ ЗАКОН ФОРМИРОВАНИЯ ЭЛЕКТРИЧЕСКОЙ МОЩНОСТИ
Все биологические объекты Природы потребляют электрическую энергию, питающую, например, сердце, импульсами. Это самый экономный процесс её потребления. Все источники электрической энергии, изобретённые человеком, производят её непрерывно. Абсолютное большинство этой энергии также потребляется непрерывно и все приборы, учитывающие её расход, настроены на непрерывное напряжение, генерируемое первичными источниками энергии: генераторами электростанций, аккумуляторами и батареями. Так как напряжение и ток являются функциями изменения электрической энергии, то математики первые взялись за решение задачи правильного учёта её расхода. Сейчас мы увидим, как дорого обходится человечеству стремление носителей математических знаний присваивать себе роль судей в достоверности физических знаний. Ниже информация о том, как авторитет математики закрывает возможность выявления физических ошибок с глобальными последствиями.
В системе СИ энергия выражается в Джоулях (Дж). Количество электрической энергии 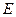 зависит от напряжения
зависит от напряжения 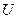 , тока
, тока 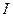 и времени
и времени 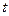 их действия и определяется зависимостью
их действия и определяется зависимостью
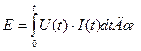 . (23)
. (23)
Чтобы иметь представление о величине энергии, генерируемой в одну секунду, введено понятие мощность. Она определяется по формуле
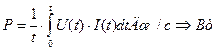 . (24)
. (24)
Когда напряжение и ток непрерывны (рис. 31), то отдельное интегрирование функций напряжения 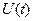 и тока
и тока 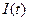 даёт их средние величины:
даёт их средние величины:
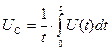 ; (25)
; (25)
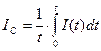 (26)
(26)
и формула для расчёта средней мощности принимает простой вид
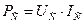 . (27)
. (27)
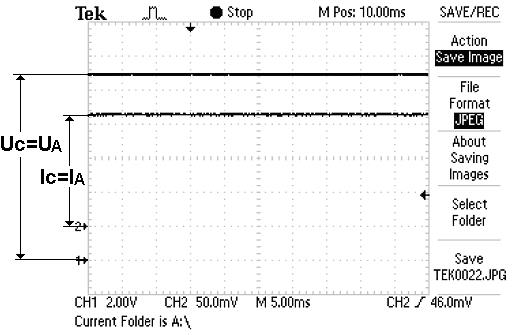
Рис. 31. Осциллограмма напряжения и тока на клеммах аккумулятора и лампочки
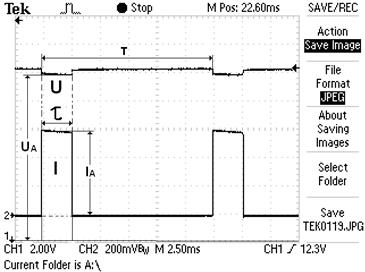
Рис. 32. Осциллограмма импульсной разрядки аккумулятора
Если же напряжение и ток потребляются импульсами с длительностью (например, 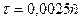 рис. 32) значительно меньшей длительности секунды, то мощность, определённая произведением амплитуд импульсов напряжения
рис. 32) значительно меньшей длительности секунды, то мощность, определённая произведением амплитуд импульсов напряжения 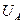 и тока
и тока 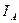 , не соответствует понятию Ватт, введённому в систему СИ, которая требует их непрерывного действия в интервале длительности всей секунды. Чтобы результат перемножения импульсных значений напряжения и тока соответствовал понятию Ватт, надо действие напряжения и тока растянуть до длительности одной секунды (рис. 32). Для реализации этой операции, давно введено понятие «скважность импульсов». Если импульсы напряжения и тока прямоугольные (рис. 32), то их скважность
, не соответствует понятию Ватт, введённому в систему СИ, которая требует их непрерывного действия в интервале длительности всей секунды. Чтобы результат перемножения импульсных значений напряжения и тока соответствовал понятию Ватт, надо действие напряжения и тока растянуть до длительности одной секунды (рис. 32). Для реализации этой операции, давно введено понятие «скважность импульсов». Если импульсы напряжения и тока прямоугольные (рис. 32), то их скважность 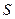 равна отношению периода
равна отношению периода 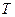 следования импульсов к длительности
следования импульсов к длительности 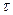 импульса (рис. 32).
импульса (рис. 32).
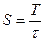 . (28)
. (28)
Если импульсы имеют сложную форму, то их скважность определяется отношением площади осциллограммы, ограниченной по горизонтали длительностью периода 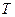 (рис. 32), а по вертикали – амплитудой импульсов напряжения
(рис. 32), а по вертикали – амплитудой импульсов напряжения 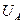 или тока
или тока 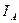 к площади, занимаемой этими импульсами в указанных границах. При этом скважность импульсов напряжения
к площади, занимаемой этими импульсами в указанных границах. При этом скважность импульсов напряжения 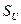 может отличаться от скважности импульсов тока
может отличаться от скважности импульсов тока 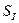 . Тогда средние величины напряжения
. Тогда средние величины напряжения 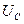 и тока
и тока 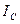 , соответствующие понятию Ватт, определяются по формулам:
, соответствующие понятию Ватт, определяются по формулам:
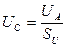 ; (29)
; (29)
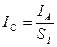 . (30)
. (30)
Из этого следует, что средняя импульсная мощность 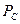 , соответствующая понятию Ватт, определится по формуле
, соответствующая понятию Ватт, определится по формуле
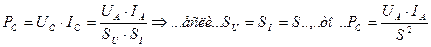 . (31)
. (31)
Проверяем физическое соответствие этой формулы системе СИ. Наличие скважности импульсов тока 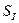 , подтверждает то, что величина амплитуды тока
, подтверждает то, что величина амплитуды тока 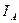 растянута до значения, соответствующего непрерывному её действию в течение всего периода
растянута до значения, соответствующего непрерывному её действию в течение всего периода 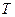 . Далее, появление импульсов тока (рис. 32) с амплитудами
. Далее, появление импульсов тока (рис. 32) с амплитудами 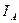 автоматически формирует импульсы напряжения с амплитудами
автоматически формирует импульсы напряжения с амплитудами 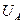 и длительностью
и длительностью 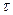 , соответствующей длительности импульсов тока (рис. 32). Чтобы указанные импульсы напряжения также соответствовали системе СИ, их тоже надо растянуть до длительности периода
, соответствующей длительности импульсов тока (рис. 32). Чтобы указанные импульсы напряжения также соответствовали системе СИ, их тоже надо растянуть до длительности периода 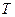 , то есть разделить амплитудные значения напряжения
, то есть разделить амплитудные значения напряжения 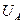 на скважность их импульсов
на скважность их импульсов 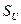 . Описанное чётко отражено в формуле (31). Значит, она точно отражает физический смысл, заложенный системой СИ в понятие Ватт.
. Описанное чётко отражено в формуле (31). Значит, она точно отражает физический смысл, заложенный системой СИ в понятие Ватт.
Однако, в учебниках по электротехнике уже более 100 лет написано, что средняя импульсная мощность 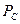 рассчитывается путём деления произведения амплитудных значений напряжения
рассчитывается путём деления произведения амплитудных значений напряжения 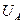 и тока
и тока 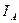 (рис. 32) на скважность импульсов
(рис. 32) на скважность импульсов 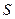 один раз
один раз
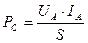 . (32)
. (32)
Чтобы понять физику процесса превращения интегральной формулы (24) в формулу (32), внимательно проанализируем процесс графического интегрирования функций напряжения 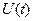 и тока
и тока 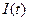 , представленных в интегральной формуле (24). Это необходимо для проверки соответствия этой формулы системе СИ и для проверки правильного перевода электрической энергии в другие виды энергии, например, в тепловую. Чтобы проверка была наглядной, привяжем её к осциллограмме, снятой с клемм аккумулятора, к которому подключена лампочка, потребляющая энергию импульсами тока с амплитудами
, представленных в интегральной формуле (24). Это необходимо для проверки соответствия этой формулы системе СИ и для проверки правильного перевода электрической энергии в другие виды энергии, например, в тепловую. Чтобы проверка была наглядной, привяжем её к осциллограмме, снятой с клемм аккумулятора, к которому подключена лампочка, потребляющая энергию импульсами тока с амплитудами 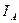 , и импульсами напряжения с амплитудами
, и импульсами напряжения с амплитудами 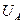 (рис. 32). Когда импульс тока исчезает, то напряжение на клеммах аккумулятора восстанавливается до прежней величины, и оно не участвует в формировании мощности, отбираемой у аккумулятора, до появления следующего импульса тока. Это неучастие реализуется математической формулой (24) следующим образом. При графическом интегрировании она перемножает мгновенные значения напряжения и тока. На рис. 32 хорошо видно, что в интервале длительности импульса
(рис. 32). Когда импульс тока исчезает, то напряжение на клеммах аккумулятора восстанавливается до прежней величины, и оно не участвует в формировании мощности, отбираемой у аккумулятора, до появления следующего импульса тока. Это неучастие реализуется математической формулой (24) следующим образом. При графическом интегрировании она перемножает мгновенные значения напряжения и тока. На рис. 32 хорошо видно, что в интервале длительности импульса 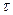 , указанное перемножение амплитудных значений напряжения и тока даёт средний результат
, указанное перемножение амплитудных значений напряжения и тока даёт средний результат 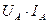 . Когда действие импульса тока заканчивается, то его величина становится равной нулю. Это автоматически останавливает участие импульса напряжения с амплитудой
. Когда действие импульса тока заканчивается, то его величина становится равной нулю. Это автоматически останавливает участие импульса напряжения с амплитудой 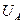 в формировании средней величины мощности
в формировании средней величины мощности 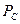 . Математики считают, что неучастие напряжения в формировании средней величины импульсной мощности в интервале
. Математики считают, что неучастие напряжения в формировании средней величины импульсной мощности в интервале 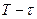 реализуется тем, что произведение нулевых значений тока
реализуется тем, что произведение нулевых значений тока 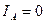 , в указанном интервале, на амплитудные значения напряжения
, в указанном интервале, на амплитудные значения напряжения 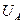 даёт нулевое значение средней мощности
даёт нулевое значение средней мощности 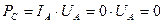 . Логичность такого математического результата убедительна. А как при этом реализуется физическая суть процесса формирования средней импульсной мощности, соответствующей понятию Ватт? Мы не знаем почему, но поиск ответа на этот вопрос достался только нам. Вот физическая суть этого ответа.
. Логичность такого математического результата убедительна. А как при этом реализуется физическая суть процесса формирования средней импульсной мощности, соответствующей понятию Ватт? Мы не знаем почему, но поиск ответа на этот вопрос достался только нам. Вот физическая суть этого ответа.
Мы уже знаем, что величины импульсов напряжения и тока будут соответствовать понятию Ватт, введённому в систему СИ, только в том случае, когда их действие растянуто до длительности всего периода 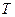 . Электронная программа, заложенная в осциллограф, автоматически считает все ординаты произведений мгновенных значений напряжений и токов, в том числе и - равные нулю. Так как этот процесс осуществляется в интервале времени
. Электронная программа, заложенная в осциллограф, автоматически считает все ординаты произведений мгновенных значений напряжений и токов, в том числе и - равные нулю. Так как этот процесс осуществляется в интервале времени 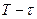 равенства нулю только тока, то он эквивалентен делению произведений амплитудных значений напряжений и токов на скважность импульсов
равенства нулю только тока, то он эквивалентен делению произведений амплитудных значений напряжений и токов на скважность импульсов 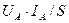 и формула (24) превращается, в упрощённую формулу, показанную в конце выражения (33).
и формула (24) превращается, в упрощённую формулу, показанную в конце выражения (33).
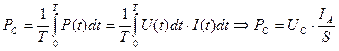 . (33)
. (33)
Нетрудно установить каким импульсам: напряжения или тока принадлежит скважность 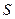 в формуле (33). Так как в интервале времени
в формуле (33). Так как в интервале времени 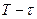 нулевые значения принимает только ток, то скважность, входящая в формулу (33), принадлежит только току, а напряжение вошло в эту формулу полной своей средней величиной, определённой не в интервале всего периода
нулевые значения принимает только ток, то скважность, входящая в формулу (33), принадлежит только току, а напряжение вошло в эту формулу полной своей средней величиной, определённой не в интервале всего периода 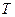 , а в интервале
, а в интервале 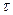 только длительности импульса напряжения. Из этого автоматически следует, что величина среднего напряжения
только длительности импульса напряжения. Из этого автоматически следует, что величина среднего напряжения 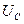 вошла в формулу (33) в нерастянутом состоянии, то есть без деления на скважность её импульса, которая учитывала бы не математическое, а физическое неучастие напряжения в формировании средней величины мощности в интервале
вошла в формулу (33) в нерастянутом состоянии, то есть без деления на скважность её импульса, которая учитывала бы не математическое, а физическое неучастие напряжения в формировании средней величины мощности в интервале 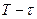 . За счёт этой величина средней мощности
. За счёт этой величина средней мощности 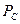 , оказывается увеличенной в количество раз, равное скважности импульсов
, оказывается увеличенной в количество раз, равное скважности импульсов 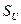 напряжения.
напряжения.
Таким образом, мы установили владельца скважности 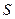 , вошедшей в формулу (33). Она
, вошедшей в формулу (33). Она 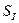 принадлежит импульсу тока
принадлежит импульсу тока 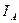 и мы обязаны указать это в формуле (33) и записать её так
и мы обязаны указать это в формуле (33) и записать её так
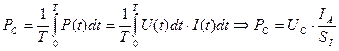 . (34)
. (34)
Наличие в формуле (33) скважности 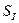 импульсов тока
импульсов тока 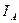 означает, что его амплитудное значение растянуто до длительности периода
означает, что его амплитудное значение растянуто до длительности периода 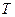 , что полностью соответствует понятию Ватт. Отсутствие скважности
, что полностью соответствует понятию Ватт. Отсутствие скважности 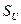 импульсов напряжения
импульсов напряжения 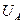 в формуле (33) автоматически означает, что величина
в формуле (33) автоматически означает, что величина 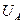 осталась не растянутой до длительности всего периода
осталась не растянутой до длительности всего периода 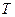 и участвует в формировании мощности всей своей величиной
и участвует в формировании мощности всей своей величиной 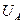 в течение всего периода, что искажает конечный результат в количество раз, равное скважности импульсов
в течение всего периода, что искажает конечный результат в количество раз, равное скважности импульсов 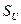 напряжения. Это и есть фундаментальная физическая ошибка математиков, которая оставалась незамеченной более 100 лет.
напряжения. Это и есть фундаментальная физическая ошибка математиков, которая оставалась незамеченной более 100 лет.
Вновь обращаемся к рис. 32 и видим, что напряжение участвовало в формировании мощности только в интервале длительности импульса 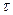 и не участвовало в интервале
и не участвовало в интервале 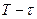 , поэтому мы обязаны растянуть амплитуду (
, поэтому мы обязаны растянуть амплитуду ( 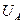 ) его действия на весь интервал
) его действия на весь интервал 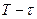 . Делается это путём деления величины
. Делается это путём деления величины 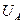 на скважность импульсов. Отсутствие этой операции в математической модели (33) автоматически делает величину средней мощности
на скважность импульсов. Отсутствие этой операции в математической модели (33) автоматически делает величину средней мощности 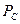 не соответствующей понятию Ватт, введённому в систему СИ, в количество раз равное скважности импульсов напряжения
не соответствующей понятию Ватт, введённому в систему СИ, в количество раз равное скважности импульсов напряжения 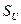 .
.
Так что существующий процесс учета электроэнергии, основанный на математической модели (33) – произволен и противоречит понятию Ватт, заложенному в систему СИ. Он даёт не Ватты, а винегрет из электрических величин. Все электросчётчики увеличивают величину потребляемой импульсной электрической энергии в количество раз, равное скважности импульсов напряжения. Это колоссальный энергетический резерв, остававшийся незамеченным более 100 лет. Наша задача доказать экспериментально наличие этого резерва. Реализация этого намерения длилась более 10 лет, так как все специалисты, с которыми приходилось обсуждать эту проблему, яростно доказывали правильность математической модели (33) для расчёта средней величины импульсной мощности и правильность показаний счётчиков электроэнергии, в которых реализуется эта модель.
Для доказательства достоверности математической модели (31) расчёта средней импульсной мощности проанализируем баланс мощности электромотора – генератора МГ-2, который потребляет энергию из аккумулятора импульсами напрямую, без каких либо промежуточных электронных устройств (рис. 33). Роль мотора у него выполняет ротор, а роль генератора – статор.
В качестве нагрузки возьмём ячейку электролизёра (рис. 34), проследим за процессом разрядки мотоциклетного аккумулятора 6МТС-9, питающего электромотор – генератор, и сравним с процессом разрядки такого же аккумулятора, питающего совокупность лампочек с общей мощностью, равной мощности, отбираемой у аккумулятора электромотором – генератором, рассчитанной по старой математической модели (32).

Рис. 33. Мотор-генератор МГ-2 и мотоциклетный аккумулятор для его питания

Рис. 34. Фото МГ-2 + 2 аккумулятора 6МТС-9 + ячейка электролизёра
Осциллограммы, снятые с клемм Мг-2 и аккумулятора, представлены на рис. 35 и 36. Значения напряжения и мощности, рассчитанные по старой математической модели (32), обозначены символами 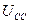 и
и 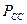 , а по - новой - (31) -
, а по - новой - (31) - 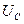 и
и 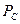 .
.
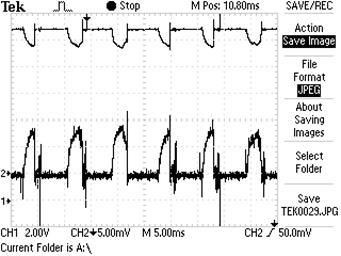
| Холостой ход МГ-2.
Показания осциллографа
на клеммах ротора МГ-2:
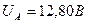 ; ;
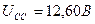 ; ;
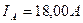 ; ;
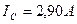 .
Результаты расчёта: .
Результаты расчёта:
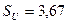 ; ; 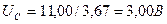 ; ;
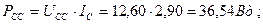
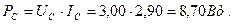
|
Рис. 35. Осциллограмма холостого хода ротора Мг-2
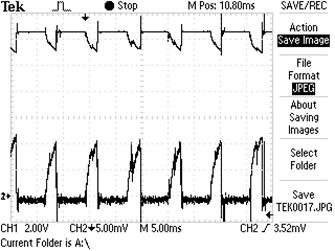
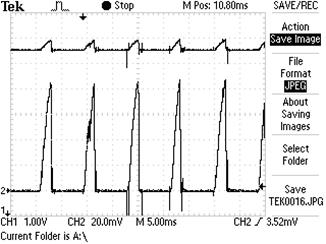
МГ-2 работал в режиме поочерёдной разрядки и зарядки аккумуляторов, как автономный источник энергии. Осциллограммы на 100 – й минуте опыта, длившегося 3 часа 10 мин. 2 представлены на рис. 36. Частота - 1800об/мин. Осциллограммы на клеммах ротора и статора МГ-2.
Итак, электронная программа осциллографа (рис. 35 и 36), определяющая средние значения напряжения и тока, базируется на математической модели (32). Справа осциллограмм (рис. 35 и 36) представлены средние значения напряжения 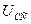 и мощности
и мощности 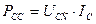 , рассчитанные по старой математической модели (32). Для расчёта величин нового среднего напряжения
, рассчитанные по старой математической модели (32). Для расчёта величин нового среднего напряжения 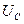 использовалась новая математическая модель (31), а для расчёта нового среднего значения импульсной электрической мощности – математическая модель (31) нового закона формирования средней величины импульсной электрической мощности. Результаты расчётов, следующие из осциллограмм (рис. 35 и 36) представляем в таблицах 2 и 3.
использовалась новая математическая модель (31), а для расчёта нового среднего значения импульсной электрической мощности – математическая модель (31) нового закона формирования средней величины импульсной электрической мощности. Результаты расчётов, следующие из осциллограмм (рис. 35 и 36) представляем в таблицах 2 и 3.
На РОТОРЕ –рабочий ход
| Ток прибора, 2,80А;
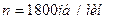 .
Осциллограф: .
Осциллограф:
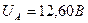 ; ;
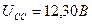 ; ;
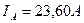 ; ;
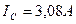 ; ;
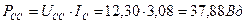 .
Расчётные данные: .
Расчётные данные:
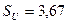 ; ; 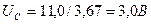 ; ;
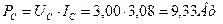 . .
|
На СТАТОРЕ +1 ячейка
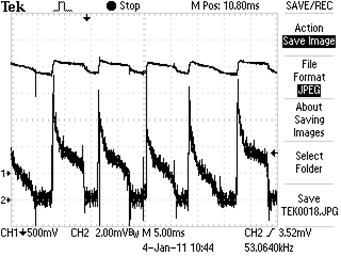
| Осциллограф:
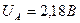 ; ;
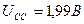 ; ;
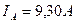 ; ;
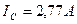 ; ;
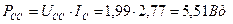 .
Расход раствора - ∆m=4,6 г,
8,57л или 2,7 л/час ( .
Расход раствора - ∆m=4,6 г,
8,57л или 2,7 л/час ( 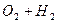 ).
Расчётные данные: ).
Расчётные данные:
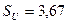 ; ; 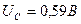 ; ;
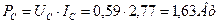 ; ;
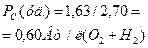 . .
|
На СТАТОРЕ + зарядка аккумуляторов
| Осциллограф:
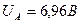 ; ;
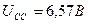 ; ;
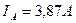 ; ;
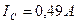 ; ;
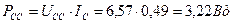 .
Расчётные данные: .
Расчётные данные:
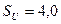 ; ; 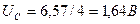 ; ;
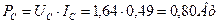 . .
|
Рис. 36. Осциллограммы электромотора-генератора МГ-2 на 100 – й минуте эксперимента
Таблица 2. Старые 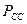 и новые
и новые 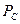 средние импульсные мощности
средние импульсные мощности
на клеммах ротора и статора МГ-2
| Мощность на клеммах: | Старая мощность, 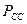 Вт Вт
| Новая мощность, 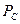 Вт Вт
|
| 1. Ротора (хол. ход) | 36,54 | 8,70 |
| 2. Ротор (рабочий ход) | 37,88 | 9,33 |
| 3. Статор (ЭДС самоиндукции) | 5,51 | 1,63 |
| 4. Статор (ЭДС индукции) | 3,22 | 0,80 |
Дата добавления: 2016-02-02; просмотров: 1087;
