Теоретическая часть. Мотор-генератор МГ-1 имеет обычный ротор и обычный статор
Мотор-генератор МГ-1 имеет обычный ротор и обычный статор. Роль мотора у него выполняет ротор, а роль генератора - статор (рис. 38). Потребовалось около 100 лет, чтобы понять, как заставить ротор генератора вращаться без постороннего привода.
Теоретический баланс мощности МГ-1 на холостом ходу представлен на рис. 39, а экспериментальный пусковой – на рис. 40.

Рис. 38. Фото мотора-генератора МГ-1
В момент начала вращения ротора его пусковой момент 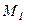 преодолевает сопротивления в виде моментов механических и рабочих сопротивлений
преодолевает сопротивления в виде моментов механических и рабочих сопротивлений 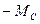 и в виде инерциального момента
и в виде инерциального момента 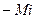 . Сумма этих сопротивлений равна
. Сумма этих сопротивлений равна 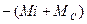 (рис. 39).
(рис. 39).
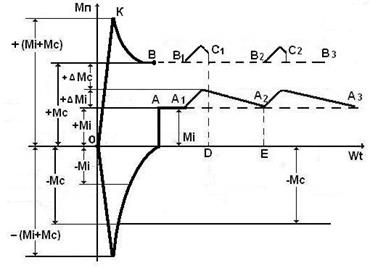
Рис. 39. График изменения вращающих моментов, действующих на ротор МГ-1
при запуске его в работу, и при равномерном вращении
Анализ осциллограммы на рис. 40, показывает, что величины амплитуд импульсов тока становятся одинаковыми, примерно, после 5-го импульса. Это значит, что равномерное вращение ротора начинается после 5-го импульса. На рис. 39 момент, когда инерциальный момент становится положительным 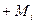 , соответствует точке В. Амплитуда первого импульса напряжения - 100В, а амплитуда первого импульса тока (рис. 40) - 10А. Это значит, что мощность пускового импульса равна 100х10=1000Вт. (Особо подчеркнём мгновенного пускового, а не средний пусковой). Она реализуется на преодоление инерциального момента
, соответствует точке В. Амплитуда первого импульса напряжения - 100В, а амплитуда первого импульса тока (рис. 40) - 10А. Это значит, что мощность пускового импульса равна 100х10=1000Вт. (Особо подчеркнём мгновенного пускового, а не средний пусковой). Она реализуется на преодоление инерциального момента 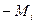 и забирается у первичного источника энергии один раз, в момент пуска ротора в работу, и поэтому не учитывается в балансе мощности МГ-1, которая реализуется в течение многих часов его работы.
и забирается у первичного источника энергии один раз, в момент пуска ротора в работу, и поэтому не учитывается в балансе мощности МГ-1, которая реализуется в течение многих часов его работы.
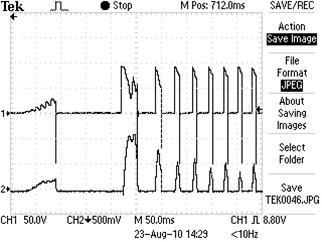
Рис. 40. Осциллограмма пусковых значений напряжения и тока
обмотки возбуждения ротора без маховика
Поскольку инерциальный момент ротора участвует в процессе его пуска, то надо знать его величину. Для этого надо, прежде всего, определить кинетическую энергию равномерно вращающегося ротора и механическую мощность на его валу при этом вращении, используя формулу (40).
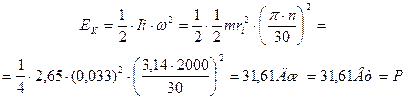 . (35)
. (35)
Инерциальный момент 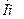 , генерирующий кинетическую энергию (35) равномерно вращающегося ротора, равен
, генерирующий кинетическую энергию (35) равномерно вращающегося ротора, равен
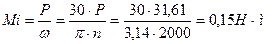 . (36)
. (36)
Мы вычислили величину мощности (35) на валу равномерно вращающегося ротора и инерциальный момент (36), сопровождающий это вращение и не признаваемый динамикой Ньютона. Таким образом, на валу равномерно вращающегося ротора МГ-1, с 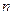 = 2000об/мин. постоянно присутствует механическая мощность, равная 31,61 Вт (35) и инерциальный момент, генерирующий эту мощность, равный
= 2000об/мин. постоянно присутствует механическая мощность, равная 31,61 Вт (35) и инерциальный момент, генерирующий эту мощность, равный 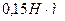 (36).
(36).
Ошибочность формулы (32), как мы уже показали, обусловлена тем, что и при генерировании импульсной мощности и при её потреблении импульсы тока, всегда рождают импульсы напряжения. Это автоматически требует деления на скважность импульсов не только тока, но и напряжения, что и отражено в формуле (31). Таким образом, если в электрическую цепь потребления подаются импульсы напряжения, то формула (32) искажает результат, так как однократное деление произведения амплитудных значений 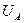 и
и 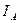 на скважность импульсов
на скважность импульсов 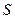 превращает одну из них в непрерывную величину, что явно противоречит реальности, отображённой на рис. 41, где напряжение и ток – величины импульсные.
превращает одну из них в непрерывную величину, что явно противоречит реальности, отображённой на рис. 41, где напряжение и ток – величины импульсные.
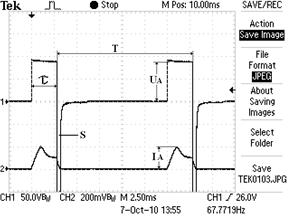 Рис. 41. Импульсы напряжения и тока в
обмотке ротора на холостом ходу
Рис. 41. Импульсы напряжения и тока в
обмотке ротора на холостом ходу
| 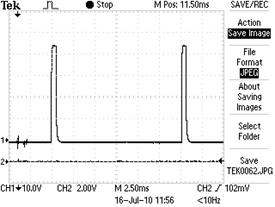 Рис. 42. Импульсы ЭДС самоиндукции в обмотке статора на холостом ходу
Рис. 42. Импульсы ЭДС самоиндукции в обмотке статора на холостом ходу
|
Напряжение от первичного источника питания подаётся в обмотку возбуждения ротора МГ-1 (рис. 41). Амплитуды импульсов напряжения равны 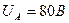 , а их скважность -
, а их скважность - 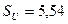 . Если импульсы тока привести к прямоугольной форме, то скважности импульсов напряжения и тока будут равны
. Если импульсы тока привести к прямоугольной форме, то скважности импульсов напряжения и тока будут равны 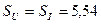 . Тогда величина амплитуды тока будет равна
. Тогда величина амплитуды тока будет равна 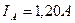 . С учётом этого средние значения импульсов напряжения и тока будут равны:
. С учётом этого средние значения импульсов напряжения и тока будут равны:
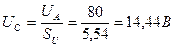 ; (37)
; (37)
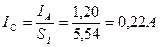 , (38)
, (38)
а средняя электрическая мощность холостого хода на валу ротора (рис. 41) оказывается такой
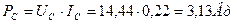 . (39)
. (39)
А теперь разберёмся с физическим смыслом средней импульсной мощности, представленной в формуле (39). На рис. 39 положительный 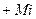 инерциальный момент, соответствует механической энергии (мощности) равномерно вращающегося ротора. Мощность, соответствующая этому моменту, равна 31,61 Вт (35). Эта мощность присутствует на валу ротора постоянно при его равномерном вращении. Когда в обмотку ротора подаются импульсы напряжения с амплитудой
инерциальный момент, соответствует механической энергии (мощности) равномерно вращающегося ротора. Мощность, соответствующая этому моменту, равна 31,61 Вт (35). Эта мощность присутствует на валу ротора постоянно при его равномерном вращении. Когда в обмотку ротора подаются импульсы напряжения с амплитудой 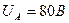 , то одновременно формируется импульс тока с амплитудой
, то одновременно формируется импульс тока с амплитудой 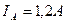 (рис. 41). Средние значения этих импульсов равны:
(рис. 41). Средние значения этих импульсов равны: 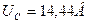 (37),
(37), 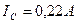 (38), а их средняя электрическая мощность равна 3,13 Ватта (39). Это реальная электрическая мощность импульсов, поданных от первичного источника энергии в обмотку возбуждения ротора. Она складывается с величиной инерциальной механической мощности 31,61 Ватта (35), постоянно присутствующей на его валу при равномерном вращении ротора (рис. 41, 42). Суммарная импульсная мощность на валу ротора, в момент подачи в его обмотку импульса напряжения от первичного источника питания, равна
(38), а их средняя электрическая мощность равна 3,13 Ватта (39). Это реальная электрическая мощность импульсов, поданных от первичного источника энергии в обмотку возбуждения ротора. Она складывается с величиной инерциальной механической мощности 31,61 Ватта (35), постоянно присутствующей на его валу при равномерном вращении ротора (рис. 41, 42). Суммарная импульсная мощность на валу ротора, в момент подачи в его обмотку импульса напряжения от первичного источника питания, равна
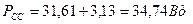 (40).
(40).
В результате этого постоянный инерциальный момент 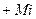 получает импульсную прибавку
получает импульсную прибавку 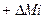 (рис. 39), величина которой соответствует импульсу электрической мощности
(рис. 39), величина которой соответствует импульсу электрической мощности 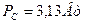 (39). Эта прибавка идёт на преодоление сопротивлений
(39). Эта прибавка идёт на преодоление сопротивлений 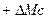 , которые формируются процессами генерации напряжения и тока в обмотке возбуждения ротора в моменты, когда его электрическая цепь замкнута (рис. 39, интервалы
, которые формируются процессами генерации напряжения и тока в обмотке возбуждения ротора в моменты, когда его электрическая цепь замкнута (рис. 39, интервалы 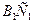 и
и 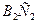 ). Как только электрическая цепь ротора размыкается, то сопротивления формирующиеся импульсами электрической мощности, рождающей импульсы инерциальных
). Как только электрическая цепь ротора размыкается, то сопротивления формирующиеся импульсами электрической мощности, рождающей импульсы инерциальных 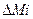 прибавок к инерциальному моменту
прибавок к инерциальному моменту 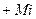 , исчезают (рис. 39, интервал
, исчезают (рис. 39, интервал 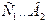 или D…E), а оставшийся запас инерциального момента
или D…E), а оставшийся запас инерциального момента 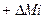 продолжает вращать ротор до получения им следующего импульса (рис. 39, точка
продолжает вращать ротор до получения им следующего импульса (рис. 39, точка 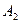 ). Из этого следует, что ротор забирает из сети импульсы электрической энергии. Их средняя мощность равна 3,13 Ватта (39). Из этого следует закон формирования мощности в электрической цепи. Он гласит: средняя мощность в любом сечении электрической цепи равна произведению средних значений напряжения и тока (39) [1].
). Из этого следует, что ротор забирает из сети импульсы электрической энергии. Их средняя мощность равна 3,13 Ватта (39). Из этого следует закон формирования мощности в электрической цепи. Он гласит: средняя мощность в любом сечении электрической цепи равна произведению средних значений напряжения и тока (39) [1].
Мы рассмотрели процесс пуска ротора МГ-1 и процесс его равномерного вращения и нас удивляет мизерная величина электрической мощности 3,13 Вт (39), которая вращает равномерно ротор с массой 2,6 кг и частотой 2000 об./мин на холостом ходу. Это удивление – следствие не учета нашим воображением 31,61Вт мощности, постоянно присутствующей на валу ротора МГ-1 при его равномерном вращении. Этот не учёт сформирован ошибочным первым законом Ньютона. Надо понимать, что мощность 3,13 Вт реализуется только на генерацию импульсов напряжения и тока в обмотке возбуждения ротора, которые формируют импульсные механические инерциальные прибавки 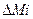 к инерциальному моменту
к инерциальному моменту 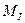 , преодолевающему все механические сопротивления.
, преодолевающему все механические сопротивления.
Таким образом, постоянно присутствующая механическая мощность 31,61 Вт на валу ротора преодолевает все виды постоянных сопротивлений его вращению, а импульсы электрической мощности 3,13Вт (рис. 39, интервалы 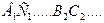 .), формируя импульсы магнитных моментов при взаимодействии магнитных полюсов ротора и статора, генерируют импульсные инерциальные прибавки
.), формируя импульсы магнитных моментов при взаимодействии магнитных полюсов ротора и статора, генерируют импульсные инерциальные прибавки 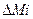 инерциальному моменту
инерциальному моменту 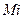 и одновременно формируют рабочие импульсы ЭДС индукции и ЭДС самоиндукции в обмотке статора [1].Это очень экономный процесс одновременного генерирования электрических и механических импульсов мощности.
и одновременно формируют рабочие импульсы ЭДС индукции и ЭДС самоиндукции в обмотке статора [1].Это очень экономный процесс одновременного генерирования электрических и механических импульсов мощности.
А теперь обратим внимание на узкий импульс S (рис. 41) ЭДС самоиндукции, возникающий в обмотке возбуждения ротора после формирования импульса ЭДС индукции. В обмотке статора также генерируются импульсы ЭДС индукции и ЭДС самоиндукции (рис. 42).
3.2. МГ + ячейка электролизёра + лампочка
Следующий этап - анализ баланса мощности МГ-1, ячейки электролизёра, включённого в цепь ЭДС самоиндукции статора и лампочки, включённой в цепь ЭДС индукции статора(рис. 43, а). Осциллограммы напряжения и тока в обмотке возбуждения ротора, генерирующего мощность для питания одной ячейки электролизёра, подключённой в цепь ЭДС самоиндукции статора, и одной лампочки, подключённой в цепь ЭДС индукции статора, представлены на рис. 43, b, c и d.
Чтобы упростить расчёт мощности на валу ротора, приведём импульс тока (рис. 43, b) к прямоугольной форме. Тогда обработка осциллограммы даёт одинаковые величины скважности импульсов напряжения и тока, равные 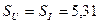 . С учётом этого средняя величина напряжения равна
. С учётом этого средняя величина напряжения равна
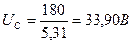 , (41)
, (41)
а тока
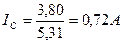 . (42)
. (42)
Тогда средняя электрическая мощность на валу ротора равна
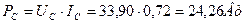 . (43)
. (43)
Известно, что электролиз воды идёт при среднем напряжении на каждую ячейку, равном, примерно, 2 Вольта. Почему? Неизвестно. Неизвестно и влияние количества ячеек на производительность электролизёра. Ответ на этот вопрос получен недавно, при использовании самовращающегося генератора МГ-1 для питания электролизёра. Он выдаёт импульсы напряжения, которые не имеют прямой связи с первичным источником питания: аккумулятором или электрической сетью. Амплитуда и частота импульсов напряжения, которые он выдаёт, тесно связаны с его конструкцией и определяются частотой его вращения.
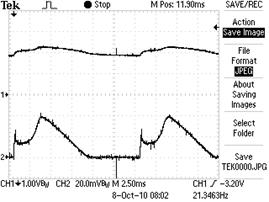
На рис. 42 представлена осциллограмма импульсов ЭДС самоиндукции, генерируемых в обмотке статора МГ-1 на холостом ходу, в момент разрыва электрической цепи, питающей обмотку ротора. Амплитуда импульсов напряжения равна 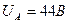 (рис. 42), длительность импульсов – 0,50мс, а их скважность равна S=21,50 при оборотах ротора генератора, равных 2000 об./мин. Средняя величина ЭДС самоиндукции, генерируемая в обмотке статора равна, Uc=44/21,50=2,05B. На рис. 43, с – эти же импульсы (рис. 42), трансформированные одной ячейкой классического электролизёра.
(рис. 42), длительность импульсов – 0,50мс, а их скважность равна S=21,50 при оборотах ротора генератора, равных 2000 об./мин. Средняя величина ЭДС самоиндукции, генерируемая в обмотке статора равна, Uc=44/21,50=2,05B. На рис. 43, с – эти же импульсы (рис. 42), трансформированные одной ячейкой классического электролизёра.
Следующий этап – расчёт мощности, реализуемой на работу ячейки электролизёра. Как видно (рис. 43, с), ячейка уменьшает амплитуду импульса с 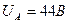 до, примерно,
до, примерно, 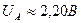 , то есть в количество раз, равное скважности импульсов (S=21,51) напряжения на холостом ходу генератора (рис. 42).
, то есть в количество раз, равное скважности импульсов (S=21,51) напряжения на холостом ходу генератора (рис. 42).
Чтобы упростить расчёт, приводим импульсы тока (рис. 43, c) к прямоугольной форме. Тогда скважности импульсов напряжения и тока будут равны 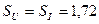 , а амплитуда тока
, а амплитуда тока 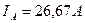 . С учетом этого среднее напряжение, подаваемое в ячейку, будет равно
. С учетом этого среднее напряжение, подаваемое в ячейку, будет равно
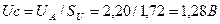 . (44)
. (44)
Обратим внимание на то, что среднее напряжение импульса 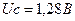 , меньше среднего напряжения (рис. 43, c около 2-х Вольт) на клеммах ячейки. Обусловлено это тем, что ячейка, зарядившись вначале, постепенно разряжается, а подаваемые импульсы напряжения с амплитудой 2,20 В и со скважностью S=1,72, подзаряжают её. При этом скважность S=1,72 уменьшает амплитуду импульса напряжения
, меньше среднего напряжения (рис. 43, c около 2-х Вольт) на клеммах ячейки. Обусловлено это тем, что ячейка, зарядившись вначале, постепенно разряжается, а подаваемые импульсы напряжения с амплитудой 2,20 В и со скважностью S=1,72, подзаряжают её. При этом скважность S=1,72 уменьшает амплитуду импульса напряжения 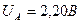 до средней величины 1,28В, используемой для расчёта мощности. Очень важно понять этот момент. Величина 2,20 В принадлежит электролизёру, а не источнику питания. Источнику питания (ЭДС самоиндукции статора) принадлежит средняя величина напряжения 1,28В.
до средней величины 1,28В, используемой для расчёта мощности. Очень важно понять этот момент. Величина 2,20 В принадлежит электролизёру, а не источнику питания. Источнику питания (ЭДС самоиндукции статора) принадлежит средняя величина напряжения 1,28В.
 а) МГ-1, электролизёр и лампочка
а) МГ-1, электролизёр и лампочка
| 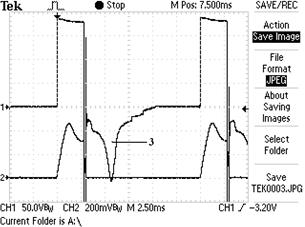 b) напряжение и ток на щётках ротора
b) напряжение и ток на щётках ротора
|
 с) напряжение и ток на клеммах
электролизёра
с) напряжение и ток на клеммах
электролизёра
|  d) напряжение и ток на клеммах
лампочки
d) напряжение и ток на клеммах
лампочки
|
Рис. 43. МГ-1 и его потребители: электролизёр и лампочка
Средняя величина тока равна
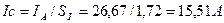 , (45)
, (45)
а мощности –
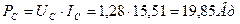 . (46)
. (46)
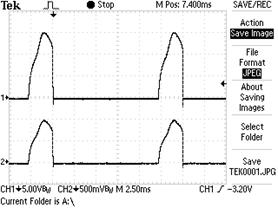
Теперь определим мощность на клеммах лампочки c номинальной мощностью 20Вт, подключённой в цепь ЭДС индукции статора. Осциллограмма импульсов напряжения и тока на клеммах этой лампочки представлена на рис. 43, d. Приводим импульсы напряжения и тока к прямоугольной форме. Тогда их скважность будет равна 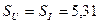 . Амплитуда напряжения равна
. Амплитуда напряжения равна 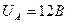 , а тока
, а тока 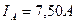 . Средние значения напряжения и тока будут равны:
. Средние значения напряжения и тока будут равны:
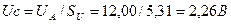 ; (47)
; (47)
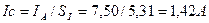 , (48)
, (48)
Обратим внимание на то, что в цепи ЭДС индукции статора напряжение генерируется не постоянное, а импульсное (рис. 43, d), поэтому мы обязаны рассчитывать мощность на клеммах лампочки по формуле (46). В результате будем иметь
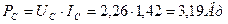 . (49)
. (49)
Однако, лампочка, включённая в цепь ЭДС индукции статора в паре с ячейкой электролизёра, включённой в цепь ЭДС самоиндукции статора, имела полный накал, соответствующий её номинальной мощности 20Вт. Из этого следует, что полная мощность в обмотке статора равнялась
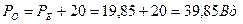 . (50)
. (50)
Разделим мощность в обмотке статора (50) на мощность в обмотке ротора (43).
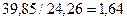 (51)
(51)
Таким образом, мощность, генерируемая в обмотке статора (50), в 1,64 (51) раза больше мощности в обмотке ротора (43). Для проверки достоверности этой эффективности МГ-1 был проведён контрольный эксперимент.
Дата добавления: 2016-02-02; просмотров: 1808;
