УРАВНЕНИЕ ПЬЕЗОПРОВОДНОСТИ

Математической основой для анализа ГДИС на неустановившихся режимах фильтрации является уравнение пьезопроводности в радиальных координатах, описывающее неустановившееся, однофазное, одномерное течение флюида в пористой среде.

Вывод уравнения пьезопроводности основывается на трех законах (рис. 1.5.1): Уравнение неразрывности (закон сохранения массы);

Закон Дарси;

Уравнение состояния .

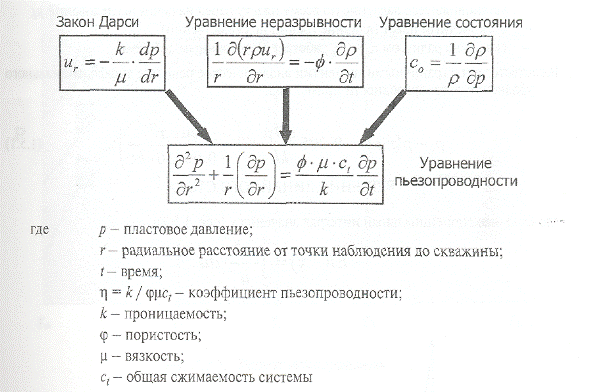
Рис. 1.5.1. Вывод уравнения пьезопроводности

Условные допущения, используемые при выводе уравнения:

· радиальный режим притока по всей эффективной толщине пласта;

· однородный, изотропный пласт (k_x = k_y - k_z);

· эффективная толщина пласта постоянна;

· q и k - постоянны (не зависят от давления);

· сжимаемость жидкости мала и постоянна;

· вязкость 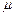постоянна;

· маленький градиент давления

· гравитационные силы пренебрежимо малы.

Уравнение пьезопроводности выражает связь между пластовым давлением, временем и расстоянием от скважины до точки наблюдения. Если наложить граничные условия-

· начальное давление,

· границы пласта,

· скважина.

то можно решить уравнение и получить модель, характеризующую перераспределение давления в пласте.

При решении уравнения пьезопроводности обычно накладываются следующие граничные условия:

· установившееся давление по всему пласту перед началом исследований

p_i

· бесконечный пласт (влияние границ не существенно)

· скважина радиусом r_w « r_e работает с постоянным дебитом.

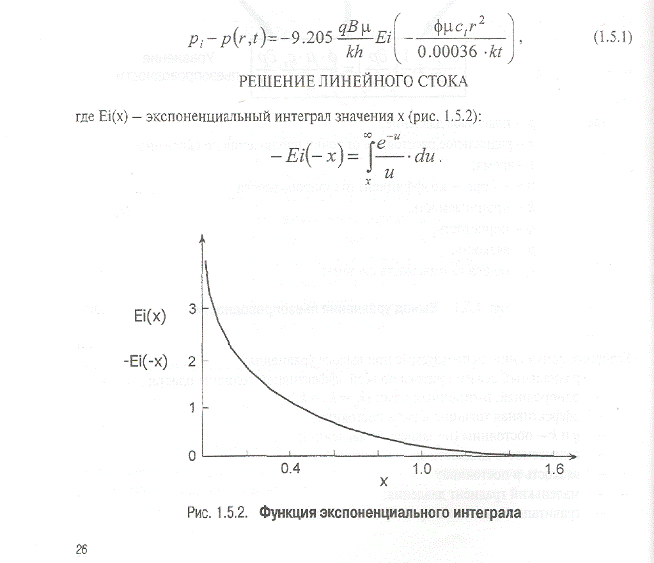
В соответствии с граничными условиями аналитическое решение дифференциального уравнения пьезопроводности примет вид: