ПРИМЕР ПРОЕКТИРОВОЧНОГО РАСЧЕТА ЗУБЧАТОЙ ЦИЛИНДРИЧЕСКОЙ КОСОЗУБОЙ ПЕРЕДАЧИ ВНЕШНЕГО ЗАЦЕПЛЕНИЯ
Рассчитать зубчатую цилиндрическую косозубую передачу одноступенчатого редуктора с моментом на выходе Т2 = 900 Н∙м.
Частоты вращения входного и выходного валов передачи равны п1 =210 об/мин и п2 = 70 об/мин соответственно, т. е. передаточное число и = 3.
Передача нереверсивная, с симметричным расположением шестерни относительно опор. Время безотказной работы t = 10 000 часов в тяжелом режиме нагружения.
В качестве параметров исходного контура инструмента принять:
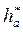 = 1 - коэффициент высоты головки зуба;
= 1 - коэффициент высоты головки зуба;
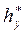 = 1 - коэффициент высоты ножки зуба;
= 1 - коэффициент высоты ножки зуба;
с* = 0,25 - коэффициент радиального зазора;
α = 20° - угол профиля рейки.
1. Выбор материалов и расчет допускаемых напряжений
1.1. Выбор материалов для колеса и шестерни по таблице 5.1
Зубчатые колеса изготовлены из стали 40Х, закаленной по поверхности до твердости НRС 45…50, термообработка типа «улучшение» с последующей закалкой ТВЧ по контуру до заявленной твердости.
1.2. Допускаемые контактные напряжения
шестерня 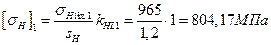 ,
,
колесо 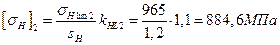 .
.
1.2.1.Пределы контактной выносливости по таблице 5.2
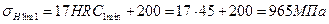 ;
;
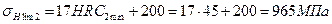 ;
;
1.2.2. Коэффициент запаса прочности 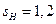 .
.
1.2.3. Коэффициенты долговечности:
- шестерни 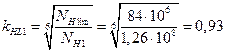 , принимаем
, принимаем 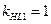 ;
;
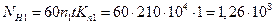 ,
,
- колеса 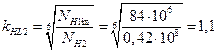 ,
,
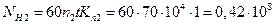
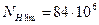 .
.
1.3. Допускаемые напряжения изгиба
шестерни 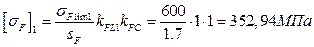
колеса 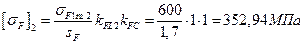
1.3.1. Пределы выносливости зубьев при изгибе:
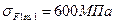 ;
; 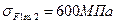 .
.
1.3.2. Коэффициент запаса прочности 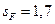 .
.
1.3.3. Коэффициенты долговечности:
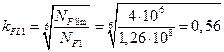
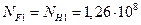
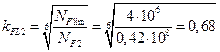 ,
,
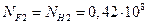 ;
;
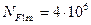 ;
;
Принимаем 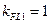 и
и 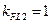 .
.
1.3.4. Коэффициент чувствительности к реверсивной работе
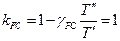 (нереверсивная работа).
(нереверсивная работа).
2. Определение межосевого расстояния аw (мм) из условия прочности по контактным напряжениям
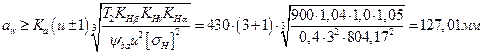 2.1. Коэффициент ширины зубчатого венца относительно межосевого расстояния
2.1. Коэффициент ширины зубчатого венца относительно межосевого расстояния 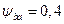 (симметричное расположение относительно опор).
(симметричное расположение относительно опор).
2.2. Коэффициент концентрации нагрузки
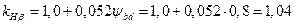 ,
,
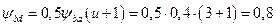 ;
;
2.3. Коэффициент динамичности нагрузки на этапе проектировочного расчета КНv = 1,0.
2.4. Коэффициент неравномерности нагружения зубьев на этапе проектировочного расчета КНα = 1,05.
2.5. Вспомогательный коэффициент Ка = 430 для косозубых и шевронных передач (ГОСТ 21354 – 87).
Полученную величину межосевого расстояния округляем до ближайшего значения из нормального ряда 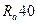 . Принимаем aw = 130 мм.
. Принимаем aw = 130 мм.
3. Определение ширины колеса
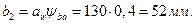
4. Определение ширины шестерни
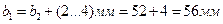
5. Предварительное значение делительного диаметра колеса
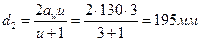
6. Определение ориентировочного значения модуля из расчета прочности по напряжениям изгиба
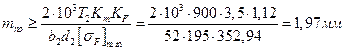 ,
,
6.1. Поправочный коэффициент для косозубых передач 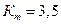 .
.
6.2. Коэффициент расчетной нагрузки KF = KFβKFv = 1,12.
6.2.1. KFβ = 1,124 – коэффициент концентрации нагрузки при расчете напряжений изгиба;
6.2.2. KFv =1,0 – коэффициент динамичности нагрузки (значение, обычно принимаемое на этапе предварительного расчета).
В качестве значения модуля принимаем величину из нормального ряда (ГОСТ 9563 - 80), удовлетворяющуя условию mn ≥ mno, ориентируясь на рекомендацию mn = (0,01…0,02)·aw. В данном случае mn = 2 мм.
7. Определение чисел зубьев колеса и шестерни и угла наклона зубьев
βmin – минимальный угол наклона зубьев (для косозубых и шевронных передач): 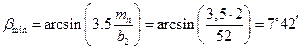
суммарное число зубьев:
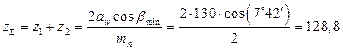 ;
;
Значение zΣ округляем до целого в сторону уменьшения, а именно zΣ = 128;
число зубьев шестерни 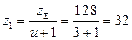 ;
;
число зубьев колеса 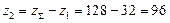
7.1. Уточнение фактического передаточного числа по принятым значениям чисел зубьев:
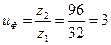 ;
;
Отклонение фактического передаточного числа от заданного не должно превышать 4%: 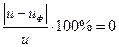 .
.
7.2. Определение действительного угла наклона зубьев
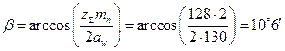 .
.
8. Определение основных геометрических параметров передачи (рис. 9)
8.1. Межосевое расстояние
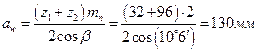
8.2. Диаметры делительных окружностей
шестерни 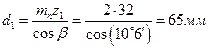
колеса 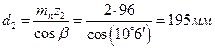 .
.
Передачу проектируем без смещения, полагая х1 = 0 и х2 = 0.
8.3. Диаметры вершин зубьев
шестерни 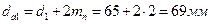 ,
,
колеса 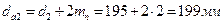
8.4. Диаметры впадин зубьев
шестерни 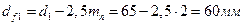 ,
,
колеса 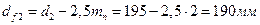
8.5. Коэффициенты перекрытия:
торцового 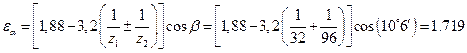 ,
,
осевого 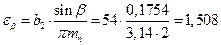 .
.
9. Проверка выполнения условия прочности по контактным напряжениям

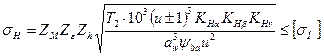 ,
,
9.1. 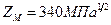 (для стальных колес
(для стальных колес 
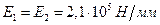 ,
, 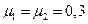 )
)
9.2. 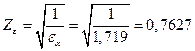 ;
;
9.3. 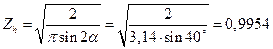 ;
;
9.4. 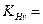 1,01 (выбираем в зависимости от твердости рабочей поверхности, степени точности и окружной скорости);
1,01 (выбираем в зависимости от твердости рабочей поверхности, степени точности и окружной скорости);
9.4.1. Линейная окружная скорость 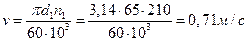
9.4.2. Рекомендуемое значение степени точности (при β> 0)
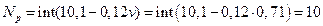
Поскольку на практике детали изготавливаются со степенью точности не ниже 8-й, то назначаем 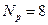 .
.
9.5. 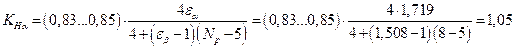
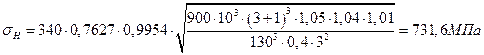
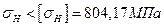 ;
;
Полученное расчетное контактное напряжение должно находиться в интервале 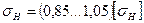 , то есть
, то есть 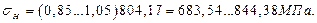
Условие прочности по напряжениям контакта для проектируемой передачи можно считать выполненным.
10. Проверка выполнения условия прочности по напряжениям изгиба
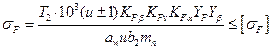 ,
,
10.1. Коэффициент неравномерности нагружения зубьев для косозубых передач
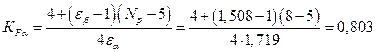 ;
;
10.2. Коэффициент формы зуба определяем при помощи графика, представленного на рисунке 10. Вначале определяем приведенные числа зубьев шестерни и колеса: 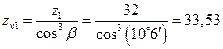 ,
, 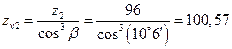 .
.
Соответственно получаем: YF1= 3,75; YF2= 3,6.
10.3. Коэффициент, учитывающий угол наклона зубьев для косозубых и шевронных передач можно приближенно рассчитать по формуле 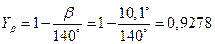 ;
;
10.4. Коэффициент динамичности нагрузки КFv = 1,04 (табл. 1.9.1).
Тогда для шестерни и колеса соответственно имеем:
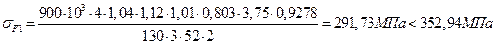
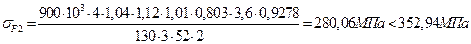
Условие прочности по напряжениям изгиба для проектируемой передачи можно считать выполненным.
11. Силы в зацеплении:
окружная 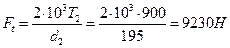 ,
,
радиальная 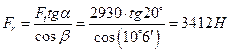 ,
,
осевая 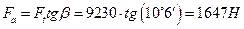
Для решения задачи проектирования зубчатой цилиндрической передачи воспользоваться результатами кинематического расчета, выполненного в задаче 4.
Дата добавления: 2016-01-30; просмотров: 1081;
