МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ
1. Расчет многоступенчатых зубчатых передач следует начи-
нать с тихоходной ступени, как с наиболее нагруженной:
Т3>Т2>Т1.
Выбирать материал зубчатых колес следует с учетом действующих нагрузок. Так как шестерня за одно и то же время совершает большее (в U раз) число оборотов, чем колесо, для ее изготовления должен быть выбран материал, обладающий большим пределом выносливости и большей износостойкостью. Кроме того, твердость поверхности зубьев шестерни после термообработки (нормализации или улучшения) должна превышать твердость поверхности зубьев колеса на 20…40 единиц по Бринеллю. При применении закалки твердость поверхности зубьев колеса и шестерни может быть одинаковой.
Рекомендуемые марки материала и виды термообработки приведены в таблице 5.1
 Таблица 5.1. - Рекомендуемые сочетания материалов, применяемые для изготовления зубчатых колес и шестерен
Таблица 5.1. - Рекомендуемые сочетания материалов, применяемые для изготовления зубчатых колес и шестерен
2. Допускаемые контактные напряжения зубьев при расчете на
усталость определяются по формуле

где σ H lim - предел контактной выносливости материала,
SH - коэффициент безопасности,
KHL – коэффициент долговечности, учитывающий влияние срока службы и режима нагрузки передачи.
Для прямозубых передач, а также для передач с косыми или круговыми зубьями, у которых твердость меньше 350 НВ, за расчетное принимается меньшее из двух допускаемых напряжений, определенных для материала шестерни [σ H ]1 и колеса [σ H]2. Для остальных передач за расчетное принимают среднее из [σ H]1 и
[σ H]2, но не более 1,25[σ H]min для цилиндрических и 1,15[σ H]min для конических, где [σ H]min - меньшее из двух.
Таким образом, для определения [σ H] необходимо предварительно задаться углом наклона зубьев колес β.
β = 0 для прямозубой передачи,
β = 8º… 16º для косозубой передачи,
β = 25º… 40º для сдвоенных косозубых или шевронных колес.
Значение угла β должно соответствовать ряду нормальных значений по ГОСТ 8908-81.
β = …5º, (6º), (7º), 8º, 9º, 10º, (12º), 15º, (18º), 20º, (22º), (25º), 30º, (35º), (40º), 45º …
Значения, указанные в скобках, менее предпочтительны.
Предел контактной выносливости материала σ H lim определяют в зависимости от типа термической или химико-термической обработки в соответствии с рекомендациями в табл. 5.2.
Таблица 5.2. - Определение контактной выносливости материала
| Обработка | Твердость | Материал | σНlim,МПа |
| Улучшение, нормализация | ≤ 350 НВ | Углеродистые и легированные стали | 2 НВ+70 |
| Объемная закалка | 38…50 HRC | 17 HRC+100 | |
| Поверхностна я закалка | 40…56 HRC | 17 HRC+200 | |
| Цементация, нитро-цементация и закалка | 56…65 HRC | Легированные стали | 23 HRC |
| Азотирование | 550…750 HV | ||
| Без обработки | – | Чугун | 2 НВ |
Коэффициент безопасности SH рекомендуется принимать SH ≥ 1,1 при нормализации, улучшении или объемной закалке (т.е. при однородной структуре по объему) и SH ≥ 1,2 при поверхностной закалке, цементации, азотировании (т.е. при неоднородной структуре по объему).
Коэффициент долговечности определяют по формуле
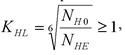
где NH0 – базовое число циклов нагружения, NH0 = 30HB2,4,
HB – твердость материала зубьев по Бриннелю, NHE – эквивалентное число циклов нагружения.
При постоянном режиме нагрузки NHE определяют по формуле
NHE = 60nct0,
где n – частота вращения зубчатого колеса, об/мин,
с – число зацеплений зуба за один оборот колеса (число колес, находящихся в зацеплении с рассчитываемым),
t0 – расчетный срок службы передачи, ч.
3. Методика проектного расчета закрытой зубчатой передачи начинается с определения межосевого расстояния тихоходной ступени по формуле:
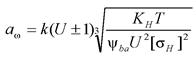
где k- коэффициент, зависящий от угла наклона зубьев: k = 450 для прямозубой передачи, k = 410 для косозубой передачи
U - передаточное число ступени («+» для внешнего зацепления, «-» для внутреннего зацепления);
KH - коэффициент нагрузки, в предварительных расчетах можно принять равным KH = 1,2…1,5, выбирая меньшие значения для более точных передач и при расположении зубчатых колес ближе к середине валов, а большие значения - для менее точных передач при расположении у опор.
T - крутящий момент на ведомом валу ступени, Н∙м;
[σH] – допускаемые контактные напряжения, МПа;
ψba = b/aω – коэффициент ширины зубчатых колес, выбираемый из ряда стандартных значений в соответствии с ГОСТ 2185–66.
При выборе значения ψba необходимо учитывать твердость поверхности зубьев, а также расположение зубчатых колес на валах редуктора так, как это показано в табл. 5.3.
Таблица 5.3 - Определение коэффициента ширины
| Твердость | Расположение | ||
| Симметричное | Несимметричное | Консольное | |
| HB ≤ 350 | ψba = 0,315; 0,4; 0,5 | ψba = 0,25; 0,315; 0,4 | ψba = 0,2; 0,25 |
| HB > 350 | ψba = 0,25; 0,315; 0,4 | ψba = 0,2; 0,25; 0,315 | ψba = 0,16; 0,2 |
Полученное значение межосевого расстояния необходимо округлить до ближайшего стандартного значения по ГОСТ 2185-66.
aω = 40, 50, 63, (71), 80, (90), 100, (112), 125, (140), 160, (180), 200, (224), 250, (280), 315, (355), 400, (450), 500 и т.д.
В скобках указаны менее предпочтительные значения.
По окружной скорости зубчатого венца тихоходного колеса определить правильность выбора угла наклона зубьев:

Если ν > 3,5 м/c для прямозубой передачи, то следует применить косозубое зацепление и заново проделать расчет.
4. Предварительно выбрать стандартное значение нормального модуля зацепления mn по ГОСТ 9563-60 из рекомендуемого интервала значений:
mn = (0,01… 0,02)a ω для улучшенных зубчатых колес;
mn = (0,015…0,0315)a ω для закаленных зубчатых колес;
mn = … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10 …
При этом необходимо учесть, что меньший модуль обеспечивает больший коэффициент перекрытия, повышая тем самым плавность работы передачи, но одновременно понижает несущую способность передачи по напряжениям изгиба.
5. Далее следует определить суммарное число зубьев для пары зубчатых колес и округлить его до ближайшего целого, если оно получится дробным
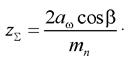
 Числа зубьев для каждого из зубчатых колес определятся по формулам
Числа зубьев для каждого из зубчатых колес определятся по формулам
Если z1 < 17, то, во избежание корригирования зацепления, можно уменьшить значение модуля зацепления mn.
Далее необходимо проверить соответствие полученного межосевого расстояния предварительно принятому
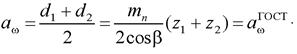
Если равенство не выполняется, то следует изменить значение нормального модуля зацепления mn. Для косозубого зацепления можно изменить угол наклона зубьев β и принять его равным

При этом угол β должен соответствовать нормальному ряду значений по ГОСТ 8908-58.
Далее необходимо провести проверку кинематической точности передачи и определить отклонение полученного передаточного числа от исходного:
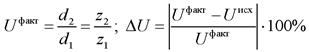
Если отклонение ΔU превышает 2% для U < 4 или 4% для U ≥ 4, то следует пересмотреть значение нормального модуля зацепления mn.
6. В конце проектного расчета зубчатой передачи следует определить диаметры вершин da и диаметры впадин df зубьев, а также ширину b зубчатых венцов, находящихся в зацеплении:
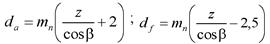
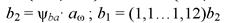
Численные значения ширины зубчатых венцов округляются до
ближайшего числа из ряда Ra20 по ГОСТ 6636-69.
Также следует задать степень точности изготовления зубчатой
передачи по ГОСТ 1643-81 (для цилиндрических передач) или по
ГОСТ 9368-81 (для конических передач), руководствуясь табл. 5.4.
Таблица 5.4 - Степени точности зубчатых передач
| Вид зубьев | Вид передачи | Твердость | Степень точности | |||
| Окружная скорость, м/с | ||||||
| Прямые | Цилиндрическая | НВ ≤ 350 | ≤ 18 | ≤ 12 | ≤ 6 | ≤ 4 |
| НВ > 350 | ≤ 15 | ≤ 10 | ≤ 5 | ≤ 3 | ||
| Коническая | НВ ≤ 350 | ≤ 10 | ≤ 7 | ≤ 4 | ≤ 3 | |
| НВ > 350 | ≤ 9 | ≤ 6 | ≤ 3 | ≤ 2,5 | ||
| Непрямые | Цилиндри ческая | НВ ≤ 350 | ≤ 36 | ≤ 25 | ≤ 12 | ≤ 8 |
| НВ > 350 | ≤ 30 | ≤ 20 | ≤ 9 | ≤ 6 | ||
| Коническаяая | НВ ≤ 350 | ≤ 24 | ≤ 16 | ≤ 9 | ≤ 6 | |
| НВ > 350 | ≤ 19 | ≤ 13 | ≤ 7 | ≤ 5 |
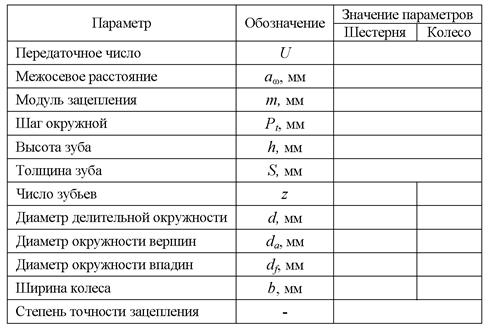
Основные параметры зубчатого зацепления свести в таблицу
5.5.
Таблица 5.5 - Основные параметры зацепления
7. Проверочный расчет зубчатой передачи по контактным напряжениям
 Проверочный расчет зубчатой передачи по контактным напряжениям заключается в определении отклонения Δσ действительных контактных напряжений оН от максимально допустимых [он] и сравнении этого отклонения с рекомендуемым интервалом значений.
Проверочный расчет зубчатой передачи по контактным напряжениям заключается в определении отклонения Δσ действительных контактных напряжений оН от максимально допустимых [он] и сравнении этого отклонения с рекомендуемым интервалом значений.
Для некорригированных стальных зубчатых колес действительные контактные напряжения определяются по формуле:
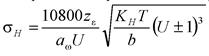 ,
,
где U = z2/z1– передаточное число ступени;
a ω - межосевое расстояние, мм;
Т - крутящий момент, Н∙м;
b - ширина зубчатого венца, мм;
zε - коэффициент, учитывающий плавность зацепления, и зависящий от коэффициента перекрытия зубьев εα:
 - для прямозубых колес
- для прямозубых колес
 - для косозубых колес
- для косозубых колес


KH = KHαKHβKHυ - коэффициент нагрузки, учитывающий неравномерность распределения нагрузки между зубьями и по ширине венца, а также возможные динамические нагрузки в зацеплении.
KH α - коэффициент распределения нагрузки:
KH α = 1 для прямозубых передач,
KHα = 1,05…1,15 для косозубых и шевронных передач, где большие значения принимают при больших окружных скоростях и больших степенях точности.
KHβ - коэффициент концентрации нагрузки, определяемый по табл. 5.6 в зависимости от твердости поверхности зубьев колеса, относительных размеров шестерни и схемы передачи.
Коэффициент динамичности KHυ определяем по таблице 5.7 в зависимости от окружной скорости, степени точности и твердости рабочих поверхностей зубьев.
Таблица 5.6 - Значения коэффициента концентрации KHβ
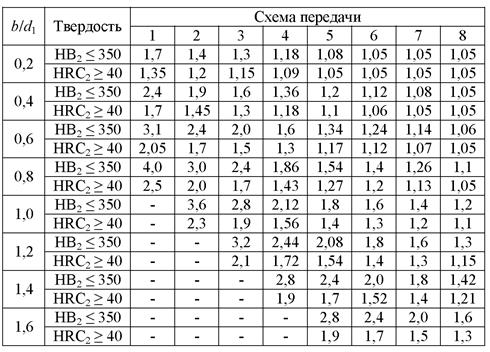
 Таблица 5.6 - Значения коэффициента концентрации KHv
Таблица 5.6 - Значения коэффициента концентрации KHv
8. Проверочный расчет зубчатой передачи по напряжениям изгиба
Зубчатое зацепление считается проходящим проверку на выносливость по напряжениям изгиба, если соблюдается условие
oF ≤ 1,05[σF], т.е. фактические напряжения изгиба практически не превышают допускаемых. Для проверки этого условия необходимо вначале определить допускаемые напряжения изгиба.

где σ F lim - предел изгибной выносливости материала,
SF - коэффициент безопасности,
КFL- коэффициент долговечности, учитывающий влияние срока службы и режима нагрузки передачи.
Предел изгибной выносливости материала σmin и коэффициент безопасности SF определяют в зависимости от типа термической или химико-термической обработки в соответствии с рекомендациями, представленными в табл. 5.7.
Коэффициент долговечности определяют по формуле
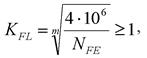
где m = 9 при твердости поверхности зубьев HB > 350, m = 6 при твердости поверхности зубьев HB < 350
NFE - эквивалентное число циклов нагружения.
Таблица 5.7. – определение изгибной выносливости материала
| Вид обработки | Твердость | Материал | σМim,МПа | SF |
| Нормализация, улучшение | 180…350 HB | 40, 45, 40Х, 40ХН, 45ХЦ, 35ХМ … | 1,75 HB | 1,7 |
| Объемная закалка | 45…55 HRC | 40Х, 40ХН, 35ХМ … | 500…550 | |
| Закалка ТВЧ с охватом впадин | 48…52 HRC | 40Х, 35ХМ, 40ХН | 500…600 | |
| Закалка ТВЧ по всему контуру | 56…62 HRC | 58, 45РП, У6 | ||
| 48…52 HRC | 40Х, 40ХН, 35ХМ | 600…700 | ||
| Азотирование | 700…950 HV | 38Х2Ю, 38Х2МЮА | 12 HRC + 290 | |
| 550…750 HV | 40Х, 40ХФА, 40Х2НМА | |||
| Цементация | 57…62 HRC | Легированные стали | 750…800 | 1,55 |
| Нитроцементация | 56…63 HRC | 25ХГМ | ||
| 25ХГТ, 30ХГТ, 35Х |
При постоянном режиме нагрузки NFE определяют по формуле
NFE = 60nct0,
где n – частота вращения зубчатого колеса, об/мин;
с – число зацеплений зуба за один оборот колеса (число колес, находящихся в зацеплении с рассчитываемым);
t0 – расчетный срок службы передачи, ч.
Фактические напряжения изгиба определяют отдельно для колеса и для шестерни по следующей формуле:

где Ft – окружная сила в зацеплении, определяемая по формуле:

гдеT1, T2 – крутящие моменты на ведущем и ведомом валах соответственно, d2, d1 – делительные диаметры зубчатого колеса и шестерни соответственно.
b – ширина зубчатого венца;
mn – нормальный модуль зацепления;
YF – коэффициент формы зуба, принимаемый по табл. 5.8 в зависимости от эквивалентного числа зубьев zν и коэффициента коррекции зацепления χ.
Таблица 5.8 - Значения коэффициента формы зуба YF
| zν | χ | ||||||||
| -0,5 | -0,4 | -0,25 | -0,16 | +0,16 | +0,25 | +0,4 | +0,5 | ||
| - | - | - | - | - | - | - | 3,68 | 3,46 | |
| - | - | - | - | 4,28 | 4,02 | 3,78 | 3,54 | 3,40 | |
| - | - | - | 4,40 | 4,07 | 3,83 | 3,64 | 3,50 | 3,39 | |
| - | - | 4,30 | 4,13 | 3,90 | 3,72 | 3,62 | 3,47 | 3,40 | |
| 4,50 | 4,27 | 4,05 | 3,94 | 3,78 | 3,65 | 3,59 | 3,46 | 3,40 | |
| 4,14 | 4,02 | 3,88 | 3,81 | 3,70 | 3,61 | 3,57 | 3,48 | 3,42 | |
| 3,96 | 3,88 | 3,78 | 3,73 | 3,68 | 3,58 | 3,54 | 3,49 | 3,44 | |
| 3,82 | 3,78 | 3,71 | 3,68 | 3,62 | 3,57 | 3,54 | 3,50 | 3,47 | |
| 3,79 | 3,74 | 3,68 | 3,66 | 3,61 | 3,56 | 3,55 | 3,50 | 3,48 | |
| 3,73 | 3,70 | 3,66 | 3,63 | 3,60 | 3,55 | 3,55 | 3,51 | 3,50 | |
| 3,70 | 3,68 | 3,64 | 3,62 | 3,60 | 3,55 | 3,55 | 3,53 | 3,51 | |
| 3,68 | 3,66 | 3,62 | 3,61 | 3,60 | 3,56 | 3,56 | 3,55 | 3,52 | |
| 3,64 | 3,62 | 3,62 | 3,62 | 3,62 | 3,59 | 3,58 | 3,56 | 3,56 | |
| > 180 | 3,63 |
Y β - коэффициент наклона зуба, определяемый по формуле

где β - угол подъема линии зуба, градусы.
KF = KFαKF βKFυ - коэффициент нагрузки, учитывающий неравномерность распределения нагрузки между зубьями и по ширине венца, а также возможные динамические нагрузки в зацеплении.
KFα - коэффициент распределения нагрузки:
KFα = 1 для прямозубых передач; для косозубых и шевронных передач KFα зависит от степени точности зацепления:
| Степень точности | ||||
| Kfα | 0,72 | 0,81 | 0,91 | 1,00 |
KF β - коэффициент концентрации нагрузки, определяемый по таблице 5.9 в зависимости от твердости поверхности зубьев колеса, относительных размеров шестерни и схемы передачи.
KFυ - коэффициент динамичности, определяемый по таблице 5.10 в зависимости от окружной скорости, степени точности и твердости рабочих поверхностей зубьев.
В случае невыполнения условия oF ≤ [oF] следует изменить либо значения модуля зацепления mn, либо ширину зубчатых колес b1 и b2, либо выбрать более прочные материалы для их изготовления.
Таблица 5.9 - Значения коэффициента концентрации КFb
| b/d1 | Твердость | Схема передачи | |||||||
| 0,2 | HB2 ≤ 350 | 1,53 | 1,31 | 1,23 | 1,15 | 1,07 | 1,04 | 1,04 | 1,04 |
| HRC2 ≥ 40 | 1,25 | 1,16 | 1,12 | 1,08 | 1,04 | 1,04 | 1,04 | 1,04 | |
| 0,4 | HB2 ≤ 350 | 2,01 | 1,67 | 1,46 | 1,27 | 1,16 | 1,09 | 1,06 | 1,04 |
| HRC2 ≥ 40 | 1,53 | 1,34 | 1,23 | 1,13 | 1,08 | 1,05 | 1,04 | 1,04 | |
| 0.6 | HB2 ≤ 350 | 2,47 | 2,01 | 1,74 | 1,46 | 1,26 | 1,16 | 1,08 | 1,06 |
| HRC2 ≥ 40 | 1,75 | 1,53 | 1,38 | 1,23 | 1,14 | 1,08 | 1,06 | 1,04 | |
| 0.8 | HB2 ≤ 350 | 3,03 | 2,41 | 2,01 | 1,62 | 1,41 | 1,31 | 1,21 | 1,08 |
| HRC2 ≥ 40 | 2,08 | 1,74 | 1,53 | 1,32 | 1,21 | 1,16 | 1,08 | 1,04 | |
| 1.0 | HB2 ≤ 350 | - | 2,8 | 2,28 | 1,82 | 1,6 | 1,46 | 1,31 | 1,16 |
| HRC2 ≥ 40 | - | 1,95 | 1,67 | 1,42 | 1,31 | 1,23 | 1,16 | 1,08 | |
| 1.2 | HB2 ≤ 350 | - | - | 2,54 | 2,04 | 1,8 | 1,6 | 1,46 | 1,23 |
| HRC2 ≥ 40 | - | - | 1,81 | 1,53 | 1,42 | 1,31 | 1,23 | 1,11 | |
| 1.4 | HB2 ≤ 350 | - | - | - | 2,28 | 2,01 | 1,74 | 1,6 | 1,32 |
| HRC2 ≥ 40 | - | - | - | 1,67 | 1,53 | 1,4 | 1,31 | 1,16 | |
| 1.6 | HB2 ≤ 350 | - | - | - | - | 2,23 | 2,01 | 1,74 | 1,46 |
| HRC2 ≥ 40 | - | - | - | - | 1,67 | 1,53 | 1,38 | 1,23 |
Таблица 5.10 - Значения коэффициента динамичности KFυ
| Степень точности | Твердость | β | υ, м/с | |||||
| точности | ть | |||||||
| HB2 ≤ 350 | β = 0 | 1,06 | 1,13 | 1,26 | 1,40 | 1,58 | 1,67 | |
| β ≠ 0 | 1,02 | 1,05 | 1,10 | 1,15 | 1,20 | 1,25 | ||
| HRC2 ≥ 40 | β = 0 | 1,02 | 1,04 | 1,08 | 1,11 | 1,14 | 1,17 | |
| β ≠ 0 | 1,01 | 1,02 | 1,03 | 1,04 | 1,06 | 1,07 | ||
| HB2 ≤ 350 | β = 0 | 1,08 | 1,16 | 1,33 | 1,50 | 1,67 | 1,80 | |
| β ≠ 0 | 1,03 | 1,06 | 1,11 | 1,16 | 1,22 | 1,27 | ||
| HRC2 ≥ 40 | β = 0 | 1,03 | 1,05 | 1,09 | 1,13 | 1,17 | 1,22 | |
| β ≠ 0 | 1,01 | 1,02 | 1,03 | 1,05 | 1,07 | 1,08 | ||
| HB2 ≤ 350 | β = 0 | 1,10 | 1,20 | 1,38 | 1,58 | 1,78 | 1,96 | |
| β ≠ 0 | 1,03 | 1,06 | 1,11 | 1,17 | 1,23 | 1,29 | ||
| HRC2 ≥ 40 | β = 0 | 1,04 | 1,06 | 1,12 | 1,16 | 1,21 | 1,26 | |
| β ≠ 0 | 1,01 | 1,02 | 1,03 | 1,05 | 1,07 | 1,08 | ||
| HB2 ≤ 350 | β = 0 | 1,13 | 1,28 | 1,50 | 1,77 | 1,98 | 2,25 | |
| β ≠ 0 | 1,04 | 1,07 | 1,14 | 1,21 | 1,28 | 1,35 | ||
| HRC2 ≥ 40 | β = 0 | 1,04 | 1,07 | 1,14 | 1,21 | 1,27 | 1,34 | |
| β ≠ 0 | 1,01 | 1,02 | 1,04 | 1,06 | 1,08 | 1,09 |
9. Силы в зацеплении:
окружная, 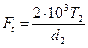
радиальная , 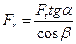
осевая 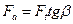 .
.
Дата добавления: 2016-01-30; просмотров: 1118;
