Энергия работа кинетическая, потенциальное энергия закон сохранения энергий
Когда под действием некоторой силы тело совершает перемещение, то действие силы характеризуется величиной, которая называется механической работой.
Механическая работа- мера действия силы, в результате которого тела совершают перемещение.
Р 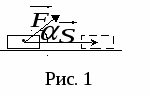
 абота постоянной силы.Если тело движется прямолинейно под действием постоянной силы
абота постоянной силы.Если тело движется прямолинейно под действием постоянной силы 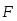 , составляющей некоторый уголaс направлением перемещения
, составляющей некоторый уголaс направлением перемещения  (рис.1), работа равна произведению этой силы на перемещение точки приложения силы и на косинус углаaмежду векторами и
(рис.1), работа равна произведению этой силы на перемещение точки приложения силы и на косинус углаaмежду векторами и 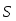 ; или работа равна скалярному произведению вектора силы на вектор перемещения:
; или работа равна скалярному произведению вектора силы на вектор перемещения:
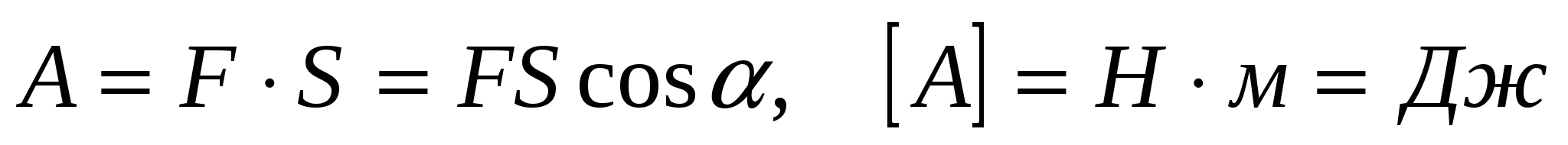 .
.
1 Дж - работа, совершаемая силой в 1Н при перемещении на 1м в направлении действия силы.
1. если a- острый угол, 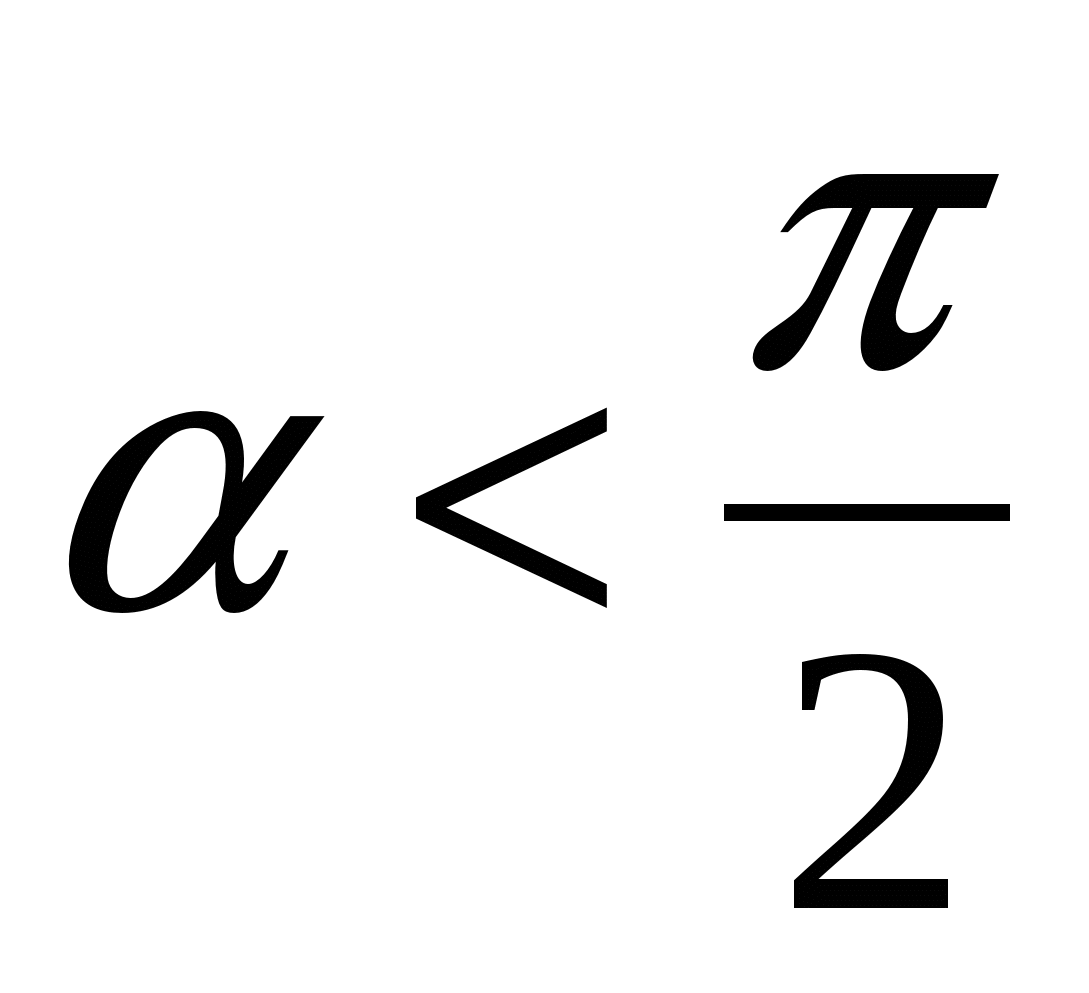 ,
, 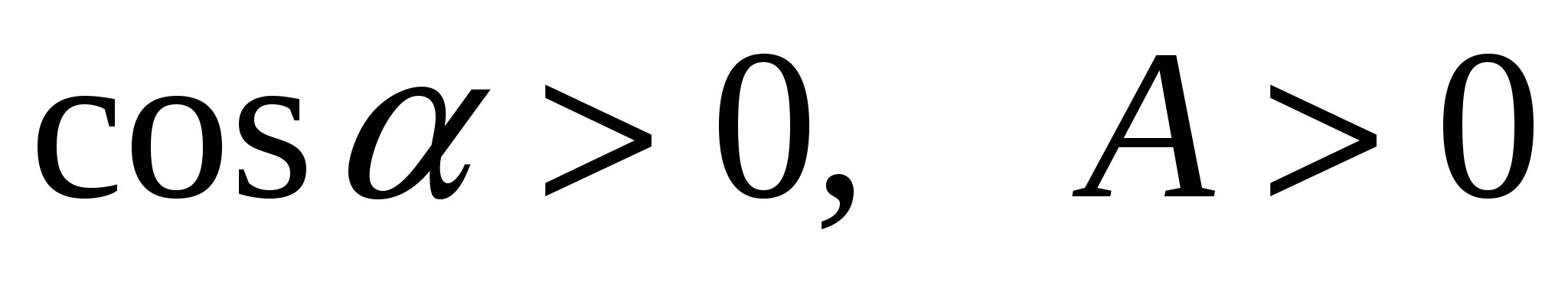 ;
;
2. если a- тупой угол, 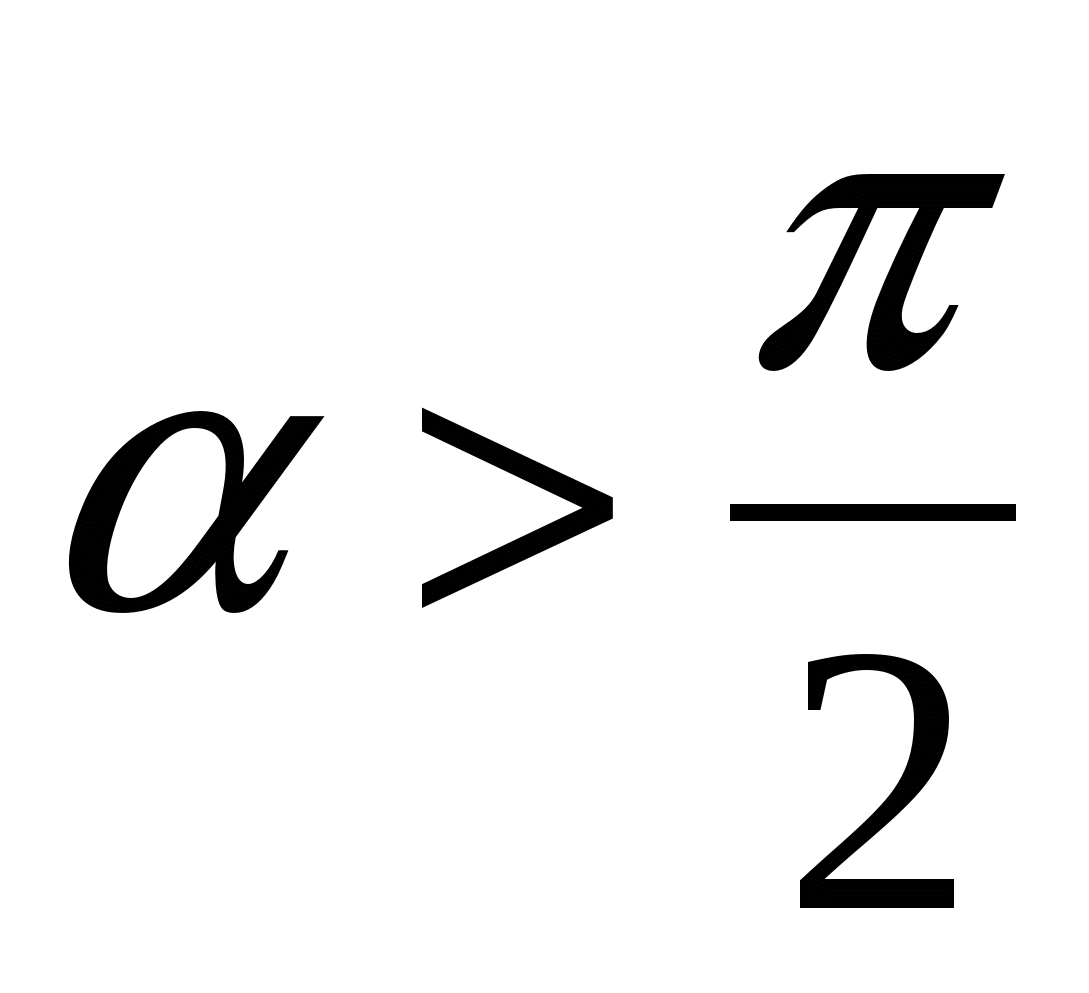 ,
,  ;
;
3. если 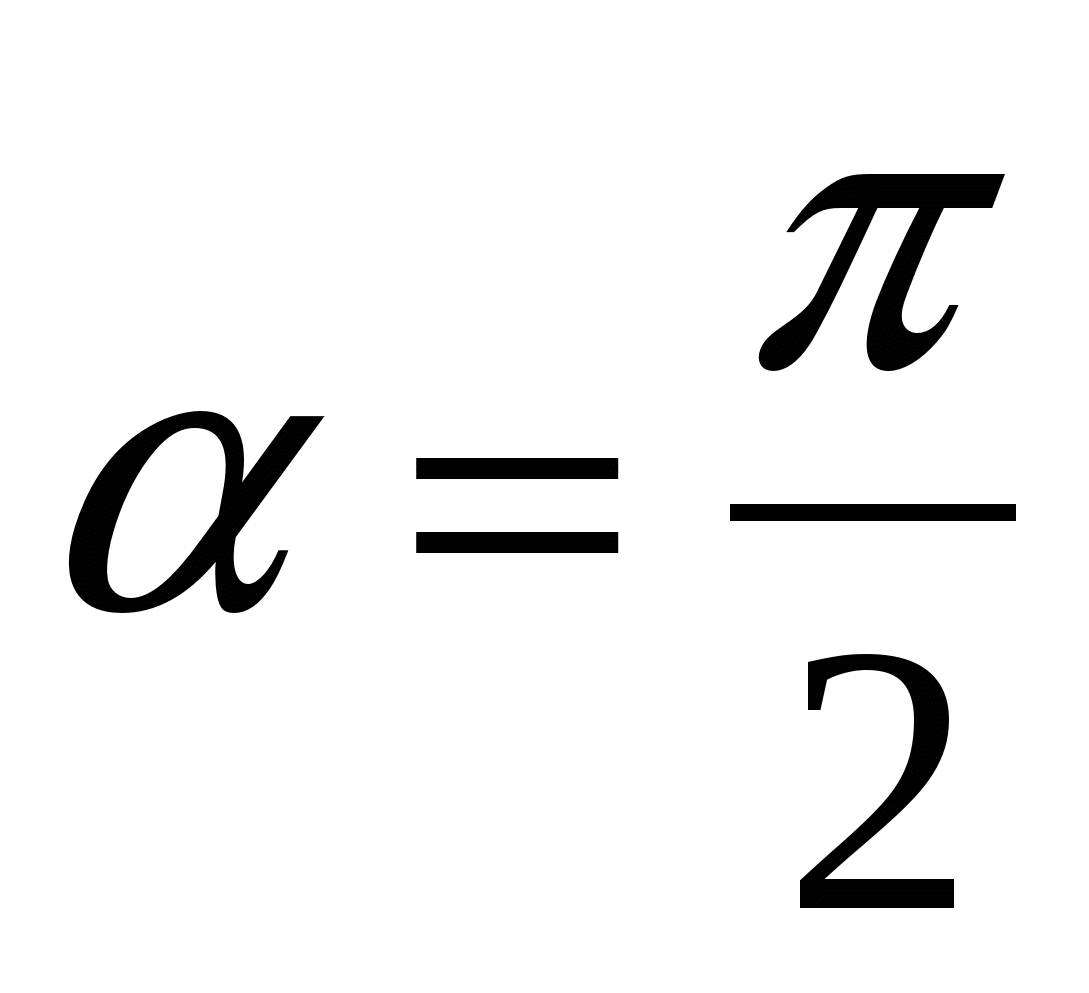 ,
, 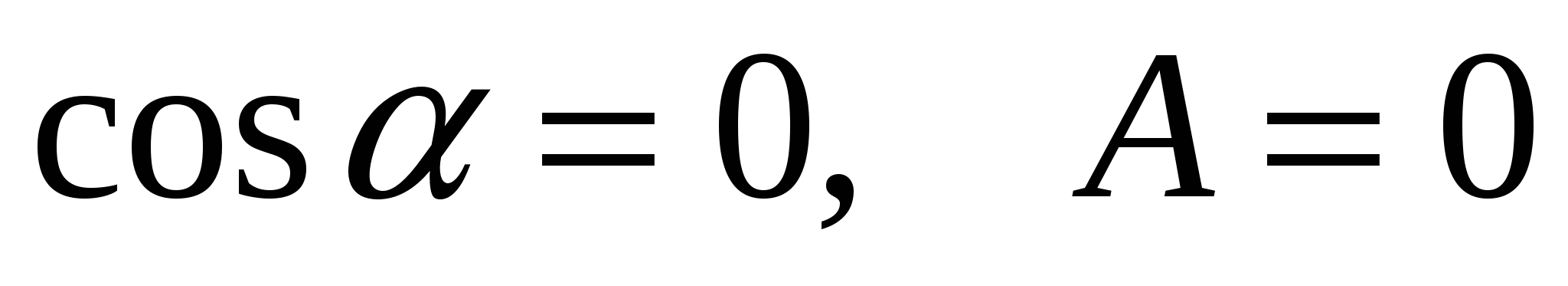 .
.
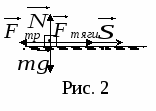
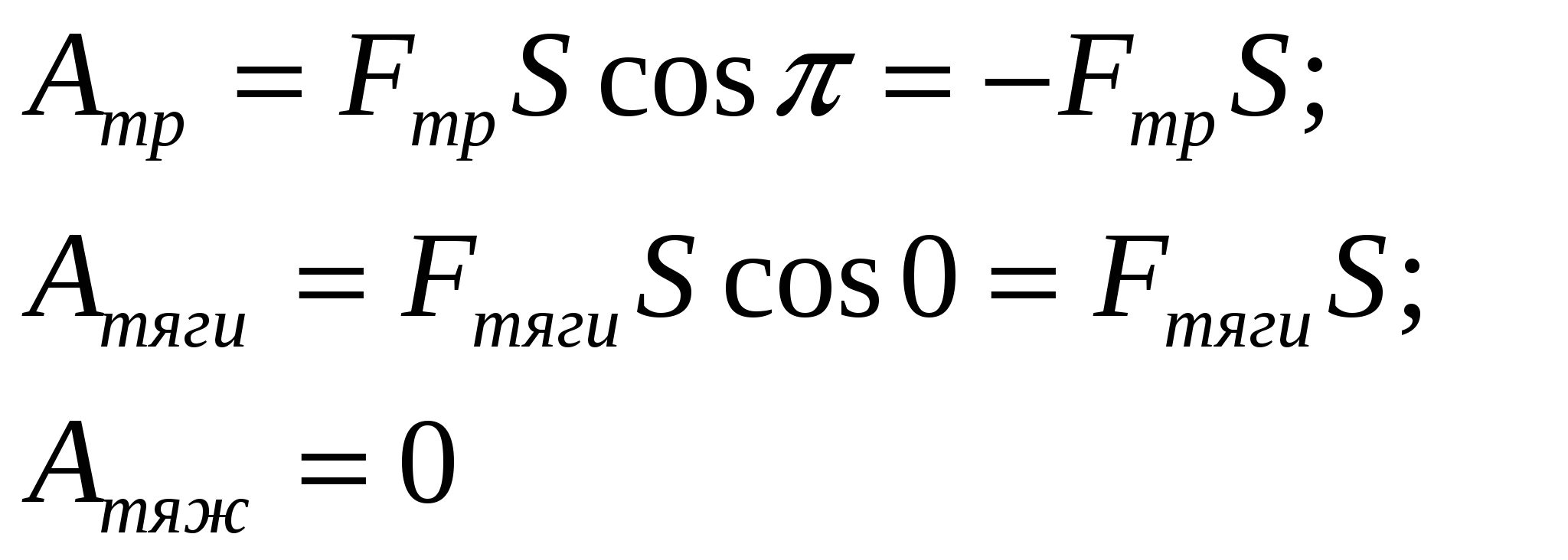
Работа переменной силы. Чтобы найти работу переменной силы, пройденный путь разбивают на большое число малых участков так, чтобы их можно было считать прямолинейными, а действующую в любой точке данного участка силу - постоянной.
Элементарная работа (т.е. работа на элементарном участке 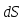 ) равна
) равна 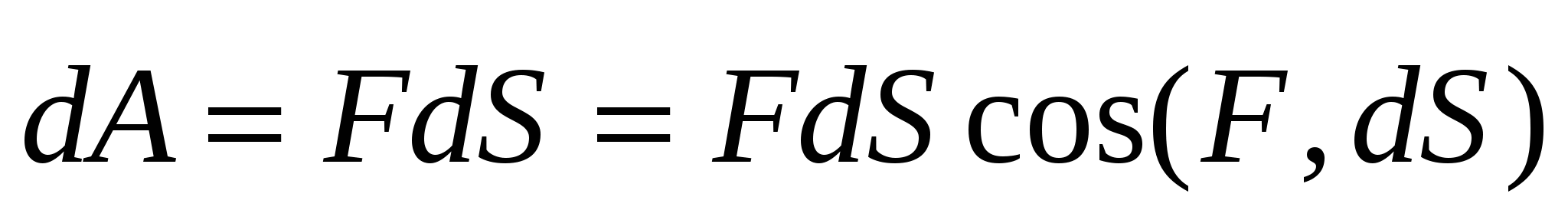 , а вся работа переменной силы на всем путиSнаходится интегрированием:
, а вся работа переменной силы на всем путиSнаходится интегрированием: 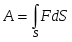 .
.
В качестве примера работы переменной силы рассмотрим работу, совершаемую при деформации (растяжении) пружины, подчиняющейся закону Гука.
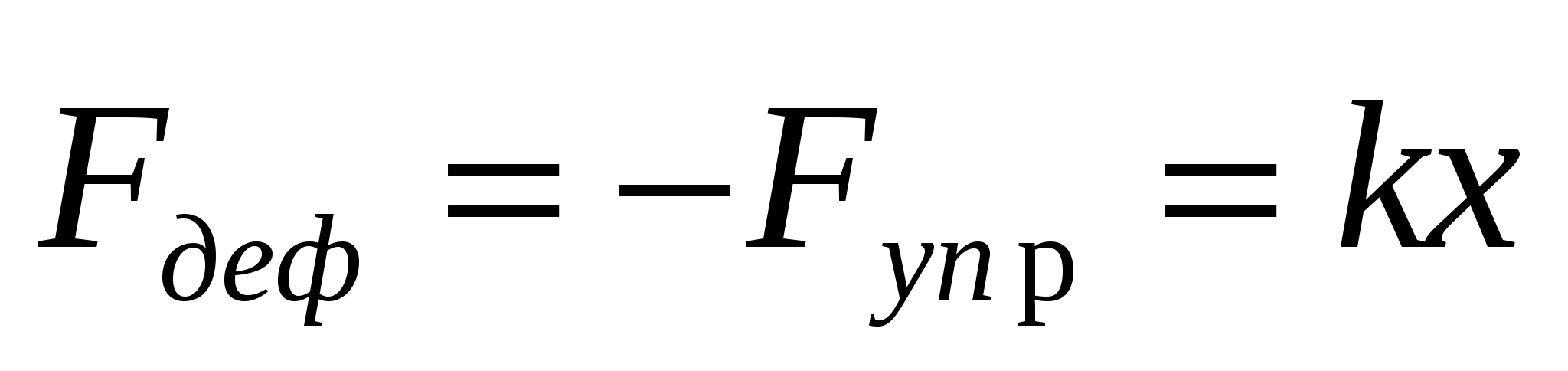
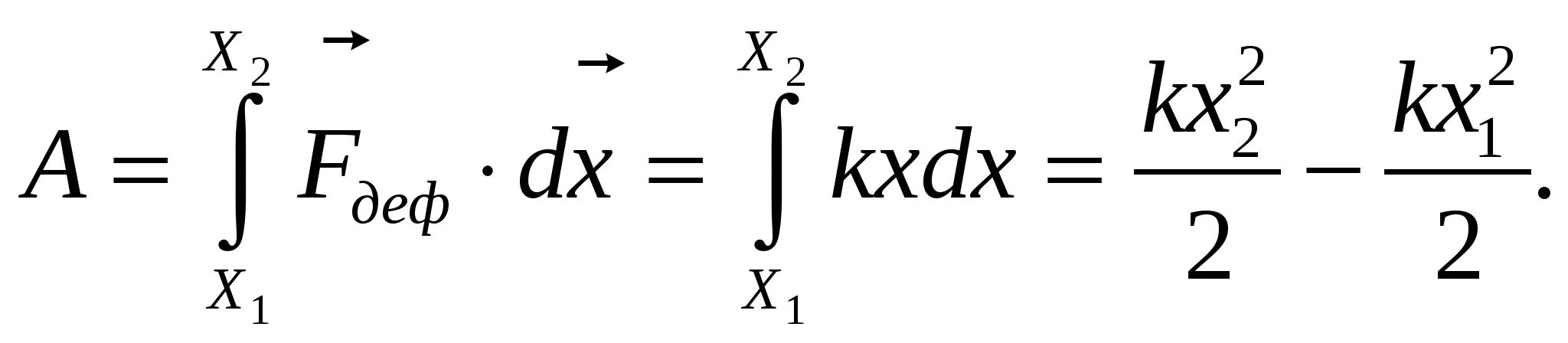
Если начальная деформация x1=0, то 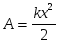 .
.
При сжатии пружины совершается такая же работа.
Г 
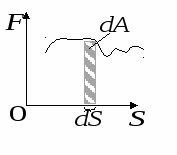 рафическое изображение работы (рис.3).
рафическое изображение работы (рис.3).
На графиках работа численно равна площади заштрихованных фигур.
Для характеристики быстроты совершения работы вводят понятие мощности.
Мощность постоянной силы численно равна работе, совершаемой этой силой за единицу времени.
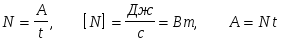 .
.
1 Вт- это мощность силы, которая за 1 с совершает 1 Дж работы.
В случае переменной мощности (за малые одинаковые промежутки времени совершается различная работа) вводится понятие мгновенной мощности:
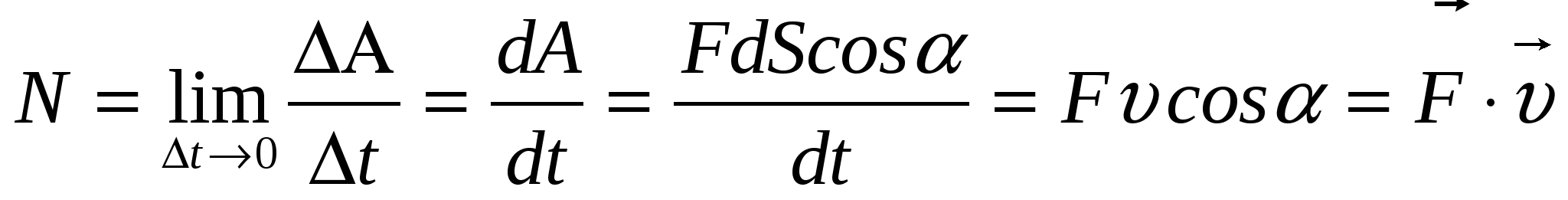 ,
,
где 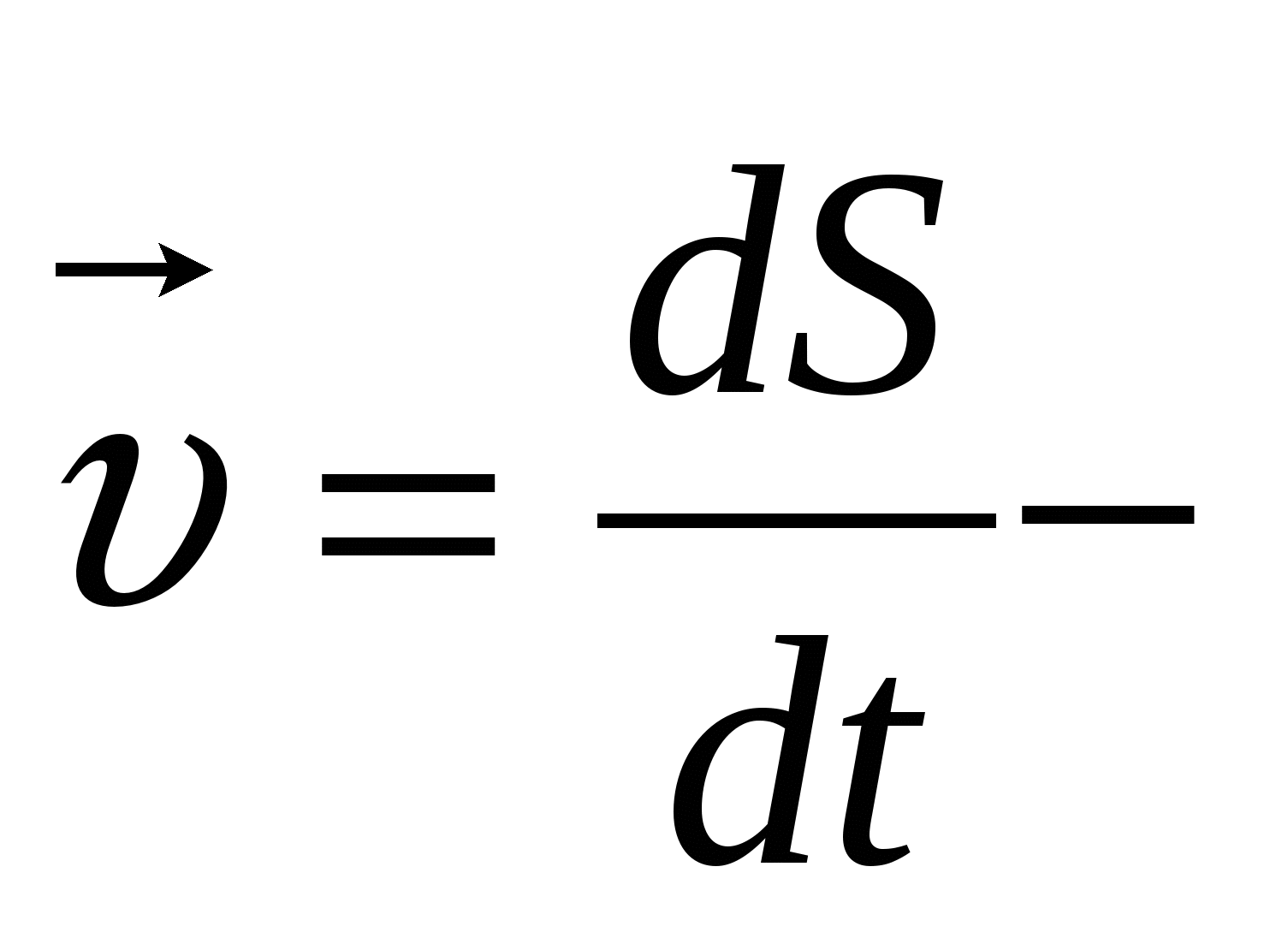 скорость точки приложения силы.
скорость точки приложения силы.
Т.о. мощность равна скалярному произведению силы на скорость 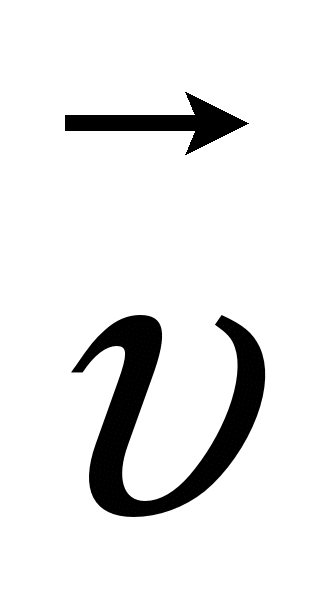 точки её приложения.
точки её приложения.
Т.к. 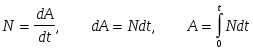
Дата добавления: 2016-01-30; просмотров: 871;
