Теорема Штейнера — формулировка
Согласно теореме Штейнера, установлено, что момент инерции тела при расчете относительно произвольно оси соответствует сумме момента инерции тела относительно такой оси, которая проходит через центр масс и является параллельной данной оси, а также плюс произведение квадрата расстояния между осями и массы тела, по следующей формуле (1):
J= J0 + md2 (1)
Где в формуле принимаем соответственно величины: d – расстояние между осями ОО1║О’O1’;
J0 – момент инерции тела, рассчитанный относительно оси, что проходит сквозь центр масс и будет определяться соотношением (2):
J0 = Jd = mR2/2 (2)
| Вопрос | Какой формулировке отвечает теорема Штейнера? | |
| Ответ | момент инерции тела I относительно произвольной оси равен сумме момента инерции этого тела IС относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями
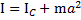 .
Например, для обруча на рисунке момент инерции относительно оси O’O’, равен .
Например, для обруча на рисунке момент инерции относительно оси O’O’, равен
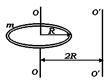 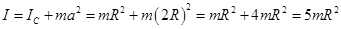 Момент инерции прямого стержня длиной
Момент инерции прямого стержня длиной 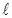 , ось перпендикулярна стержню и проходит через его конец. , ось перпендикулярна стержню и проходит через его конец.
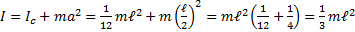
|
Дата добавления: 2016-01-30; просмотров: 8827;
