Ускорение под действием силы тяжести

Галилей показал, что падающее дело движется равноускоренно, то есть его скорость увеличивается на одну и ту же величину за одинаковые промежутки времени. Сейчас мы эту закономерность выражаем так: тело, изначально находившееся в покое, спустя время t от момента начала падения приобретет скорость v , пропорциональную t :

v = gt ,

где g – константа, которая характеризует поле силы тяжести на поверхности Земли. Хотя g несколько отличается в различных точках земной поверхности, она нигде не отклоняется значительно от 9,8 м/с за секунду.

Согласно теореме о средней скорости расстояние, которое преодолеет такое падающее тело с момента начала падения до t , будет равняться v_средt , где v_сред – среднее арифметическое между величиной gt и нулем, то есть vсред = gt /2. Следовательно, расстояние, проходимое за время падения, равно:

В частности, за первую секунду падения тело пролетает g (1 секунда)²/2 = 4,9 м. Время, которое требуется падающему телу, чтобы пройти заданное расстояние, в общем случае равно:

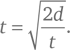
На полученный результат можно взглянуть с иной, более современной точки зрения. Полная энергия падающего тела равна сумме двух слагаемых: его кинетической и потенциальной энергии. Кинетическая энергия выражается как:

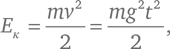
где m – масса тела. Потенциальная энергия – это произведение mg на текущую высоту (измеряемую относительно любого произвольно выбранного уровня). Поэтому если тело сбрасывается с некоторой начальной высоты h ₀ и проходит в падении расстояние d , то его потенциальная энергия равна:

Значит, учитывая, что d = gt² /2, полная энергия тела – постоянная величина:

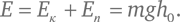
Это правило мы можем обратить и вывести соотношение между скоростью и пройденным расстоянием, беря за основу закон сохранения энергии. Если в нулевой момент времени t = 0, когда v = 0 и h = h ₀, мы считаем полную энергию E равной mgh ₀, то согласно закону сохранения энергии в любой момент времени справедливо:

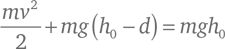
из чего следует, что v ²/2 = gd . Поскольку v – это мера того, как увеличивается d , то, что мы получаем, – это дифференциальное уравнение, определяющее связь между d и t . Конечно, мы уже знаем решение этого уравнения: d = gt ²/2, при этом v = gt . Таким образом, используя закон сохранения энергии, мы можем получить те же самые результаты, не зная заранее, что ускорение падающего тела постоянно.

Мы увидели элементарный пример использования этого закона, который позволяет разнообразно применять понятие об энергии. В частности, закон сохранения энергии доказывает правильность того, что эксперименты Галилея с шариками, скатывающимися по наклонной плоскости, верно моделируют задачу о свободном падении, хотя сам Галилей не приводил его в качестве аргумента. Для шарика массой m , скатывающегося по наклонной плоскости, кинетическая энергия равна mv ²/2, причем здесь v – скорость движения шарика вдоль плоскости, а потенциальная энергия равняется mgh , где h – текущая высота шарика. Дополнительным слагаемым тут служит энергия вращения шарика, которая выражается таким образом:

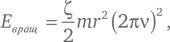
где r – радиус шарика, ν – число полных оборотов катящегося шарика в секунду, а ζ – величина, которая зависит от распределения массы внутри самого шарика и его формы. Применительно к экспериментам Галилея, который, скорее всего, использовал сплошные твердые шары, значение ζ = 2/5 (для пустотелого шара, например, ζ = 2/3). Теперь заметим, что, когда шарик совершает один полный оборот, он проходит расстояние, равное длине его окружности 2πr , поэтому в течение времени t , за которое он совершает νt оборотов, полное пройденное расстояние составляет d = 2πr νt , и значит, его скорость равняется d /t = 2π νr . Подставляя это выражение в формулу энергии вращательного движения, получаем:

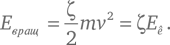
Поделив обе части на m и на 1 + ζ, используем закон сохранения энергии и получим уравнение:

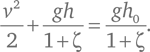
Это та же самая зависимость между скоростью и перепадом высоты d = h ₀ – h , которая справедлива и для свободно падающего тела, с тем лишь отличием, что g заменяется на g /(1 + ζ). Если эту замену не учитывать, зависимость скорости шарика, катящегося вниз по наклонной плоскости, от проходимого перепада высоты та же самая, что и для тела в свободном падении. Это означает, что, изучая скатывание шаров по наклонной плоскости, можно доказать, что и свободно падающие тела движутся равноускоренно. Однако таким образом нельзя рассчитать ускорение, если не учитывать реальное значение коэффициента 1/(1 + ζ).

Путем сложных доказательств Гюйгенс сумел выразить время, которое требуется маятнику длины L , чтобы переместиться с одной стороны на другую с небольшим углом, равенством:

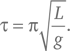
Полученный Гюйгенсом результат означал, что это время в π раз больше, чем то время, которое нужно падающему телу, чтобы пройти расстояние d = L /2.