Главные оси инерции

Если тело имеет ось симметрии OZ, то:

;

,

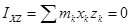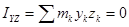так как точки k и k' попарно симметричны относительно оси OZ, то .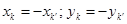

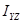Ось Z, для которой центробежные моменты инерции и , содержащие в своих индексах наименование этой оси, равны нулю, называется главной осью инерции тела для точки О, через которую проходит ось Z.

Если тело имеет ось симметрии, то эта ось является главной осью инерции для любой своей точки. Обратное утверждение не обязательно!

Если тело имеет плоскость симметрии, то любая ось перпендикулярная этой плоскости (например, ось Y) будет главной осью инерции тела для точки (например, точки О), в которой ось пересекает плоскость.

Если все центробежные моменты равны нулю, то есть 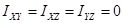, то каждая из координатных осей OX, OY, OZ является главной осью инерции для начала координат.

Осевые моменты инерции тела относительно главных осей инерции называются главными моментами инерции (например, ).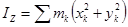

Главные оси инерции, построенные для центра масс тела, называются главными центральными осями инерции тела (на рисунке - это оси ).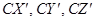

Если тело имеет ось симметрии, то эта ось является одной из главных центральных осей инерции (на рисунке - ось CZ).

Если тело имеет плоскость симметрии, то ось перпендикулярная этой плоскости и проходящая через центр масс также является главной центральной осью инерции (на рисунке - ось CY').

12.2.7 Теорема о движении центра масс системы:

Произведение массы системы на ускорение ее центра масс равно геометрической сумме всех действующих внешних сил, то есть центр масс системы движется как материальная точка, масса которой равна массе всей системы и к которой приложены все внешние силы, действующие на систему.

.

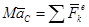Следствие - Закон сохранения движения центра масс: Если главный вектор всех внешних сил действующих на систему равен нулю, то центр масс этой системы находится в покое или движется равномерно и прямолинейно.

.

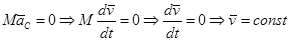Работа силы

13.1.1Элементарной работой силы, приложенной к точке называется скалярная величина равная скалярному произведению вектора силы и вектора перемещения точки приложения силы.

,

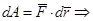
где 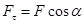- силы на направление движения;

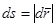- модуль вектора перемещения.

.

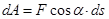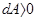, если ;

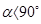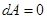, если (сила перпендикулярна перемещению);

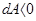, если .

Так как проекции 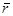на координатные оси равны

,

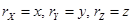то можно получить аналитическое выражение для элементарной работы:

.

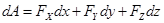13.1.2 Работа силы на любом конечном перемещении равна криволинейному интегралу от элементарной работы

;

;

.

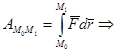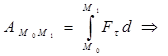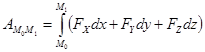Если 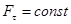, то .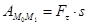

Если 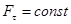, а точка движется прямолинейно, то .

.

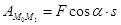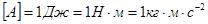13.1.3 Работа силы тяжести[1]

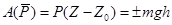
Тело падает под действием силы тяжести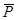

Тело поднимают вверх другой силой, преодолевая силу тяжести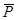

Работа силы тяжести не зависит от траектории движения тела, а определяется его начальным и конечным положением

13.1.4 Работа силы трения [1]

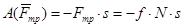
Работа силы трения всегда отрицательна, так как направлена в сторону противоположную движению тела по поверхности, и зависит от траектории движения тела.

 

13.1.5 Работа силы упругости [1]

,

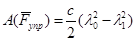где 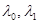- начальная и конечная деформация пружины (её удлинение или сжатие), см;

с - коэффициент жесткости пружины, Н/м.

Работа силы упругости зависит лишь от начального и конечного положения точки приложения силы упругости .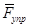

Силы, работа которых не зависит от траектории движения их точки приложения, называются потенциальными. Сила тяжести и сила упругости - потенциальные силы. Сила трения не потенциальная сила.

 

<28293031323334>

---

Дата добавления: 2016-01-29; просмотров: 5116;

---