Количество движения точки и системы. Импульс силы
14.1.1 Количеством движения точки называется векторная величина равная произведению массы точки на ее скорость
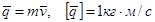 .
.
Вектор количества движения направлен также как и вектор скорости.
14.1.2 Количеством движения системы называется векторная величина равная векторной сумме (главному вектору) количеств движения всех точек системы
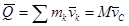 ,
,
где М - масса системы;
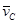 - скорость центра масс системы.
- скорость центра масс системы.
Количество движения системы равно произведению ее массы на скорость центра масс. Если тело движется так, что центр его масс остается неподвижным, например, ось вращения системы проходит через центр масс, то 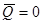 . Количество движения системы характеризует поступательную часть ее движения.
. Количество движения системы характеризует поступательную часть ее движения.
14.1.3 Элементарным импульсом силы называется векторная величина 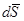 равная произведению силы
равная произведению силы 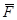 на элемент времени
на элемент времени 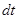
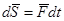 .
.
Направлен вектор 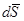 также как и вектор силы
также как и вектор силы 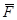 и характеризует действие силы за промежуток времени
и характеризует действие силы за промежуток времени 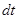 .
.
Импульс силы за некоторый конечный промежуток времени tравен интегралу от элементарного импульса
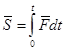 /
/
Если 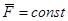 , то
, то 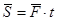 .
.
Проекции импульса на оси декартовых координат равны
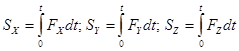 .
.
14.1.4 Теорема об изменении количества движения точки: Изменение количества движения точки за некоторый промежуток времени равно геометрической сумме импульсов всех действующих на точку сил за этот промежуток времени.
В дифференциальной форме:
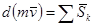 .
.
В интегральной форме:
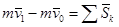 .
.
В проекциях на оси декартовых координат:
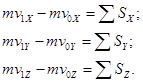
Теорема используется для решения первой и второй задач динамики.
14.1.6 Теорема об изменении количества движения системы: Изменение количества движения системы за некоторый промежуток времени равно сумме импульсов действующих на систему внешних сил за этот промежуток времени.
В дифференциальной форме:
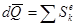 .
.
В интегральной форме:
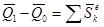 .
.
В проекциях на оси декартовых координат:
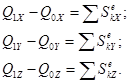
Следствие - Закон сохранения количества движения системы: Если сумма всех внешних сил действующих на систему равна нулю, то вектор количества движения системы постоянен по модулю и направлению, т.е.
при 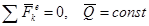 .
.
В проекциях на оси декартовых координат:
при 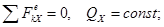
при 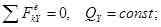
при 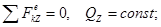
o 14.2 Момент количества движения (кинетический момент)
 14.2.1 Моментом количества движения (кинетическим моментом) точки А относительно центра О называется вектор
14.2.1 Моментом количества движения (кинетическим моментом) точки А относительно центра О называется вектор 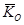 равный векторному произведению радиуса вектора
равный векторному произведению радиуса вектора 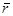 и вектора количества движения точки А
и вектора количества движения точки А 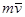
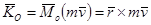 ;
;
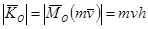 .
.
Кинетическим моментом относительно оси проходящей через очку О называется проекция кинетического момента относительно точки О на эту ось
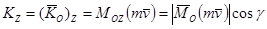 .
.
Теоремы 1, 2 об изменении кинетического момента точки: Производная по времени от кинетического момента точки, взятого относительно какого либо центра О (оси OZ), равна геометрической (алгебраической) сумме моментов действующих на эту точку сил относительно центра О (оси OZ).
1) 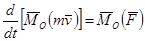 ;
;
2) 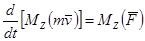 .
.
Следствия 1, 2:
– Если 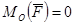 , то
, то 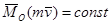 ;
;
2) Если 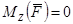 , то
, то 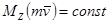 .
.
14.2.2 Кинетическим моментом системы относительно центра О называется векторная величина равная геометрической сумме моментов количества движения всех точек системы относительно этого центра
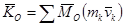 .
.
Кинетическим моментом системы относительно оси Z называется алгебраическая сумма кинетических моментов всех его точек относительно этой оси

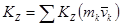
Дата добавления: 2016-01-29; просмотров: 1758;
