Аналитическим, т.е. исходя из теории изучаемой взаимосвязи;

3) экспериментальным.

При изучении зависимости между двумя признаками графический метод подбора вида уравнения регрессии достаточно нагляден. Он основан на поле корреляции. Основные типы кривых, используемые при количественной оценке связей, представлены на рис. 1.1:

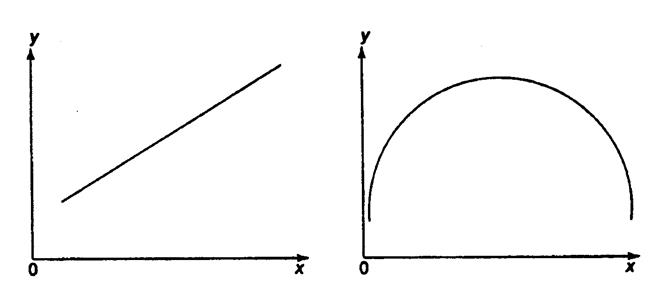
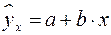
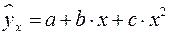
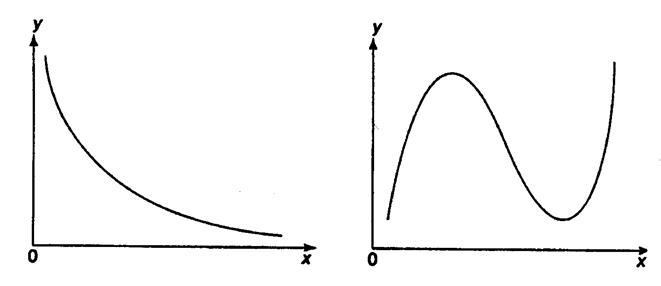
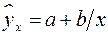
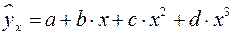
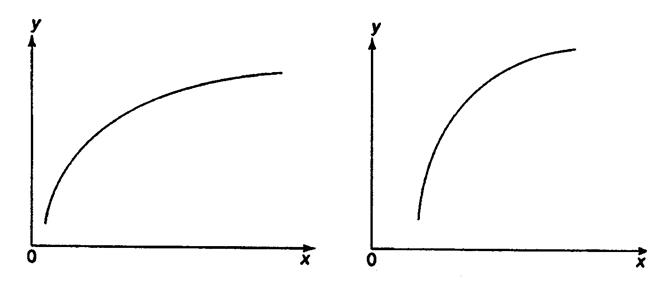
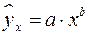
Рис. 1.1. Основные типы кривых, используемые при

количественной оценке связей между двумя переменными.

Значительный интерес представляет аналитический метод выбора типа уравнения регрессии. Он основан на изучении материальной природы связи исследуемых признаков.

При обработке информации на компьютере выбор вида уравнения регрессии обычно осуществляется экспериментальным методом, т. е. путем сравнения величины остаточной дисперсии 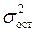, рассчитанной при разных моделях.

Если уравнение регрессии проходит через все точки корреляционного поля, что возможно только при функциональной связи, когда все точки лежат на линии регрессии 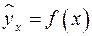, то фактические значения результативного признака совпадают с теоретическими 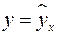, т.е. они полностью обусловлены влиянием фактора 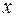. В этом случае остаточная дисперсия .

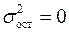В практических исследованиях, как правило, имеет место некоторое рассеяние точек относительно линии регрессии. Оно обусловлено влиянием прочих, не учитываемых в уравнении регрессии, факторов. Иными словами, имеют место отклонения фактических данных от теоретических 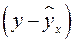. Величина этих отклонений и лежит в основе расчета остаточной дисперсии:

.

Чем меньше величина остаточной дисперсии, тем меньше влияние не учитываемых в уравнении регрессии факторов и тем лучше уравнение регрессии подходит к исходным данным.

Считается, что число наблюдений должно в 7-8 раз превышать число рассчитываемых параметров при переменной . Это означает, что искать линейную регрессию, имея менее 7 наблюдений, вообще не имеет смысла. Если вид функции усложняется, то требуется увеличение объема наблюдений, ибо каждый параметр при должен рассчитываться хотя бы по 7 наблюдениям. Значит, если мы выбираем параболу второй степени , то требуется объем информации уже не менее 14 наблюдений.