Парная регрессия и корреляция. Парная регрессия представляет собой регрессию между двумя переменными – и , т

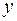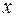Парная регрессия представляет собой регрессию между двумя переменными – и , т. е. модель вида:

,

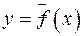где 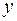– зависимая переменная (результативный признак); 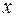– независимая, или объясняющая, переменная (признак-фактор). Знак «^» означает, что между переменным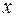и и 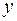нет строгой функциональной зависимости, поэтому практически в каждом отдельном случае величина 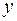складывается из двух слагаемых:

,

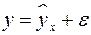где 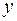– фактическое значение результативного признака; 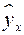– теоретическое значение результативного признака, найденное исходя из уравнения регрессии; 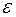– случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии.

Случайная величина 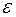называется также возмущением. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения. Ее присутствие в модели порождено тремя источниками: спецификацией модели, выборочным характером исходных данных, особенностями измерения переменных.

От правильно выбранной спецификации модели зависит величина случайных ошибок: они тем меньше, чем в большей мере теоретические значения результативного признака 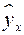, подходят к фактическим данным .

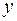К ошибкам спецификации относятся неправильный выбор той или иной математической функции для и недоучет в уравнении регрессии какого-либо существенного фактора, т. е. использование парной регрессии вместо множественной.

Наряду с ошибками спецификации могут иметь место ошибки выборки, которые имеют место в силу неоднородности данных в исходной статистической совокупности, что, как правило, бывает при изучении экономических процессов. Если совокупность неоднородна, то уравнение регрессии не имеет практического смысла. Для получения хорошего результата обычно исключают из совокупности единицы с аномальными значениями исследуемых признаков. И в этом случае результаты регрессии представляют собой выборочные характеристики.

Использование временной информации также представляет собой выборку из всего множества хронологических дат. Изменив временной интервал, можно получить другие результаты регрессии.

Наибольшую опасность в практическом использовании методов регрессии представляют ошибки измерения. Если ошибки спецификации можно уменьшить, изменяя форму модели (вид математической формулы), а ошибки выборки – увеличивая объем исходных данных, то ошибки измерения практически сводят на нет все усилия по количественной оценке связи между признаками.

Особенно велика роль ошибок измерения при исследовании на макроуровне. Так, в исследованиях спроса и потребления в качестве объясняющей переменной широко используется «доход на душу населения». Вместе с тем, статистическое измерение величины дохода сопряжено с рядом трудностей и не лишено возможных ошибок, например, в результате наличия скрытых доходов.

Предполагая, что ошибки измерения сведены к минимуму, основное внимание в эконометрических исследованиях уделяется ошибкам спецификации модели.

В парной регрессии выбор вида математической функции 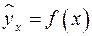может быть осуществлен тремя методами:

Графическим;