Ускорение при движении тела по окружности с постоянной по модулю скоростью (центростремительное ускорение)

При равномерном вращении по окружности модуль скорости υ движения тела не изменяется, но направление скорости изменяется непрерывно. Следовательно, данное движение — движение с ускорением. Оно характеризует быстроту изменения скорости по направлению.

По определению среднего ускорения ha⃗ i=Δυ⃗ Δt ha→i=Δυ→Δt . Треугольники ОАВ и BCD — равнобедренные (рис. 2). Углы при вершинах — одинаковые (как углы с соответственно перпендикулярными сторонами). Отсюда следует, что Δ ОАВ подобен Δ BCD.

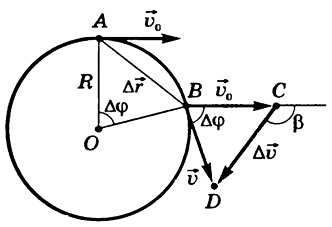
Рис. 2

Из подобия |Δυ⃗ |υ=|Δr⃗ |R⇒|Δυ⃗ |=υ|Δr⃗ |R |Δυ→|υ=|Δr→|R⇒|Δυ→|=υ|Δr→|R

Тогда hai=υR⋅|Δr⃗ |Δt hai=υR⋅|Δr→|Δt .

Мгновенное ускорение a=limΔt→0hai=υRlimΔt→0|Δr⃗ |Δt=υ2R a=limΔt→0hai=υRlimΔt→0|Δr→|Δt=υ2R .

β — угол между υ⃗ 0 υ→0 и Δυ⃗ (ha⃗ i) Δυ→(ha→i) — внешний по отношению к Δ BCD:

β=Δφ+180−Δφ2=90+Δφ2. β=Δφ+180−Δφ2=90+Δφ2.

При Δt → 0 угол Δφ → 0 и, следовательно, β → 90°. Перпендикуляром к касательной к окружности является радиус. Следовательно, a⃗ a→ направлено по радиусу к центру и поэтому называется центростремительным ускорением:

a=υ2R. a=υ2R.

Модуль а = const, направление a⃗ a→ непрерывно изменяется (рис. 3). Поэтому данное движение не является равноускоренным.

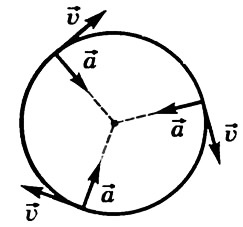
Рис. 3

Угловая скорость при вращении тела вокруг неподвижной точки

Угловой скоростью называют векторную величину, характеризующую быстроту вращения твердого тела, определяемую как приращение угла поворота тела за промежуток времени.

Рекомендуем

Примеры расчета угловой скорости

Рассмотрим бесконечно малый промежуток времени Δt → 0, за который твердое тело совершает поворот на бесконечно малый угол Δα вокруг мгновенной оси Ω (рисунок 3.2).

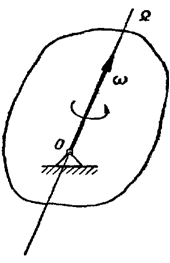
Рис. 3.2

Предел, к которому стремится отношение Δα / Δt, называется угловой скоростью твердого тела в рассматриваемый момент времени

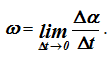
Угловая скорость является векторной величиной. Вектор угловой скорости ω может быть приложен к любой точке мгновенной оси и направлен в каждый момент времени по мгновенной оси Ω, так, чтобы, смотря навстречу этому вектору, видеть вращение тела происходящим против движения часовой стрелки.