СТА: Лекция №3 - Реализация и использование простейших АТД
Версия 2.0, 8 сентября 2013г.
(С) 2012-2013, Зайченко Сергей Александрович, к.т.н, ХНУРЭ, доцент кафедры АПВТ
Абстрактные типы данных (АТД)
Абстрактный тип данных (АТД) - математическая модель и совокупность определенных на ней операций, используемая при неформальном определении алгоритмов. АТД определяет набор действий, иначе говоря, интерфейс, независимый от конкретной реализации типа, для оперирования его значениями.
При рассуждении на уровне АТД реализация операций полностью скрыта. В литературе по классическим алгоритмам часто можно встретить описание в виде псевдокода - некоторой смеси программных инструкций и естественного языка, оперирующего данными с использованием АТД и свойственных им операций. Алгоритмы, определение которых ограничено в терминах операций над АТД, не зависят от конкретных реализаций.
АТД реализуется при помощи структур данных в конкретных языках программирования. Может существовать несколько реализаций АТД в виде структур данных, при этом реализация каждой из операций может характеризоваться различной производительностью. Благодаря единому набору операций, реализации АТД могут быть взаимозаменяемыми. Такой подход к организации обработки данных способствует улучшению модульности разрабатываемых программ. Модульность, в свою очередь, существенно упрощает проектирование, разработку и развитие программ.
К простейшим АТД относятся:
· список, или последовательность (list/sequence);
· стек (stack);
· очередь (queue);
· отображение (map);
· множество (set).
Операции АТД обычно разделаются на команды (command) и запросы (query). Операции-команды выполняют некоторые действия, которые изменяют внутреннее состояние объектов АТД, но не возвращают никакого результата. Операции-запросы, напротив, возвращают некоторое значение-результат, основанный на текущем состоянии объекта АТД, но при этом ни коим образом его не модифицируют. В названии операций-запросов обычно присутствуют типичные префиксы - GET, IS, TRY - что несвойственно операциям-командам. Операций АТД, одновременно являющихся и командами, и запросами принято избегать, поскольку они нарушают естественную логику и ухудшают восприятие алгоритмов и их реализаций.
Многие АТД обладают похожими друг на друга операциями. Например, содержимое любого АТД можно очистить (команда CLEAR), также можно определить пустоту содержимого АТД (запрос IS_EMPTY). Другие операции являются более специфическими для конкретного АТД (например, операция INTERSECT для множеств).
Аргументами операций АТД могут являться как элементарные типы данных, так и другие АТД или связанные с АТД вспомогательные элементы.
АТД “Список” ( “Последовательность” )
Список является наиболее распространенным в программировании абстрактным типом данных. Список представляет собой упорядоченную последовательность значений некоторого типа элементов. Длина списка - это количество содержащихся в нем элементов. Список, длина которого равна 0, называется пустым.
Списки предоставляют свободный доступ к своим элементам, различаемым по позиции. Список имеет начальную и конечную позицию. Позиция может быть также недействительной, что применяется для ситуаций, когда требуется указать на ее некорректность или отсутствие в списке. Какое именно данное используется в качестве позиции в конкретной реализации АТД на абстрактном уровне не играет роли, достаточно обеспечить возможность доступа к элементам через позиции, а также операции сравнения значений, играющих роль позиции.
К операциям, определяемых на модели списков, относятся:
· CLEAR( list ) - делает список пустым;
· IS_EMPTY( list ) : bool - определяет является ли список пустым;
· GET_LENGTH( list ) : int - возвращает длину списка;
· GET_NEXT( list, pos ): pos - возвращает следущую позицию после указанной;
· GET_PREV( list, pos ): pos - возвращает предыдущую позицию после указанной;
· GET_FIRST( list ): pos - возвращает первую позицию в списке;
· GET_LAST( list ) : pos - возвращает позицию в списке, следующую за последней;
· INSERT ( list, pos, value ) - вставляет значение в указанную позицию в списке, перемещая все элементы от поизции и далее в следующую более “высокую” позицию;
· RETREIVE ( list, pos ) : value - возвращает хранящееся в списке значение по указанной позиции;
· DELETE( list, pos ) - удалает из списка элемент, хранящийся по указанной позиции.
Подразумевается, что конкретная реализация алгоритмов заменит все типы и названия операций АТД на конкретные, которые отвечают ожидаемому поведению. Операции над последовательностями можно реализовать многими способами. Наиболее ожидаемыми будут реализации на основе рассмотренных ранее в курсе базовых структур данных - векторов и связных списков. Основную массу операций оформляют в виде функций, однако, в целях упрощения, вместо тривиальных функций можно использовать соответствующие очевидные выражения напрямую.
Если в качестве реализации АТД “список” выступает вектор, то в качестве значений-позиций используются индексы в массиве данных. Операции с позициями сводятся к простейшим числовым действиям. Значение -1 можно использовать как недействительную позицию.
В случае выбора связных списков в качестве структуры для реализации, роль значений-позиций будут играть адреса элементов-узлов. Операции с позициями в таком случае будут задействовать структурные связи из объекта-списка и объектов-узлов. Недействительная позиция в списке - нулевой адрес узла.
Ниже в виде таблиц представлены эквивалентные реализации операций АТД “список” для целых чисел, использующие рассмотренные ранее базовые структуры данных. Ранее реализованные функции не расписываются, а для новых указана полная реализация.
| Операция АТД “Список” | Реализация на основе векторов |
| CLEAR( list ) | v.m_nUsed = 0; |
| IS_EMPTY( list ) : bool | returnv.m_nUsed > 0; |
| GET_LENGTH( list ) : int | returnv.m_nUsed; |
| GET_NEXT( list, pos ): pos | returnpos + 1; |
| GET_PREV( list, pos ): pos | returnpos - 1; |
| GET_FIRST( list ): pos | return0; |
| GET_LAST( list ) : pos | returnv.m_nUsed; |
| INSERT ( list, pos, value ) | IntegerVectorInsertAt( v, pos, value ); |
| RETREIVE ( list, pos ) : value | returnv.m_pData[ pos ]; |
| DELETE( list, pos ) | IntegerVectorDeleteAt( v, pos ); |
| Операция АТД “Список” | Реализация на основе связных списков |
| CLEAR( list ) | IntegerListDestroy( l ); IntegerListInit( l ); |
| IS_EMPTY( list ) : bool | return! l.m_pFirst; |
| GET_LENGTH( list ) : int | intIntegerListGetLength ( constIntegerList & _l ) { intlength = 0; IntegerList::Node * pNode = _l.m_pFirst; while( pNode ) { ++ length; pNode = pNode->m_pNext; } returnlength; } |
| GET_NEXT( list, pos ): pos | returnpNode->m_pNext; |
| GET_PREV( list, pos ): pos | IntegerList::Node * IntegerListGetPrevNode ( constIntegerList & _l, IntegerList::Node * _pNode ) { assert( _pNode ); IntegerList::Node * prevNode = _l.m_pFirst; while( prevNode && prevNode->m_pNext != _pNode ) prevNode = prevNode->m_pNext; returnprevNode; } Для двусвязных список используем связь m_pPrev сразу. |
| GET_FIRST( list ): pos | return l.m_pFirst; |
| GET_LAST( list ) : pos | return nullptr; Связь l.m_pLast является последним значением, а не следующим за последним, как этого требует определение АТД |
| INSERT ( list, pos, value ) | IntegerListInsertAfter( l, pNode, value ); |
| RETRIEVE ( list, pos ) : value | returnpNode->m_value; |
| DELETE( list, pos ) | voidIntegerListDeleteNode ( IntegerList & _l, IntegerList::Node * _pNode ) { IntegerListDeleteBefore( _l, _pNode->m_pNext ); } Можно оптимизировать, если известен адрес предыдущего узла: IntegerListDeleteAfter( _l, _pPrevNode ); |
Предположим, требуется реализовать простейший алгоритм поиска интересующего значения в списке путем полного перебора. Ниже представлено описание данного алгоритма в виде псевдокода:
position FIND ( list myList, value v )
{
position p;
p = GET_FIRST( myList );
while( p < GET_LAST( myList ) )
{
if( RETRIEVE( myList, p ) == v )
return p;
p = GET_NEXT( myList, p );
}
returnINVALID_POSITION;
}
Далее демонстрируются оба варианта реализации алгоритма FIND, использующие предложенные выше фрагменты кода для каждой из операций АТД “список”. Соответствующие реализации инструкции из изначального псевдокода размещены в комментариях.
Реализация алгоритма на основе векторов выглядит следующим образом:
// position FIND( list myList, value v )
intfind ( const IntegerVector & _v, int _value )
{
// position p;
// p = GET_FIRST( myList );
intp = 0;
// while( p < GET_LAST( myList ) )
while ( p < _v.m_nUsed )
{
// if( RETRIEVE( myList, p ) == v )
// return p;
if( _v.m_pData[ p ] == _value )
returnp;
// p = GET_NEXT( myList, p );
++p;
}
// returnINVALID_POSITION;
return-1;
}
Следующим образом реализуется альтернативная версия на основе связных списков:
// position FIND( list myList, value v )
IntegerList::Node * find ( const IntegerList & _l, int _value )
{
// position p;
// p = GET_FIRST( myList );
IntegerList::Node * p = _l.m_pFirst;
// while( p < GET_LAST( myList ) )
while ( p )
{
// if( RETRIEVE( myList, p ) == v )
// return p;
if( p->m_value == _value )
returnp;
// p = GET_NEXT( myList, p );
p = p->m_pNext;
}
// returnINVALID_POSITION;
return nullptr;
}
Как видно из приведенного примера, элементы изначального неформально описанного алгоритма четко прослеживаются в коде с использованием каждой из реализаций АТД.
Приведем еще один пример алгоритма, определенного в терминах операций АТД - алгоритм удаления из списка повторяющихся элементов. В виде псевдокода потребуются следующие инструкции:
voidPURGE ( list myList )
{
position p, q;
p = GET_FIRST( myList );
while( p < GET_LAST( myList ) )
{
q = GET_NEXT( myList, p );
while( q < GET_LAST( myList ) )
{
if( RETRIEVE( myList, p ) == RETRIEVE( myList, q ) )
DELETE( myList, q );
Else
q = GET_NEXT( myList, q );
}
p = GET_NEXT( myList, p );
}
}
Реализация на основе векторов:
#include “integer_vector.hpp”
// voidPURGE ( list myList )
voidpurge ( IntegerVector & _v )
{
// p = GET_FIRST( myList );
intp = 0;
// while ( p < GET_LAST( myList ) )
while( p < _v.m_nUsed )
{
// q = GET_NEXT( myList, p );
int q = p + 1;
// while ( q < GET_LAST( myList ) )
while( q < _v.m_nUsed )
{
// if ( RETRIEVE( myList, p ) == RETRIEVE( myList, q ) )
// DELETE( myList, q );
// else
// q = GET_NEXT( myList, q );
if( _v.m_pData[ p ] == _v.m_pData[ q ] )
IntegerVectorDeleteAt( _v, q );
Else
++q;
}
// p = GET_NEXT( myList, p );
++p;
}
}
Реализация на основе связных списков:
#include “integer_list.hpp”
// voidPURGE ( list myList )
voidpurge ( IntegerList & _l )
{
// p = GET_FIRST( myList );
IntegerList::Node * p = _l.m_pFirst;
// while ( p < GET_LAST( myList ) )
while( p )
{
// q = GET_NEXT( myList, p );
IntegerList::Node * q = p->m_pNext;
IntegerList::Node * prevQ = p;
// while ( q != GET_LAST( myList ) )
while( q )
{
// if ( RETRIEVE( myList, p ) == RETRIEVE( myList, q ) )
// DELETE( myList, q );
// else
// q = GET_NEXT( myList, q );
if( p->m_value == q->m_value )
{
IntegerListDeleteAfter( _l, prevQ );
q = prevQ->m_pNext;
}
Else
{
prevQ = q;
q = q->m_pNext;
}
}
// p = GET_NEXT( myList, p );
p = p->m_pNext;
}
}
Поскольку производительность каждой операции может различаться между реализациями (в частности, операция удаления элемента из списка в произвольной позиции), из второго примера очевидно, что быстродействие алгоритма существенно зависит от свойств выбранной в качестве основы структуры данных
АТД “Стек”
АТД “Стек” представляет собой набор данных, доступ, вставка и удаление элементов из которого может происходить только с конца. Стек организовывается по принципу LIFO (Last In - First Out). Чаще всего стек сравнивают со стопкой тарелок - тарелка сверху, которую поставили последней, будет использоваться первой, а тарелка на дне стопки, которую поставили первой, будет доступна только тогда, когда снимут все остальные тарелки. В литературе стек иногда называют магазином, что соответствует аналогии с патронами для огнестрельного оружия - первый выстрел использует патрон, помещенный в магазин последним.
При неформальном анализе стек принято изображать в вертикальной форме. При этом первое помещенное значение попадает на дно стека, а последнее находится на вершине стека. При добавлении очередного значения вершина растет. При удалении - уменьшается. В пустом стеке вершина и дно совпадают.
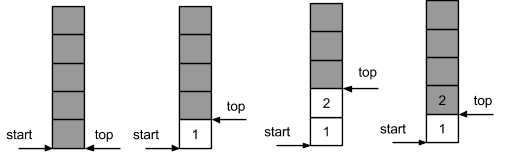
Максимальный размер стека, т.е. число элементов, которые можно в нем разместить, может быть ограниченным или неограниченным. Если размер ограничен, удобнее всего реализовывать стек при помощи простейшего массива. Если размер неограничен, стек не трудно выразить через уже известные структуры данных - вектора и списки.
Стеки предполагают наличие следующего набора абстрактных операций:
· CLEAR( stack ) - делает стек пустым;
· IS_EMPTY( stack ) : bool - определяет является ли стек пустым;
· PUSH ( stack, value ) - помещает новое значение на вершину стека;
· POP ( stack ) - удаляет значение с вершины стека;
· TOP ( stack ) : value - возвращает значение на вершине стека;
Если стек имеет ограниченный размер, к перечисленному выше набору операций добавляется:
· IS_FULL( stack ) : bool - определяет является ли стек полностью заполненным
Иногда в литературе можно встретить определение операции POP, которое помимо удаления значения с вершины стека также возвращает удаленное только что значение. Такой стиль не рекомендуется, поскольку он нарушает принцип разделения всех операций на команды и запросы.
Ниже приведен заголовочный файл, отражающий операции со стеком в виде объявлений функций. Отметим, что структура объявляется лишь предварительно, а ее содержимое в данный момент не указывается. Это способствует улучшению модульности программ, поскольку представляется возможным создавать программный код, использующий стек, не задумываясь ежеминутно о принципах его реализации. Такой подход также позволяет полностью скрыть внутреннюю структуру реализации от случайного разрушения при прямых манипуляциях с полями в клиентском коде, и позволяет ограничить интерфейс к структуре только предоставленными открытыми операциями. Сама структура, за которой стоит реальная реализация, используется в клиентском коде исключительно как описатель (handle). Описатели предоставляются при создании объекта и в дальнейшем используются в операциях для его идентификации, т.е., чтобы отличить один объект от другого. По такому принципу устроено большое количество существующих интерфейсов прикладного программирования (API), выкристаллизовавшихся до начала массовой популяризации принципов объектно-ориентированного программирования (например, Windows API, изучаемый в курсе системного программирования).
integer_stack.hpp
#ifndef _INTEGER_STACK_HPP_
#define _INTEGER_STACK_HPP_
structIntegerStack;
IntegerStack * IntegerStackCreate ();
voidIntegerStackDestroy ( IntegerStack * _pStack );
voidIntegerStackClear ( IntegerStack & _stack );
boolIntegerStackIsEmpty ( constIntegerStack & _stack );
boolIntegerStackIsFull ( constIntegerStack & _stack );
voidIntegerStackPush ( IntegerStack & _stack, int _value );
voidIntegerStackPop ( IntegerStack & _stack );
intIntegerStackTop ( constIntegerStack & _stack );
#endif // _INTEGER_STACK_HPP_
На основе приведенных выше определений представляется возможным написать простую программу, которая проверяет корректность его работы. Отметим, что такая программа успешно компилируется, однако не может быть скомпонована до появления одной из реализаций:
#include "integer_stack.hpp"
#include <cassert>
intmain ()
{
// Создаем новый стек, получаем описатель
IntegerStack * pStack = IntegerStackCreate();
// Помещаем 3 значения в стек
IntegerStackPush( * pStack, 1 );
IntegerStackPush( * pStack, 2 );
IntegerStackPush( * pStack, 3 );
// Убеждаемся, что на вершине стека значение 3
assert( IntegerStackTop( * pStack ) == 3 );
// Удалаем два значения из стека
IntegerStackPop( * pStack );
IntegerStackPop( * pStack );
// Ожидаем, что на вершине останется значение 1
assert( IntegerStackTop( * pStack ) == 1 );
// Удаляем последнее значение из стека
IntegerStackPop( * pStack );
// Стек должен быть пуст
assert( IntegerStackIsEmpty( * pStack ) );
// Уничтожаем объект-стек
IntegerStackDestroy( pStack );
}
Реализация стека на основе вектора или связного списка тривиальна, поскольку реализация всех операций сводится к ограничению набора существующих операций, нежели к созданию принципиально новой функциональности. Обе реализации можно подключать к проекту в паре с одним и тем же заголовочным файлом (только не одновременно - это вызовет ошибки компоновки из-за дупликации функций с одинаковыми именами).
Ниже приведена реализация стека через вектор:
integer_stack_vector_impl.cpp
#include "integer_stack.hpp"
#include "integer_vector.hpp"
structIntegerStack
{
// Реализуем стек через вектор
IntegerVector m_Vector;
};
IntegerStack * IntegerStackCreate ()
{
// Создаем объект-стек в динамической памяти,
// т.к. только здесь известен настоящий тип
IntegerStack * pStack = newIntegerStack;
// Инициализируем внутренний объект-вектор
IntegerVectorInit( pStack->m_Vector );
// Возвращаем указатель на реальный стек,
// он будет использоваться в клиентском коде как описатель
returnpStack;
}
voidIntegerStackDestroy ( IntegerStack * _pStack )
{
// Уничтожаем внутренний объект-вектор
IntegerVectorDestroy( _pStack->m_Vector );
// Уничтожаем объект-стек, т.к. только мы знаем его настоящий тип
delete_pStack;
}
voidIntegerStackClear ( IntegerStack & _stack )
{
// Сбрасываем счетчик используемых ячеек вектора
_stack.m_Vector.m_nUsed = 0;
}
boolIntegerStackIsEmpty ( constIntegerStack & _stack )
{
// Стек пуст, когда пуст вектор
return! _stack.m_Vector.m_nUsed;
}
boolIntegerStackIsFull ( constIntegerStack & _stack )
{
// Такой стек в теории не переполняется никогда!
return false;
}
voidIntegerStackPush ( IntegerStack & _stack, int_value )
{
// Поместить в стек = Поместить в конец внутреннего вектора
IntegerVectorPushBack( _stack.m_Vector, _value );
}
voidIntegerStackPop ( IntegerStack & _stack )
{
// Удалить с вершины стека = Удалить с конца внутреннего вектора
IntegerVectorPopBack( _stack.m_Vector );
}
intIntegerStackTop ( constIntegerStack & _stack )
{
// Вершина стека - последняя позиция в векторе
return_stack.m_Vector.m_pData[ _stack.m_Vector.m_nUsed - 1 ];
}
Далее следует альтернативная реалиация на основе связных списков:
integer_stack_list_impl.cpp
#include "integer_stack.hpp"
#include "integer_list.hpp"
structIntegerStack
{
// Реализуем стек через связный список
IntegerList m_List;
};
IntegerStack * IntegerStackCreate ()
{
// Создаем объект-стек в динамической памяти,
// т.к. только здесь известен настоящий тип
IntegerStack * pStack = newIntegerStack;
// Инициализируем внутренний объект-список
IntegerListInit( pStack->m_List );
// Возвращаем указатель на реальный стек,
// он будет использоваться в клиентском коде как описатель
returnpStack;
}
voidIntegerStackDestroy ( IntegerStack * _pStack )
{
// Уничтожаем внутренний объект-список
IntegerListDestroy( _pStack->m_List );
// Уничтожаем объект-стек, т.к. только мы знаем его настоящий тип
delete_pStack;
}
void IntegerStackClear ( IntegerStack & _stack )
{
// Для списка очистка равносильна уничтожению
IntegerListDestroy( _stack.m_List );
}
boolIntegerStackIsEmpty ( constIntegerStack & _stack )
{
// Стек пуст, когда пуст список
returnIntegerListIsEmpty( _stack.m_List );
}
boolIntegerStackIsFull ( constIntegerStack & _stack )
{
// Такой стек в теории не переполняется никогда!
return false;
}
voidIntegerStackPush ( IntegerStack & _stack, int_value )
{
// Поместить в стек = Поместить в конец внутреннего списка
IntegerListPushBack( _stack.m_List, _value );
}
voidIntegerStackPop ( IntegerStack & _stack )
{
// Удалить с вершины стека = Удалить с конца внутреннего списка
IntegerListPopBack( _stack.m_List );
}
intIntegerStackTop ( constIntegerStack & _stack )
{
// Вершина стека - последний узел списка
return_stack.m_List.m_pLast->m_value;
}
Приведенная выше тестовая программа будет функционировать одинаково как при первой, так и при второй реализации стека. Могут отличаться лишь показатели производительности. Например, вызывает сомнения реализация операции POP на односвязных списках, поскольку это потребует просматривать список с первого до последнего узла. Если делать выбор при реализации стека в пользу связных списков, следует предпочесть двусвязный вариант.
Иногда задача предполагает совершенно четкое ограничение вернего размера стека, и в таком случае использование динамических структур данных может быть не оправдано. Реализация на основе простейшего однажды выделяемого массива будет наиболее эффективной.
Основное отличие от предыдущих реализаций состоит в том, что размер стека нужно передавать в момент его создания. Это повлияет на разработанную тестовую программу необходимостью указать конкретный размер в вызове IntegerStackCreate. Соответственно, в заголовочный файл следует дополнительно внести следующий прототип:
IntegerStack * IntegerStackCreate ( int_fixedSize );
Также, при помещении очередного значения в стек, потребуется проверка наличия сводобного места, т.е. защита от переполнения (stack overflow).
Ниже представлена реализация операций стека на основе массива фиксированного размера:
integer_stack_array_impl.cpp
#include "integer_stack.hpp"
#include <cassert>
structIntegerStack
{
// Указатель на начало блока данных
int* m_pData;
// Вершина стека - указывает на ячейку в блоке данных для следующей записи
int* m_pTop;
// Общий размер стека
intm_Size;
};
IntegerStack * IntegerStackCreate ( int_fixedSize )
{
// Создаем объект-стек в динамической памяти,
// т.к. только здесь известен настоящий тип
IntegerStack * pStack = newIntegerStack;
// Заполняем поля:
// - блок для хранения данных выделяем динамически (m_pData)
// - изначальное положение вершины - нулевая позиция (m_pTop)
// - запоминаем размер выделенного блока
pStack->m_pData = new int[ _fixedSize ];
pStack->m_pTop = pStack->m_pData;
pStack->m_Size = _fixedSize;
// Возвращаем указатель на реальный стек,
// он будет использоваться в клиентском коде как описатель
returnpStack;
}
voidIntegerStackDestroy ( IntegerStack * _pStack )
{
// Уничтожаем внутренний блок данных
delete[] _pStack->m_pData;
// Уничтожаем объект-стек, т.к. только мы знаем его настоящий тип
delete_pStack;
}
voidIntegerStackClear ( IntegerStack & _stack )
{
// Сбрасываем указатель на вершину в начальное состояние
_stack.m_pTop = _stack.m_pData;
}
voidIntegerStackPush ( IntegerStack & _stack, int_value )
{
// В стеке должно быть достаточно места
assert( ! IntegerStackIsFull( _stack ) );
// Записываем новое данное в вершину
* _stack.m_pTop = _value;
// Повышаем указатель на вершину на 1 ячейку
++ _stack.m_pTop;
}
voidIntegerStackPop ( IntegerStack & _stack )
{
// В стеке должно быть хотя бы одно данное
assert( ! IntegerStackIsEmpty( _stack ) );
// Опускаем указатель вершину на одну ячейку
-- _stack.m_pTop;
}
intIntegerStackTop ( constIntegerStack & _stack )
{
// В стеке должно быть хотя бы одно данное
assert( ! IntegerStackIsEmpty( _stack ) );
// Считываем значение, находящееся под указателем-вершиной
return* ( _stack.m_pTop - 1 );
}
boolIntegerStackIsEmpty ( constIntegerStack & _stack )
{
// Стек пуст, когда указатели на начало блока и вершину совпадают
return_stack.m_pData == _stack.m_pTop;
}
boolIntegerStackIsFull ( constIntegerStack & _stack )
{
// Стек полон, когда расстояние между вершиной и началом блока равно размеру стека
return( _stack.m_pTop - _stack.m_pData ) == _stack.m_Size;
}
АТД “Очередь”
АТД “Очередь” (queue) - это набор данных, организованный таким образом, что вставка нового элемента производится только с конечной ячейки, а удаление - только с начальной. Очередь работает по принципу FIFO (First In - First Out), что соответствует общепринятому понятию очереди в жизни, например, возле кассы в супермаркете.
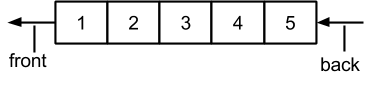
Также как и стек, очередь может быть ограниченного и неограниченного размера в зависимости от потребностей решаемой задачи.
Очередь предполагает наличие следующих абстрактных операций:
· CLEAR( queue ) - делает очередь пустой;
· IS_EMPTY( queue ) : bool - определяет является ли очередь пустой;
· IS_FULL( queue ) : bool - определяет является ли очередь полностью заполненной (что имеет смысл только для очередей ограниченного размера);
· PUSH ( queue , value ) - помещает новое значение в конец очереди;
· POP ( queue ) - удаляет значение с начала очереди;
· FRONT ( queue ) : value - возвращает значение в начале очереди.
Пользуясь выбранным ранее стилем реализации, интерфейс для работы с очередью можно описать в виде заголовочного файла, скрывающего внутреннюю структуру:
integer_queue.hpp
#ifndef _INTEGER_QUEUE_HPP_
#define _INTEGER_QUEUE_HPP_
structIntegerQueue;
IntegerQueue * IntegerQueueCreate ();
voidIntegerQueueDestroy ( IntegerQueue * _pQueue );
voidIntegerQueueClear ( IntegerQueue & _queue );
boolIntegerQueueIsEmpty ( constIntegerQueue & _queue );
boolIntegerQueueIsFull ( constIntegerQueue & _queue );
voidIntegerQueuePush ( IntegerQueue & _queue, int_value );
voidIntegerQueuePop ( IntegerQueue & _queue );
intIntegerQueueFront ( constIntegerQueue & _queue );
#endif // _INTEGER_QUEUE_HPP_
Очередь неограниченного размера легко реализуется при помощи односвязных списков. Выбор вектора в качестве основы очереди назвать удачным нельзя, поскольку очередь часто использует неэффективую для векторов операцию удаления элемента из начала последовательности. Реализация же на основе односвязных списков прекрасно подходит для всех операций:
integer_queue_list_impl.cpp
#include "integer_queue.hpp"
#include "integer_list.hpp"
#include <cassert>
structIntegerQueue
{
// Реализуем очередь через связный список
IntegerList m_List;
};
IntegerQueue * IntegerQueueCreate ()
{
// Создаем объект-очередь динамической памяти,
// т.к. только здесь известен настоящий тип
IntegerQueue * pNewQueue = newIntegerQueue;
// Инициализируем внутренний объект-список
IntegerListInit( pNewQueue->m_List );
// Возвращаем указатель на реальную очередь,
// он будет использоваться в клиентском коде как описатель
returnpNewQueue;
}
voidIntegerQueueDestroy ( IntegerQueue * _pQueue )
{
// Уничтожаем внутренний объект-список
IntegerListDestroy( _pQueue->m_List );
// Уничтожаем объект-очередь, т.к. только мы знаем его настоящий тип
delete_pQueue;
}
voidIntegerQueueClear ( IntegerQueue & _queue )
{
// Очистка списка равносильна его уничтожению
IntegerListDestroy( _queue.m_List );
}
boolIntegerQueueIsEmpty ( constIntegerQueue & _queue )
{
// Очередь пуста, когда пуст внутренний список
returnIntegerListIsEmpty( _queue.m_List );
}
boolIntegerQueueIsFull ( constIntegerQueue & _queue )
{
// Такая очередь в теории никогда не переполнится
return false;
}
voidIntegerQueuePush ( IntegerQueue & _queue, int_value )
{
// Помещение элемента в очередь = добавление элемента в конец списка
IntegerListPushBack( _queue.m_List, _value );
}
voidIntegerQueuePop ( IntegerQueue & _queue )
{
// Удаление элемента из очереди = удаление элемента с начала списка
assert( ! IntegerQueueIsEmpty( _queue ) );
IntegerListPopFront( _queue.m_List );
}
intIntegerQueueFront ( const IntegerQueue & _queue )
{
// Начало очереди в начале списка
assert( ! IntegerQueueIsEmpty( _queue ) );
return_queue.m_List.m_pFirst->m_value;
}
Используя реализованную функциональность, решим следующую задачу: пользователь вводит последовательность целых чисел, а программа, начиная с 3-го числа, дублирует ввод с отставанием на 2 элемента. Т.е., при вводе последовательности “1 2 3 4 5” программа должна вывести поэлементно последовательность “1 2 3”, начиная с момента ввода числа “3”.
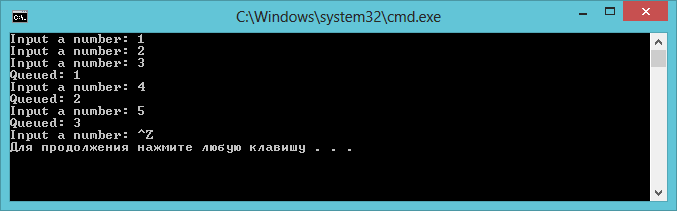
Ниже приведен исходный код данной программы:
#include "integer_queue.hpp"
#include <iostream>
intmain ()
{
IntegerQueue * pQueue = IntegerQueueCreate();
intdelayCounter = 2;
while( std::cin )
{
std::cout << "Input a number: ";
inttemp;
std::cin >> temp;
if( std::cin )
{
IntegerQueuePush( * pQueue, temp );
if( delayCounter > 0 )
-- delayCounter;
Else
{
std::cout << "Queued: " << IntegerQueueFront( * pQueue ) << std::endl;
IntegerQueuePop( * pQueue );
}
}
Else
break;
}
IntegerQueueDestroy( pQueue );
}
Если задача предполагает ограничение размера очереди, удачной структурой является циклический массив. Примем условно, что элементом массива, следующим за последним, является начальный элемент. Предполагается хранение индексов для помещения в условный конец очереди (m_BackIndex) и для изъятия из условного начала очереди (m_FrontIndex). При помещении нового элемента индекс конца увеличивается с учетом возможного закицливания. Аналогично, при изъятии элемента, увеличивается индекс начала очереди. В результате работы индексы могут как бы “перехлестнуться”.
Количество хранимых элементов можно определить по разнице индексов, при этом следует учесть возможное “перехлестывание”. Однако, чтобы отличить пустую очередь от очереди, заполненной на 100%, следует зарезервировать дополнительную ячейку. Т.е., когда требуется очередь, скажем, из 5 элементов, следует выделить блок из 6 ячеек. В результате, когда очередь будет полна, должна быть сводобна ровно 1 ячейка.
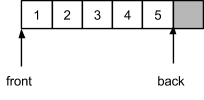
Ниже приведены примеры состояния циклического массива в результате воздействия. В пустой очереди индексы начала и конца совпадут:

После добавления элемента в очередь индекс конца будет двигаться, а начала - стоять на месте:
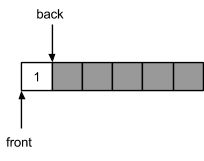
Элементы можно будет добавлять до достижения максимально разрешенного числа хранимых ячеек, что соответствует размеру выделенного блока минус 1:
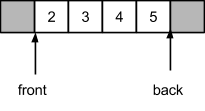
Если затем начать изымать элементы из очереди, двигаться вправо будет индекс начала, а индекс конца останется на месте:
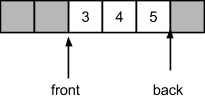
Поскольку часть места освобождена, можно продолжать добавлять элементы в конец очереди. Это может привести к “перехлестыванию” индексов, т.е., когда абсолютное значение индекса конца очереди будет меньшим абсолютного значения индекса начала очереди.
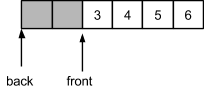

Ситуация может вернуться в обратную сторону, если вновь изъять несколько элементов:
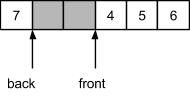
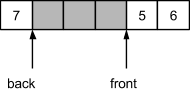
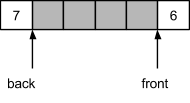

За счет подмены индексов при выходе за границу массива, достигается иллюзия циклической структуры. Ниже представлена реализация данного подхода:
integer_queue_cyclic_array_impl.cpp
#include "integer_queue.hpp"
#include <cassert>
structIntegerQueue
{
int* m_pData;
intm_Size;
intm_FrontIndex;
intm_BackIndex;
};
IntegerQueue * IntegerQueueCreate ( int_fixedSize )
{
assert( _fixedSize > 0 );
IntegerQueue * pNewQueue = newIntegerQueue;
pNewQueue->m_Size = _fixedSize + 1;
pNewQueue->m_pData = new int[ pNewQueue->m_Size ];
IntegerQueueClear( * pNewQueue );
returnpNewQueue;
}
voidIntegerQueueDestroy ( IntegerQueue * _pQueue )
{
delete[] _pQueue->m_pData;
delete_pQueue;
}
voidIntegerQueueClear ( IntegerQueue & _queue )
{
_queue.m_FrontIndex = _queue.m_BackIndex = 0;
}
intIntegerQueueSize ( constIntegerQueue & _queue )
{
// |-|-|-|-|-|-| |-|-|-|-|-|-|
// F B B F
return( _queue.m_FrontIndex <= _queue.m_BackIndex ) ?
_queue.m_BackIndex - _queue.m_FrontIndex :
_queue.m_BackIndex + _queue.m_Size - _queue.m_FrontIndex;
}
boolIntegerQueueIsEmpty ( constIntegerQueue & _queue )
{
returnIntegerQueueSize( _queue ) == 0;
}
boolIntegerQueueIsFull ( constIntegerQueue & _queue )
{
returnIntegerQueueSize( _queue ) == ( _queue.m_Size - 1 );
}
intIntegerQueueNextIndex ( constIntegerQueue & _queue, int_index )
{
intindex = _index + 1;
if( index == _queue.m_Size )
index = 0;
returnindex;
}
voidIntegerQueuePush ( IntegerQueue & _queue, int_value )
{
assert( ! IntegerQueueIsFull( _queue ) );
_queue.m_pData[ _queue.m_BackIndex ] = _value;
_queue.m_BackIndex = IntegerQueueNextIndex( _queue, _queue.m_BackIndex );
}
voidIntegerQueuePop ( IntegerQueue & _queue )
{
assert( ! IntegerQueueIsEmpty( _queue ) );
_queue.m_FrontIndex = IntegerQueueNextIndex( _queue, _queue.m_FrontIndex );
}
intIntegerQueueFront ( constIntegerQueue & _queue )
{
assert( ! IntegerQueueIsEmpty( _queue ) );
return_queue.m_pData[ _queue.m_FrontIndex ];
}
Выводы
В данной лекции было введено понятие абстрактного типа данных (АТД), показана его роль при неформальном анализе алгоритмов. АТД определяют набор требуемых абстрактных операций, которые должна обеспечить конкретная реализация. Может существовать несколько реализаций АТД, при этом операции будут обладать различной производительностью. Модульный стиль разбиения программ позволяет делать разные реализации АТД взаимозаменяемыми и выбирать между ними в зависимости от потребностей конкретной задачи. Были детально рассмотрены простейшие АТД - списки, стеки, очереди, а также способы их реализации и применения.
Дата добавления: 2016-01-29; просмотров: 3128;
