в) Короткозамкнутые двигатели. 2 страница
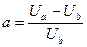 ;
; 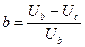 .
.
Далее рассчитываем:
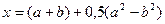 ;
; 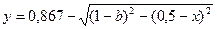 .
.
После этого получим:
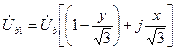 ;
;
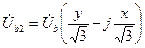
и отсюда модули симметричных составляющих:
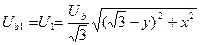 ;
;
 .
.
При симметричных обмотках статора и ротора мы можем считать, что обе системы напряжений U1 и U2, действуют независимо одна от другой При U1 > U2 ротор будет вращаться в сторону вращения поля, соответствующего напряжениям прямой последовательности U1. Будем это поле называть прямо вращающимся или прямым.
По отношению к напряжениям U1 машина будет работать в режиме двигателя со скольжением 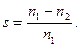 По круговой диаграмме или расчетным путем, как указывалось ранее, мы можем найти токи статора и ротора I1, и
По круговой диаграмме или расчетным путем, как указывалось ранее, мы можем найти токи статора и ротора I1, и 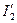 вращающий момент М при любом скольжении s. Токи I1, вызванные напряжениями U1, являются токами прямой последовательности.
вращающий момент М при любом скольжении s. Токи I1, вызванные напряжениями U1, являются токами прямой последовательности.
Поле, соответствующее напряжениям обратной последовательности U2 будет вращаться против вращения ротора. Будем его называть обратно вращающимся или обратным. По отношению к напряжениям U2 машина будет работать в режиме тормоза со скольжением
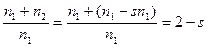 .
.
Токи статора, вызванные напряжениями U2, являются токами обратной последовательности. Обозначим их через I12. Токи 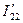 , наведенные в обмотке ротора обратным полем, будут иметь частоту (2 — s)f1 При малом s эта частота почти в 2 раза больше частоты тока статора.
, наведенные в обмотке ротора обратным полем, будут иметь частоту (2 — s)f1 При малом s эта частота почти в 2 раза больше частоты тока статора.
3-21.3. Работа при несимметричных напряжениях
Токи I12 и 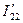 можно определить по упрощенной схеме замещения, представленной на рис 3-73.
можно определить по упрощенной схеме замещения, представленной на рис 3-73.
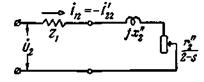
Рис. 3-73. Приближенная схема для определения тока обратной последовательности.
Здесь мы пренебрегаем током синхронизма и принимаем с1 = 1, что допустимо при U2 << U1. Сопротивления 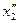 и
и 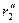 являются сопротивлениями роторной обмотки, приведенными к статорной обмотке и рассчитанными с учетом вытеснения тока. Вытеснение тока здесь необходимо учитывать, так как частота тока ротора почти равна 2f1. Для двигателей с глубокими пазами и с двойной клеткой на роторе
являются сопротивлениями роторной обмотки, приведенными к статорной обмотке и рассчитанными с учетом вытеснения тока. Вытеснение тока здесь необходимо учитывать, так как частота тока ротора почти равна 2f1. Для двигателей с глубокими пазами и с двойной клеткой на роторе 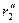 может быть больше
может быть больше 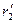 (рассчитанного без учёта вытеснения тока) в 5-6 раз. Для фазного ротора, имеющего стержневую двухслойную обмотку при высоте стержней 1 см и больше, также получается заметное увеличение
(рассчитанного без учёта вытеснения тока) в 5-6 раз. Для фазного ротора, имеющего стержневую двухслойную обмотку при высоте стержней 1 см и больше, также получается заметное увеличение 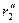 по сравнению с
по сравнению с 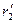 .
.
Сопротивление схемы рис. 3-73 приблизительно равно сопротивлению короткого замыкания zк; следовательно, приближенно можем написать
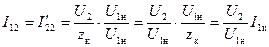 , (3-188)
, (3-188)
где  — ток короткого замыкания при напряжении U1н. Ранее указывалось, что для нормальных двигателей
— ток короткого замыкания при напряжении U1н. Ранее указывалось, что для нормальных двигателей 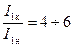 , поэтому, учитывая (3-188), получим:
, поэтому, учитывая (3-188), получим:
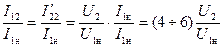 . (3-189)
. (3-189)
Из (3-189) следует, что ток обратной последовательности может иметь большое значение: например, даже при 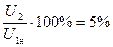 токи I12 и
токи I12 и 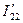 будут составлять 20
будут составлять 20 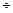 30% номинального тока I1н.
30% номинального тока I1н.
Тормозящий момент М2, соответствующий работе тормозом при U2, в обычных случаях несимметрии напряжений мал и им можно пренебречь Действительно, момент от обратного поля 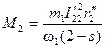 ; момент от прямого поля
; момент от прямого поля 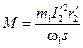 , следовательно
, следовательно
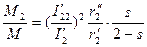 .
.
Мы видим, что при 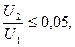 когда
когда 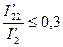 , и при обычных скольжениях s = 0,02
, и при обычных скольжениях s = 0,02 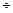 0,05, соответствующих номинальной нагрузке на валу, момент М2 не превышает в худшем случае 0,02 М.
0,05, соответствующих номинальной нагрузке на валу, момент М2 не превышает в худшем случае 0,02 М.
Таким образом, ухудшение условий работы двигателя при несимметрии напряжений на его зажимах получается в основном из-за увеличения электрических потерь в его обмотках. Потери в роторной обмотке увеличиваются на  , (так как частоты токов
, (так как частоты токов 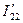 и
и 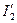 сильно отличаются одна от другой, и поэтому мы можем считать, что общие потери в роторной обмотке равны
сильно отличаются одна от другой, и поэтому мы можем считать, что общие потери в роторной обмотке равны 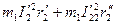 . Общие потери в статорной обмотке увеличиваются на
. Общие потери в статорной обмотке увеличиваются на  (так как из общих уравнений метода симметричных составляющих следует, что электрические потери в трехфазной обмотке при наличии в ней токов прямой и обратной последовательностей равны
(так как из общих уравнений метода симметричных составляющих следует, что электрические потери в трехфазной обмотке при наличии в ней токов прямой и обратной последовательностей равны 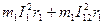 ).
).
Приходится также считаться с тем, что в наихудшем случае в одной из фаз токи прямой и обратной последовательностей складывается арифметически (рис. 3-74). Нагревание ее в этом случае может быть чрезмерным.
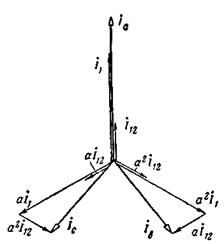
Рис. 3-74. Определение токов фаз по их симметричным составляющим.
Отметим здесь, что асинхронный двигатель при его работе вхолостую или с нагрузкой создает выравнивающее действие на напряжения сети, к которой он подключен, т. е. уменьшает их несимметрию. Объясняется это тем, что распределение токов по фазам сети и обмотки статора будет соответствовать напряжениям фаз: больший ток будет поступать в ту фазу обмотки статора, к которой приложено большее напряжение. Выравнивающее действие трехфазного асинхронного двигателя на напряжения сети будет тем больше, чем меньше zк двигателя.
3-21.4. Работа при несинусоидальном напряжении
Если кривая напряжения сети, к которой подключен двигатель, имеет высшие гармоники, то действие каждой гармоники с частотой fn = nf1 можно рассматривать отдельно, так же как и действие основной (первой) гармоники При этом следует иметь в виду, что все индуктивные сопротивления и частота вращения поля при более высокой частоте (n > l) будут в n раз больше, чем при основной частоте напряжения. Но число полюсов вращающегося поля, соответствующего n-й гармонике напряжения, будет равно числу полюсов основного поля (здесь рассматриваются только основные пространственные гармоники н.с. и, следовательно, полей статора).
Скольжение ротора относительно поля, соответствующего n-й гармонике напряжения,
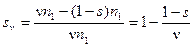 ,
,
где s — скольжение ротора относительно основного поля. При номинальном режиме работы
двигателя скольжение sn 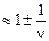 . Оно мало отличается от 1 (при n > 5), т. е. практически можно принять, что двигатель по отношению к системе напряжений с частотой nf1, находится в покое (sn
. Оно мало отличается от 1 (при n > 5), т. е. практически можно принять, что двигатель по отношению к системе напряжений с частотой nf1, находится в покое (sn 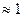 ).
).
Тогда добавочный ток, созданный этой системой напряжений,
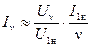 ,
,
где Un — v-я гармоника напряжения; I1к 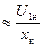 — ток короткого замыкания (xк
— ток короткого замыкания (xк  .
.
Ток статора In и соответствующий ему ток ротора 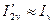 вызовут в обмотках машины электрические потери. Созданный ими вращающий момент практически ничтожен. Он приближенно равен:
вызовут в обмотках машины электрические потери. Созданный ими вращающий момент практически ничтожен. Он приближенно равен:
 ,
,
где Мнач — начальный вращающий момент при U1н без учета насыщения от полей рассеяния и вытеснения тока в проводниках ротора. При учете вытеснения тока в проводниках ротора Mn будет больше главным образом из-за увеличения активного сопротивления обмотки ротора Но и в этом случае его значение очень мало.
Добавочные электрические потери от токов Iν и 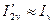 в обмотках машины равны:
в обмотках машины равны:
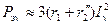 ,
,
где 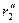 — активное сопротивление обмотки ротора, приведенное к обмотке статора и учитывающее вытеснение тока при f2
— активное сопротивление обмотки ротора, приведенное к обмотке статора и учитывающее вытеснение тока при f2 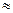 nf1. Общие добавочные электрические потери в обмотках машины получим, просуммировав потери Pэn от всех гармоник тока.
nf1. Общие добавочные электрические потери в обмотках машины получим, просуммировав потери Pэn от всех гармоник тока.
Если кривая напряжения сети, к которой подключен двигатель, имеет высшие гармоники, то действие каждой гармоники с частотой fn = nf1 можно рассматривать отдельно, так же как и действие основной (первой) гармоники При этом следует иметь в виду, что все индуктивные сопротивления и частота вращения поля при более высокой частоте (n > l) будут в n раз больше, чем при основной частоте напряжения. Но число полюсов вращающегося поля, соответствующего n-й гармонике напряжения, будет равно числу полюсов основного поля (здесь рассматриваются только основные пространственные гармоники н.с. и, следовательно, полей статора).
Скольжение ротора относительно поля, соответствующего n-й гармонике напряжения,
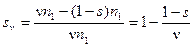 ,
,
где s — скольжение ротора относительно основного поля. При номинальном режиме работы
двигателя скольжение sn 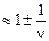 . Оно мало отличается от 1 (при n > 5), т. е. практически можно принять, что двигатель по отношению к системе напряжений с частотой nf1, находится в покое (sn
. Оно мало отличается от 1 (при n > 5), т. е. практически можно принять, что двигатель по отношению к системе напряжений с частотой nf1, находится в покое (sn 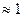 ).
).
Тогда добавочный ток, созданный этой системой напряжений,
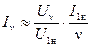 ,
,
где Un — v-я гармоника напряжения; I1к 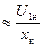 — ток короткого замыкания (xк
— ток короткого замыкания (xк  .
.
Ток статора In и соответствующий ему ток ротора 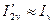 вызовут в обмотках машины электрические потери. Созданный ими вращающий момент практически ничтожен. Он приближенно равен:
вызовут в обмотках машины электрические потери. Созданный ими вращающий момент практически ничтожен. Он приближенно равен:
 ,
,
где Мнач — начальный вращающий момент при U1н без учета насыщения от полей рассеяния и вытеснения тока в проводниках ротора. При учете вытеснения тока в проводниках ротора Mn будет больше главным образом из-за увеличения активного сопротивления обмотки ротора Но и в этом случае его значение очень мало.
Добавочные электрические потери от токов Iν и 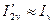 в обмотках машины равны:
в обмотках машины равны:
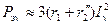 ,
,
где 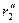 — активное сопротивление обмотки ротора, приведенное к обмотке статора и учитывающее вытеснение тока при f2
— активное сопротивление обмотки ротора, приведенное к обмотке статора и учитывающее вытеснение тока при f2 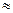 nf1. Общие добавочные электрические потери в обмотках машины получим, просуммировав потери Pэn от всех гармоник тока.
nf1. Общие добавочные электрические потери в обмотках машины получим, просуммировав потери Pэn от всех гармоник тока.
3-21.5. Работа при неравных сопротивлениях фаз ротора
При неравных сопротивлениях фаз ротора токи их также не равны между собой. Они образуют несимметричную систему, которую мы можем заменить двумя симметричными системами, имеющими взаимно обратное чередование фаз. Возможность такой замены подтверждается следующими рассуждениями.
Каждая фаза ротора создает пульсирующую н.с. Ее мы можем заменить двумя н.с., вращающимися в разные стороны с одинаковыми частотами (§ 3-4,а). Таким образом, при числе фаз ротора m2 мы получим m2 н.с., вращающихся в одну сторону, и m2 н.с., вращающихся в другую сторону. Суммируя отдельно те и другие, получим только две н.с., вращающиеся в разные стороны Такие же н.с. создадут токи прямой и обратной последовательностей, которыми мы заменили действительные токи фаз ротора.
В машине возникнут два вращающихся поля. Одно из них (основное) будет создаваться токами прямой последовательности ротора Iр1 и соответствующими им токами статора Iс1. Оно будет наводить в обмотке статора э.д.с. Ec1, почти равную при малых скольжениях приложенному к статору напряжению U1. Второе поле будет вызвано токами обратной последовательности ротора Iр2 и токами Iс2, наведенными им в обмотке статора.
При скольжении s ротора относительно первого (основного) поля его н.с. от токов прямой последовательности вращается относительно ротора в сторону его вращения с частотой sn1 соответственно частоте f2 = sf1. Токи ротора обратной последовательности, имеющие ту же частоту f2, создадут н.с., вращающуюся относительно ротора с той же частотой sn1, но в сторону, противоположную его вращению. Эти токи мы должны рассматривать как первичные. Соответствующее им поле вращается относительно статора с частотой
 . (3-190)
. (3-190)
Оно будет наводить в обмотке статора токи, имеющие частоту
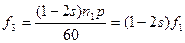 . (3-191)
. (3-191)
Эти токи будут замыкаться через сеть и налагаться на токи основной частоты f1.
При малом значении s частота f3 близка к частоте f1; например, при s = 0,01 и при f1 = 50 Гц получим f3= (1 - 2 0,01) 50 = 49 Гц.
При наложении токов частот f1 и f3 (так же как при наложении колебаний с мало различающимися частотами) получается резко выраженная картина биений, что приводит к колебаниям стрелки амперметра в цепи статора с частотой (f1 - f3). Такие колебания стрелки амперметра обычно указывают на неисправности цепи ротора. Если измерить их частоту, то можно, зная f1, найти f3 и, следовательно, определить по (3-191) скольжение двигателя s. При скольжении s, близком к 0,5, колебания стрелки амперметра в цепи статора также будут заметны, но частота их будет равна f3.
Рассмотрим вращающие моменты, которые создаются в машине при неравных сопротивлениях фаз ротора. Вначале рассмотрим момент, созданный обратным полем ротора. Для этого обратимся к рис. 3-75, где представлены статор и ротор машины, причем здесь условно (пунктиром и стрелками) показано поле северной полярности, вращающееся против вращения ротора с частотой sn1.

Рис. 3-75. К определению направления момента М2 от обратного поля.
По правилу правой руки найдем направление тока, наведенного этим полем в обмотке статора, а по правилу левой руки — направление электромагнитного момента М2, действующего на статор. На ротор действует такой же момент М2, но в обратную сторону.
На рис. 3-75, а и б видим, что при s > 0,5 момент M2 действует на ротор в направлении его вращения, а при s < 0.5 — в обратном направлении. При s = 0,5 обратное поле ротора относительно статора неподвижно и никаких токов в статорной обмотке не создает; при этом M2 = 0.
Момент М1, получающийся от взаимодействия основного поля и токов ротора прямой последовательности Iр1 при малом активном сопротивлении его цепей может быть, как показывает анализ, также отрицательным при s 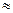 0,5 из-за большого сдвига по фазе токов относительно э.д.с.
0,5 из-за большого сдвига по фазе токов относительно э.д.с.
Исследование работы трехфазного асинхронного двигателя при несимметрии фаз ротора будем проводить применительно к двигателю с контактными кольцами, имеющему в роторе трехфазную обмотку.
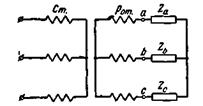
Рис. 3-76. Схема двигателя с неравными сопротивлениями фаз ротора.
Обратимся к рис. 3-76. Для роторных целей можем написать следующие уравнения напряжений:
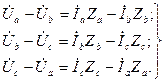 (1-192)
(1-192)
Заменим напряжения и токи их симметричными составляющими, учтя при этом что составляющие нулевой последовательности отсутствуют. Обозначим составляющие прямой и обратной последовательностей в, фазе ротора а соответственно через 
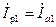 и
и 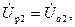
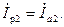 При этом будем считать, что все величины ротора приведены к обмотке статора.
При этом будем считать, что все величины ротора приведены к обмотке статора.
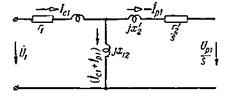
Рис. 3-77. Схема замещения. соответствующая токам прямой последовательности ротора.
Решая полученную систему уравнений в отношении 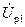 и
и 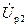 , получим:
, получим:
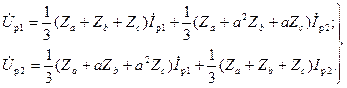 (3-193)
(3-193)
Теперь можем написать уравнения напряжений статора и ротора прямой последовательности:
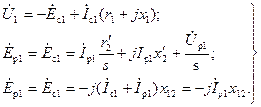 (3-194)
(3-194)
Уравнениям (3-194) соответствует схема замещения для напряжений и токов прямой последовательности, представленная на рис. 3-77.
Уравнения напряжений ротора и статора обратной последовательности имеют следующий вид:
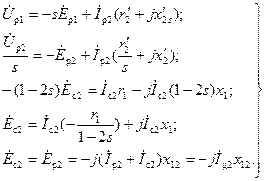 (3-195)
(3-195)
Мы считаем, что напряжение 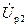 приложено к обмотке ротора, вращающегося со скольжением s относительно основного поля. Рассматривая работу машины, получающей питание со стороны ротора (к обмотке ротора приложено напряжение Uр2 переменной частоты sf1), видим, что при s > 0,5 машина работает двигателем, так как ротор при этом вращается медленнее, чем обратное поле, а при s < 0,5 машина работает генератором, так как в этом случае ротор вращается быстрее, чем обратное поле.
приложено к обмотке ротора, вращающегося со скольжением s относительно основного поля. Рассматривая работу машины, получающей питание со стороны ротора (к обмотке ротора приложено напряжение Uр2 переменной частоты sf1), видим, что при s > 0,5 машина работает двигателем, так как ротор при этом вращается медленнее, чем обратное поле, а при s < 0,5 машина работает генератором, так как в этом случае ротор вращается быстрее, чем обратное поле.
В последних трех уравнениях (3-195) Ec2 — э. д. с статора, которая наводится в его обмотке обратным полем, т. е. полем токов Iр2 и Iс2, при s = l. При s 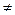 1 э. д. с. Eс2(1 - 2s) имеет частоту (1 - 2s)f1 так же как и вызываемый ею ток Iс2.
1 э. д. с. Eс2(1 - 2s) имеет частоту (1 - 2s)f1 так же как и вызываемый ею ток Iс2.
Уравнениям (3-195) соответствует схема замещения для напряжений и токов обратной последовательности, представленная на рис. 3-78.
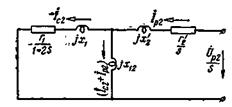
Рис. 3-78. Схема замещения, соответствующая токам обратной последовательности ротора.
При помощи схем замещения и уравнений (3-193) можно составить формулы для определения 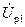 ,
, 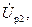
 ,
, 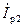
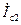 и, следовательно, М1 и M2. Однако они получаются довольно громоздкими и требуют кропотливых расчетов.
и, следовательно, М1 и M2. Однако они получаются довольно громоздкими и требуют кропотливых расчетов.
Рассмотрим как имеющий большее практическое значение частный случай, когда Za = ∞, Zb = 0 и Zc=0, т. е. когда фаза а разомкнута, а фазы b и с замкнуты накоротко (рис. 3-79).
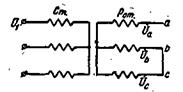
Рис. 3-79. Схема двигателя при одноосном включении обмотки ротора.
Для этого случая имеем:
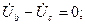
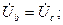
 ;
;
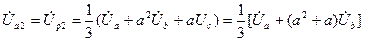 ;
;
следовательно,
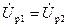 ; (3-196)
; (3-196)
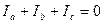 ;
; 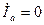 ;
;  ;
;
 ;
;
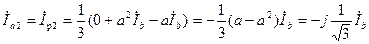 ;
;
следовательно,
 . (3-197)
. (3-197)
Так как 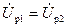 и
и  , то схемы, представленные на рис. 3-77 и 3-78, могут быть объединены; тогда получится схема, представленная на рис. 3-80.
, то схемы, представленные на рис. 3-77 и 3-78, могут быть объединены; тогда получится схема, представленная на рис. 3-80.
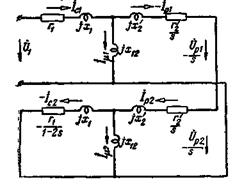
Рис. 3-80. Схема замещения двигателя при одноосном включении обмотки ротора.
Этой объединенной схеме соответствует схема замещения агрегата, состоящего из двух идентичных машин, соединенных механически и электрически, как показано на рис. 3-81.
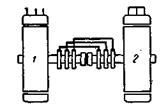
Рис. 3-81. Агрегат из двух асинхронных машин, соответствующий схеме рис. 3 80.
Здесь вторая машина соединена с первой машиной таким образом, чтобы момент, создаваемый ею при 0,5<s<l, был направлен в ту же сторону, что и момент первой машины. Приведённая схема будет приближенной для случая s = 1, так как при этом f3 = f1(1 - 2s) = -fi и обмотку статора только приближенно можно рассматривать короткозамкнутой по отношению к э.д.с. частоты f3 = -f1.
Расчет токов и моментов может быть произведен при помощи схемы на рис. 3-80. Однако практически достаточно точные результаты получаются при расчетах по упрощенной схеме, представленной на рис. 3-82.
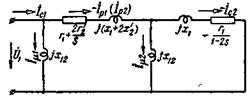
Рис. 3-82. Упрощенная схема замещения двигателя при одноосном включении обмотки ротора.
Расчетные формулы будем составлять при помощи этой схемы (потери в стали статора, которые не учитывались в представленных схемах замещения, могут быть учтены при расчете электромагнитных моментов).
Сначала по схеме на рис. 3-82 найдем полное сопротивление Z1 определяющее ток  ;
;
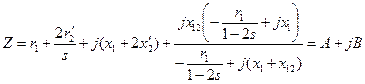 , (3-198)
, (3-198)
где
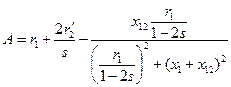 (3-199)
(3-199)
[последний член правой части при s = 0,5 paвен нулю, в чем можно убедиться, умножив числитель и знаменатель на (1 - 2s)];
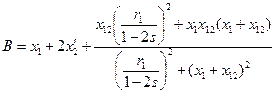 (3-200)
(3-200)
[последний член правой части при s = 0,5 равен х12, что получим, если умножим числитель и знаменатель на (1 - 2s)2]. Значения А и В при s = 0,5 можно найти непосредственно из схемы замещения на рис. 3-82. Они, очевидно, будут такими же, как и найденные по (3-199) и (3-200), с учетом того, что отмечено в квадратных скобках.
Теперь можем определить модуль тока ротора:
 . (3-201)
. (3-201)
Действительный ток ротора в его замкнутых фазах равен 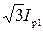 .
.
Вращающий момент от взаимодействия основного поля и токов ротора Ip1 определяется по следующей формуле, синхронных Bт:
М1 = m1 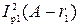 . (3-202)
. (3-202)
Для определения модуля тока Iс2 согласно схеме на рис. 3-82 можем написать следующее уравнение:
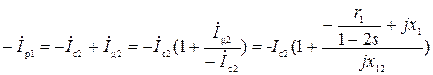 ;
;
отсюда
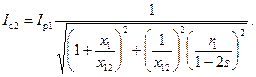 (3-203)
(3-203)
Вращающий момент от взаимодействия обратного поля и токов статора Iс2 определяется по формуле, синхронных ваттах,
Дата добавления: 2016-01-29; просмотров: 1107;
