Расчет параметров сетевого графика
| Количество непосредственно предшествующих работ | Шифр работы | Продолжительность работы,
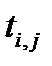
| Сроки работы | Резервы работ | |||||
| Ранние | Поздние | ||||||||
| i | j | раннее начало, 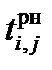
| раннее окончание, 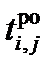
| позднее начало, 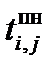
| позднее окончание,
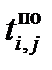
| полные, Rп | свобод- ные, Rс | ||
| – | |||||||||
Окончание табл. 7
| Количество непосредственно предшествующих работ | Шифр работы | Продолжительность работы,
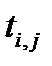
| Сроки работы | Резервы работ | |||||
| Ранние | Поздние | ||||||||
| i | j | раннее начало, 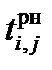
| раннее окончание, 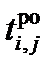
| позднее начало, 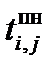
| позднее окончание,
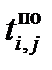
| полные, Rп | свобод- ные, Rс | ||
| – |
В гр. 5, 6 записывается расчет ранних параметров работ – раннее начало и раннее окончание. Расчет ведется от исходного события до завершающего. Для простых событий (в которые входит только одна работа) раннее начало работы равно раннему окончанию предшествующей работы. Раннее окончание работы равно сумме ее раннего начала, плюс продолжительность данной работы, т.е. данные гр. 5 плюс данные гр. 4, результат заносится в гр. 6.
Например: раннее начало исходной работы (1–2) равно 0 (гр. 5); раннее окончание работы (1–2) равно 2 (0 + 2). Ранний срок начала работ, начинающихся одним и тем же событием, всегда одинаков. Поэтому ранний срок начала работ (2–3) и (2–5) принимаем равным 2 (гр. 5).
Раннее окончание работы (1–2) равно 2 (0 + 2); результаты заносятся в гр. 6. Работе
(2–3) предшествует работа (1–2), для которой раннее окончание предшествующей работы равно 2 (гр. 6). Так как раннее окончание предшествующей работы равно раннему началу последующей работы, то число 2 записывается в гр. 5 как раннее начало рассматриваемой работы (2–3). Прибавив к 2 продолжительность работы 2, результат записывается в гр. 6 (число 4). Раннее начало работы (2–5) также равно 2, так как ей предшествует событие 2.
В гр. 5 против кода этих работ записывается результат 2, а в гр. 6 заносится соответственно результат 4 (2 + 2). Работам (3–4) и (3–7) также предшествует только одна работа (2–3), поэтому в гр. 5 заносится результат 4, в гр. 6 результаты 6 (4 + 2) и 4 (2 + 2). Следующие расчеты проводятся аналогично вышеописанным расчетам.
При рассмотрении сложного события (когда ему предшествуют две и более работ), раннее начало последующей работы будет соответствовать максимальному значению ранних окончаний предшествующих работ. В данном примере работы (7–8), (12–14), (15–16),
(17–24), (20–21), (22–23), (24–25), (27–28) и (31–32) имеют по 2 предшествующие работы
(см. гр. 1).
Например, работе (7–8) предшествуют работы (3–7) и (6–7) с начальными событиями
3 и 6. Так как ранние характеристики работ (в том числе работ (3–7) и (6–7)) рассчитаны, то остается сравнить их величины. Раннее окончание работы (3–7) равно 4, а раннее окончание работы (6–7) равно 6. В гр. 5 для работы (7–8) заносится большее значение (6), затем определяется раннее окончание работы, равное 7 (6 + 1 = 7). Аналогично выполняем расчеты для всех остальных работ, имеющих две и более предшествующих.
В гр. 7, 8 записываются расчеты поздних параметров работ: позднее начало и позднее окончание. Расчет ведется в обратном порядке, т. е. от завершающих работ до исходных работ, снизу вверх. Для простого события (из которого выходит только одна работа) позднее окончание предшествующей работы равно позднему началу рассматриваемой работы. Позднее начало данной работы равно разности между ее поздним окончанием и продолжительностью, т. е.
ti.jпн = ti.jпо – ti j. (7)
Для сложного события (из которого выходит несколько работ) позднее окончание предшествующих работ равно меньшему значению из поздних начал рассматриваемых работ. При сравнении ранних сроков окончания всех работ берется максимальное значение ранних сроков окончания работ (Ткр=18).
Например, для работ, заканчивающихся событием № 32, поздний срок окончания работ равен Ткр. В гр. 8 для работы (31–32) заносится значение позднего срока окончания работ (18). В гр. 7 для работы (31–32) заносится результат разности значений гр. 8 и гр. 4
(18 – 2 = 16). В гр. 8 работы (30–31) заносится значение из гр. 7 работы (31–32), равное 16 (так как они имеют общее событие 31). Дальнейший расчет ведется снизу вверх аналогично выше описанному расчету.
При расчетах несложных и сложных событий нужно обратить внимание на некоторые отличия: несложные события рассчитываются аналогично описанным выше; при расчете сложных событий (имеющих две и более последующих работ) необходимо выбирать минимальное значение из нескольких вариантов поздних сроков начал этих работ, которые указаны в гр. 7. Контролем правильности расчета является нулевое значение одного из поздних сроков начала исходных работ.
В гр. 9 (полный резерв времени) заносится результат разности значений гр. 7 и гр. 5 или гр. 8 и гр. 6:
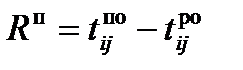 или
или 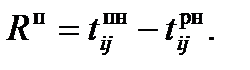 (8)
(8)
Наличие полного резерва времени у работы означает, что эту работу можно начать позже или увеличить продолжительность её выполнения на величину полного резерва.
Например, полный резерв времени работы (1–2) рассчитывается следующим образом: 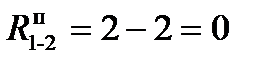 или
или 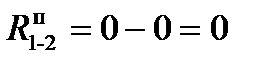 ; полный резерв работы (2–3) равен
; полный резерв работы (2–3) равен 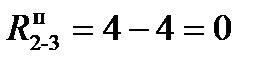 или
или 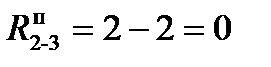 и т.д.
и т.д.
В гр. 10 (свободный резерв времени) заносится результат разности раннего начала последующей работы (гр. 5) и раннего окончания данной работы (гр. 6):
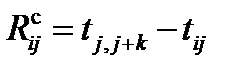 . (9)
. (9)
Наличие свободного резерва времени у работы означает, что данную работу можно начать позже или увеличить ее продолжительность без изменения ранних сроков начал следующих работ.
При расчете гр. 10 нужно обратить внимание на то, что те работы, которые не имеют полного резерва времени, не могут иметь и свободного резерва времени, следовательно,
в гр. 10 для этих работ заносится результат 0.
Например, первой работой, имеющей свободный резерв времени, является работа (3–7). Он рассчитывается следующим образом: в гр. 2 находится событие, равное конечному событию работы (3–7) (в данном примере это работа (7–8)); в гр. 10 для работы (3–7) заносится результат разности гр. 5 работы (7–8) и гр. 6 работы (3–7): (6 – 4 = 2). Дальнейшие расчеты проводятся аналогично вышеописанным расчетам.
Критический путь при табличном методе расчета лежит на тех работах, полный и свободный резервы времени которых равны 0 (критические работы). К таким работам относятся все работы, имеющие результат 0 в гр. 9 и гр. 10 (выделены жирным шрифтом). Продолжительность критического пути равна сумме продолжительностей входящих в него критических работ. В нашем примере Tкр = 18 (гр. 5). На графике критический путь должен представлять собой непрерывную последовательность работ от начального события до конечного события.
Анализируя таблицу, мы получаем сведения: о длине критического пути; ранних
и поздних началах и окончаниях каждой из работ; полных и свободных резервах времени.
Корректировка сетевых графиков производится как на этапе их составления, так и использования. Она состоит в оптимизации строительных работ по времени и по ресурсам
(в частности по движению рабочей силы). Если, например, сетевой график не обеспечивает выполнения работ в необходимые сроки (нормативные или установленные контрактом) производится его корректировка по времени, т. е. сокращается продолжительность критического пути. Обычно это делается:
– за счет резервов времени некритических работ и соответствующего перераспределения ресурсов;
– за счет привлечения дополнительных ресурсов;
– за счет изменения организационно-технологической последовательности и взаимосвязи работ.
Для расчета сетевого графика на ПЭВМ разработан пакет программ, который, кроме параметров времени работ позволяет определить также продолжительность критического пути (общую продолжительность выполнения комплекса работ).
Данная программа не учитывает принципы поточного (непрерывного) выполнения процессов на участках, то есть предполагается, что каждая работа начинается сразу, как только открывается фронт работ для нее (позволяет технологическая возможность ее выполнения). Считается целесообразным производить расчет масштабной сетевой модели следующим образом.
1. Ввод исходных данных.
Программа расчета сетевых моделей (далее – СМ) находится на локальном диске С – папка «FOX».
Программа включает в себя пакет файлов, необходимых для расчета. В пакет входят файлы для ввода исходных данных, для расчета параметров СМ, для корректировки СМ и т.д.
Для ввода исходных данных нужно открыть приложение START в папке «FOX».
В открывшемся пользователю файле появится диалоговое окно (рис. 22).
| C:\ WINNT \ Sistem 32\ cmd.exe | ||
Программа расчета сетевого графика
|
Рис. 22. Стартовое диалоговое окно программы «FOX»
Курсор устанавливается на строку ВВОД ИСХОДНЫХ ДАННЫХ , далее нажать клавишу ENTER . На дисплее появляется диалоговое окно (рис. 23). Имя для таблицы исходных данных: вводится от трех до восьми символов на английском языке.
По окончании ввода нажмите ENTER |
Рис. 23. Диалоговое окно «Ввод исходных данных»
В открывшемся пользователю окне содержится информация о содержании вводимой исходной информации, необходимой для расчета всех параметров СГ (рис. 24).
НАЧИНАЕТСЯ ВВОД ИСХОДНЫХ ДАННЫХ
|
Рис. 24. Диалоговое окно «Ввод исходных данных»
После нажатия клавиши ENTER появляется таблица для ввода исходных данных
(рис. 25).
| (имя файла) | ||
| i j Tij | ||
| Для выхода нажмите ENTER |
Рис. 25. Вид таблицы ввода исходных данных
Исходная информация вводится при помощи клавиши ENTER (рис. 26).
| (имя файла) |
| I 1 Enter J 2 Enter Ti,j 2 Enter |
| Для выхода нажмите ENTER |
Рис. 26. Ввод информации
Если по ошибке введена и сразу замечена неточная вводимая информация, то курсором ↑ возвращайтесь на строку, где сделана ошибка, и поверх введенной информации введите нужную информацию, по окончании ввода исправления нажать ENTER.
2. После ввода всей таблицы исходных данных нажать Esc, на мониторе появляется диалоговое окно (рис. 27).
Программа расчета сетевого графика
|
Рис. 27. Диалоговое окно «Программа расчета сетевого графика»
Выбираем строку «Расчет параметров СГ» и нажатием команды ENTER на экране появится рассчитанная СЕТЕВАЯ МОДЕЛЬ с указанием работ критического пути. Просмотр результатов расчета можно увидеть, выбрав строку «Просмотр результатов». При этом программа запросит у вас ввести имя файла.
Если СМ закодирована правильно и внимательно введена таблица исходных данных, то рассчитанная СМ будет содержать значок «*» напротив определенных строчек в последнем столбце. Работа, содержащая значок «*», является критической (табл. 8).
Критический путь должен пройти от исходного до завершающего события непрерывно, критический путь имеет максимальную продолжительность.
Таблица 8
Расчёт параметров сетевого графика
| Код работы | Продолжительность работы, tij | Раннее начало работы, TRN | Раннее окончание работы, TRO | Позднее начало работы, TPN | Позднее окончание работы, TPO | Полный резерв работы, RP | Свободный резерв работы, RC | Работы критического пути, Rкр | |
| Код начального события, i | Код конечного события, j | ||||||||
| * | |||||||||
| * | |||||||||
| * | |||||||||
| * | |||||||||
| * | |||||||||
| * | |||||||||
| * | |||||||||
| * | |||||||||
| * |
Если столбцы таблицы с рассчитанными параметрами СМ содержат знак «минус», то:
1) СМ закодирована неверно,
2) пропущены либо работа, либо зависимость при вводе исходных данных.
Для исправления данных выбираем в программе строку «корректировка данных» и нажимаем ENTER.
Появится диалоговое окно с вопросами:
Добавить работы? и Изменить данные?
Выбираем нужную команду и производим корректировку данных.
Для вывода окончательного решения расчета СМ используется программа EXСEL.
В папке «FOX» находим файл TGASU 1, который является файлом результата расчета СМ, открываем его с помощью программы EXСEL и выводим информацию на бумагу.
- ПРОЕКТИРОВАНИЕ ГРАФИКА ПОСТУПЛЕНИЯ НА ОБЪЕКТ
Дата добавления: 2016-01-29; просмотров: 1463;
