Современные представления о строении атома. Для квантовомеханического описания атома необходимо решить уравнение Шредингера

Для квантовомеханического описания атома необходимо решить уравнение Шредингера. Эта достаточно непростая задача успешно решена для атома водорода и водородоподобных ионов.

Согласно квантовой механике, энергия электрона в атоме, его орбитальный момент импульса, проекция момента импульса на выделенное направление в пространстве и проекция собственного момента импульса электрона (спина) на это направление дискретны или квантованы.

Состояние электрона в атоме описывается набором четырех квантовых чисел: n, l, m и s.

n называется главным квантовым числом и характеризует энергию электрона в атоме:

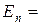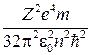− . (2.9.4)

Орбитальное число l характеризует момент импульса электрона в атоме:

L = 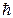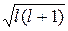. (2.9.5)

Магнитное число m определяет проекцию момента импульса на выделенное направление в пространстве (например, на направление магнитного поля):

L_z = 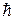m. (2.9.6)

Электрон и ряд других элементарных частиц обладают собственным механическим моментом импульса (спином), не связанным с их движением в пространстве. Спиновое число s характеризует проекцию момента импульса электрона на выделенное направление в пространстве.

При переходе с одного энергетического уровня (E_m) на другой (E_n) атом испускает или поглощает квант энергии электромагнитного поля (фотон)

hn=E_m – E_n. (2.9.7)

Квантовомеханическое описание многоэлектронных атомов является еще более трудной задачей, нежели описание атома водорода. В многоэлектронных системах проявляются особые свойства, не имеющие аналогов в классической физике. В классической механике частицы, обладающие одинаковыми физическими параметрами (масса, электрический заряд, размер и др.), принципиально можно различить по их положению в пространстве и импульсам. Такие частицы называются тождественными. Волновые свойства микрообъектов приводят к тому, что тождественные микрочастицы принципиально неразличимы. Для микрочастиц неприменимо понятие траектории, состояние микрочастицы описывается волновой функцией, квадрат модуля которой позволяет вычислять лишь вероятность нахождения микрочастицы в окрестности той или иной точки пространства. В области перекрытия волновых функций вопрос об индивидуальности той или иной частицы лишен смысла. Принцип неразличимости тождественных частиц является одним из фундаментальных принципов квантовой механики.

Принцип неразличимости тождественных частиц приводит к особым чертам в поведении электронов в многоэлектронных атомах. Эти особенности сконцентрированы в принципе, сформулированном В. Паули (1925): в атоме не могут находиться два электрона, обладающих одинаковым набором квантовых чисел. Согласно принципу Паули, у любых двух электронов в атоме не может быть четырех одинаковых квантовых чисел (главное n, орбитальное l, магнитное m и спиновое s), значения по крайней мере одного квантового числа должны различаться.

Принцип Паули лежит в основе заполнения электронных состояний в атоме и объясняет Периодическую систему элементов Д.И. Менделеева.