Вязкость воды при различных температурах
| t, °С | ||||||||||
| η•106 кг/м·с | ||||||||||
| t,°C | ||||||||||
| η ·106 кг/м·с |
Таблица 15.5
Кинематическая вязкость некоторых жидкостей при 20° (HadgmanC.D., 1965)
| Среда | Вязкость, ПЗ | Плотность, г/см3 | Кинематическая ВЯЗКОСТЬ, СМ2/С |
| Воздух | 1,8•10 -4 | 1,3 • Ю-3 | 0,14 |
| Вода | 0,010 | 1,00 | 0,010 |
Вода препятствует продвижению пловца. В гидродинамике для расчета движения жидкости используют число Рейнольдса. Число Рейнольдса — это безразмерная величина 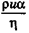 , где
, где 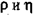 — плотность и вязкость жидкости, и — скорость ее движения относительно тела и а — некоторая длина.
— плотность и вязкость жидкости, и — скорость ее движения относительно тела и а — некоторая длина.
Правило, согласно которому строение потока около тел одной и той же формы одинаково, если одинаково число Рейнольдса, неприменимо в тех случаях, когда речь идет о поведении жидкости около ее свободной поверхности.
Число Рейнольдса удобно выражать как 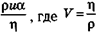 величина, называемая кинематической вязкостью.
величина, называемая кинематической вязкостью.
Во многих случаях трудно измерять силы, которые действуют на тело, движущееся в жидкости. В этой связи для экспериментов используют аэродинамические и гидродинамические трубы.
Лобовое сопротивление. При движении какого-нибудь тела в жидкости, на него действует сила, задерживающая его движение. Эту силу называют лобовым сопротивлением. Величина ее зависит от природы жидкости и от размеров, формы и скорости движущегося тела.
Как показали эксперименты в аэродинамических трубах, лобовое сопротивление тела или различных тел одной и той же формы можно определить по формуле 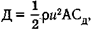 где Д — лобовое сопротивление, р — плотность жидкости, и — скорость движения жидкости относительно тела, А — характеристическая площадь и Сд — величина, называемая коэффициентом лобового сопротивления, которая зависит от формы тела и от числа Рейнольдса.
где Д — лобовое сопротивление, р — плотность жидкости, и — скорость движения жидкости относительно тела, А — характеристическая площадь и Сд — величина, называемая коэффициентом лобового сопротивления, которая зависит от формы тела и от числа Рейнольдса.
К сожалению, не существует единого определения А, которое было бы удобным при любой форме тела. Используются следующие площади:
1) лобовая площадь, т. е. площадь проекции тела на плоскость, перпендикулярно направлению потока. В случае цилиндра, имеющего высоту h и радиус г, лобовая площадь будет равна πr2, если ось цилиндра параллельна потоку, и 2rh, если она перпендикулярна ему;
2) площадь наибольшей проекции, т. е. проекции по тому направлению, по которому площадь ее будет наибольшей; эту величину используют, когда имеют дело с обтеканием профиля крыла; по сравнению с лобовой площадью она имеет то преимущество, что не изменяется при наклоне профиля;
3) суммарная поверхность тела. Следует помнить, что в случае тонкой пластинки это будет суммарная площадь обеих ее сторон.
Если есть сомнения, то важно указать, какая именно из этих площадей была использована при вычислении коэффициента С
На рис. 15.34 приведены кривые зависимости коэффициента лобового сопротивления Сд от числа Рейнольдса для тел различной формы.
Все коэффициенты были вычислены на основе лобовой площади.
Число Рейнольдса для всех тел, кроме диска, определялось обычным способом по длине, измеренной в направлении потока; для диска же его определяли по диаметру, хотя он расположен перпендикулярно потоку.
В связи с отсутствием работы по лобовому сопротивлению у пловцов, мы приводим данные Т.О. Lang, K.S. Norris (1966), R. Alexander (1968) полученные при изучении дельфинов. Было найдено, что при коротких «бросках» дельфин может развивать скорость до 830 см/с (около 16 узлов), а со скоростью 610 см/с (около 12 узлов) способен плыть примерно в течение 1 мин. Дельфин (Turbiopsgilli) имел длину 191 см, так что число Рейнольдса при первой из этих скоростей составляло 830·191 /0,01 = 1,6·107. Профиль дельфина хорошо обтекаем. Кожа очень гладкая и лишена волос. Все указывает на малую величину лобового сопротивления.
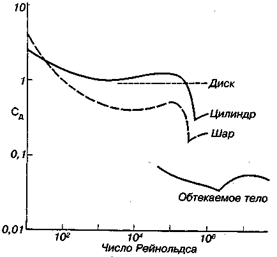
Рис. 15.34.Зависимость коэффициента лобового сопротивления от числа Рейнольдса для диска, расположенного перпендикулярно направлению своего движения; для удлиненного цилиндра, движущегося перпендикулярно своей оси; для шара и для тела обтекаемой формы, движущегося вдоль своей оси (по Р. Александер, 1970)
Попробуем оценить величину лобового сопротивления для дельфина, плывущего со скоростью 830 см/с и мощность, развиваемую его мышцами. Лобовая площадь у дельфина длиной 191 см, вероятно, составляет около 1100 см2. Коэффициенты лобового сопротивления для обтекаемых тел при числе Рейнольдса около 1,6-107 близки к 0,055. Подставив эти величины в уравнение
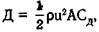 мы найдем, что лобовое сопротивление у нашего дельфина составляет примерно 1 /2 (830)2·1100·0,055 = 2,0-107 дин. Мощность равна сопротивлению, умноженному на скорость, т. е. в данном случае 830·2,0·107 эрг/с, или 1660 Вт. Однако от мышц требуется большая мощность, так как КПД дельфина при плавании не может достигать 100%; поэтому она едва ли могла быть меньше 2000 Вт. Дельфин весит 89 кг, из которых на долю участвующих в плавании мышц приходится, вероятно, около 15 кг. Таким образом, мощность мышц должна составлять примерно 130 Вт/кг. Это в 3 раза больше максимальной мощности, которую могут развивать мышцы человека при работе на велоэргометре.
мы найдем, что лобовое сопротивление у нашего дельфина составляет примерно 1 /2 (830)2·1100·0,055 = 2,0-107 дин. Мощность равна сопротивлению, умноженному на скорость, т. е. в данном случае 830·2,0·107 эрг/с, или 1660 Вт. Однако от мышц требуется большая мощность, так как КПД дельфина при плавании не может достигать 100%; поэтому она едва ли могла быть меньше 2000 Вт. Дельфин весит 89 кг, из которых на долю участвующих в плавании мышц приходится, вероятно, около 15 кг. Таким образом, мощность мышц должна составлять примерно 130 Вт/кг. Это в 3 раза больше максимальной мощности, которую могут развивать мышцы человека при работе на велоэргометре.
Лобовое сопротивление — не единственная гидродинамическая сила, действующая на тела, которые движутся в жидкости или находятся в потоке. По определению оно имеет то же направление, что и скорость движения жидкости относительно тела. Когда симметричное тело движется вдоль своей оси симметрии, действующая на него гидродинамическая сила направлена прямо и представляет собой лобовое сопротивление. Но когда симметричное тело движется под некоторым углом к оси симметрии, гидродинамическая сила действует под углом к его пути. Ее можно разложить на две составляющие, одна из которых направлена назад и представляет собой лобовое сопротивление, а другая действует под прямым углом к первой.
Энергетика пловца. Когда человек плывет, он сообщает некоторое количество энергии воде, чтобы продвинуться (проплыть) в ней. Это создает волну, которая в конечном счете потеряет всю сообщенную ей энергию в виде тепла, и поверхность воды снова станет спокойной. Затраченная таким образом при плавании энергия представляет собой совершенную работу плюс тепло, потерянное телом пловца.
Лыжный спорт
На лыжных гонках происходит сочетание свободного скольжения, отталкивания лыжами и палками от снега, маховых движений рук и ног и броска (перемещения) тела вперед-вверх (рис. 15.35).
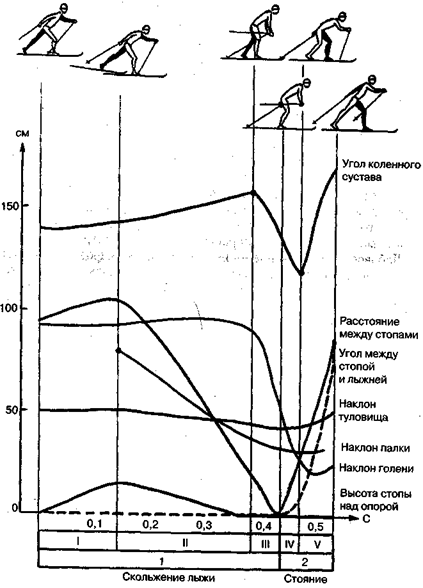
Рис. 15.35.Фазы попеременного хода на лыжах (по Х.Х. Гроссу)
Свободное скольжение (фаза I) происходит при тормозящем воздействии трения лыжи по снегу и незначительном сопротивлении воздуха. Чтобы меньше терять скорость, нельзя делать резких движений (рукой или ногой) направленных вверх-вперед. Свободное скольжение заканчивается постановкой палки на снег.
Начинается фаза скольжения с выпрямлением опорной ноги (фаза II). Увеличивая наклон туловища и нажим на палку лыжник стремится увеличить (повысить) скорость скольжения лыжи.
Подседание начинается еще (уже) при скольжении лыжи (фаза III), которая при энергичном разгибании опорной ноги в коленном и тазобедренном суставах быстро теряет (гасит) скорость и останавливается. Подседание, начатое в фазе III, продолжается и завершается в фазе IV, сопровождаемое выпадом — движением переносной ноги вперед. С окончанием подседания начинается выпрямление толчковой ноги в коленном суставе (фаза V), сопровождаемое завершающимся выпадом.
Следует отметить, что с повышением скорости передвижения изменяется ритм скользящего шага (сокращается время отталкивания лыжей; подседание и выпрямление толчковой ноги делаются быстрее).
Основой лыжной техники является попеременный шаг с постановкой палок при каждом шаге. Он соответствует нормальному бегу, который с помощью лыж переходит в ритмичное скольжение. Толчок к скольжению дается мощным отталкиванием соответствующей ноги от снежного основания и толчок палками. Отталкивание всегда начинается тогда, когда обе ноги находятся приблизительно рядом. Однако эффективным оно бывает, если лыжа в этот момент имеет достаточное трение со снежным основанием благодаря правильной смазке. В то время как левая нога отталкивается, правая становится скользящей. При этом масса тела переходит с отталкивающейся ноги на скользящую. Лыжник-гонщик скользит преимущественно на одной лыже. Только во время короткого промежутка отталкивания ногой обе лыжи одновременно касаются снега.
Велосипедный спорт
Велосипедист должен преодолеть три силы сопротивления (рис. 15.36):
— силу сопротивления встречного потока воздуха;
Рис. 15.36.
Посадка велогонщика

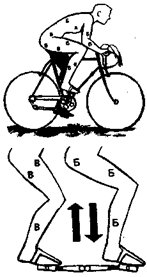
Рис. 15.37.Мышцы, участвующие в процессе езды велосипедиста:
А — дыхательная мускулатура, Б — мышцы, участвующие в перемещении педали вниз,В — мышцы, участвующие в перемещении педали вверх
— силу трения качения (см. рис. 6.5, табл. 6.2);
— сталкивающую силу при подъеме на гору.
Внешним силам сопротивления спортсмен противопоставляет силу своих мышц, правильную посадку и пр.
На рис. 15.37, показаны мышцы, работающие в процессе нажимания на педали.
Главное препятствие для преодоления дистанции — встречный поток воздуха. Чем выше скорость, тем больше сила сопротивления встречного потока воздуха. Сопротивление воздуха можно уменьшить несколькими способами.
Сила сопротивления воздушного потока fb зависит от следующих факторов:
А — величина поверхности сопротивления, которую можно изменить посадкой;
Кc — коэффициент сопротивления, который зависит от обтекаемости фигуры велосипедиста и от величины поверхности одежды;
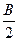 — плотность воздуха, которая на равнине примерно постоянна, а в горных районах несколько ниже;
— плотность воздуха, которая на равнине примерно постоянна, а в горных районах несколько ниже;
V2 — квадрат скорости. Сопротивление воздуха растет, следовательно, не пропорционально скорости велосипедиста, а гораздо сильнее. 
При встречном ветре эта сила увеличивается, при попутном — уменьшается, что дает уменьшение или увеличение скорости. Для уменьшения силы сопротивления встречного потока воздуха необходимо сесть так, чтобы поверхность (А), которую вы занимаете, была относительно небольшой. В спринте — предпочтительно совершать (принимать) горизонтальную посадку. Для уменьшения сопротивления воздуха используют (применяют) специальные шлемы и обтекаемые костюмы (комбинезоны).
На скорость перемещения велосипедиста влияет сила трения качения (трение шин о покрытие шоссе). Чем тяжелее велосипедист, тем больше трение качения, а также чем толще шины и меньше они накачаны — тем больше трение качения. Влияют на скорость велосипедиста также качество покрытия шоссе, размер колес.
Сила трения качения Fmр зависит от следующих факторов:
— Fн — нормальная сила соответствует весу спортсмена с велосипедом, если он направлен перпендикулярно к поверхности, по которой происходит перемещение;
— r — радиус колес;
— f — расстояние между теоретической точкой опоры шины и фактической точкой встречи шины с поверхностью, по которой происходит перемещение. Отсюда имеем формулу:
Посадка велосипедиста во  время шоссейной гонки должна быть максимально обтекаемой и в то же время не мешать работе внутренних органов (рис. 15.38). Посадка велосипедиста на подъеме может быть такой: 1) кисти рук на тормозных рычагах; 2) кисти в центре руля, обхватывают его снизу; 3) положение, при котором переносится центр тяжести тела.
время шоссейной гонки должна быть максимально обтекаемой и в то же время не мешать работе внутренних органов (рис. 15.38). Посадка велосипедиста на подъеме может быть такой: 1) кисти рук на тормозных рычагах; 2) кисти в центре руля, обхватывают его снизу; 3) положение, при котором переносится центр тяжести тела.
Во время подъема скорость небольшая, решающую роль приобретает сталкивающая сила, а сопротивлением встречного воздушного потока можно пренебречь.

Рис. 15.38. Посадка велосипедиста при шоссейных гонках
Для сталкивающей силы (F.) решающими являются следующие факторы:
G — суммарный вес спортсмена с велосипедом;
l — длина пути;
h — высота подъема на 100 м пути

Чем больше вес спортсмена с велосипедом и крутизна подъема (например, при перепаде высот 6 м на 100 м подъема — 6%), тем больше сталкивающая сила.
При выполнении поворота возникает центробежная сила, величина которой зависит от трех факторов: 1) чем больше скорость и вес спортсмена с машиной и чем меньше радиус закругления, тем больше центробежная сила; 2) для противодействия центробежной силе следует наклониться вместе с велосипедом в сторону закругления. На рис. 15.39 показаны центробежная сила и направление взаимодействия других сил, возникающих при прохождении виража; 3) в зависимости от формы виража и скорости необходимо наклониться так, чтобы угол между велосипедом и поверхностью трека составлял от 70° до 110°. В идеальном варианте он должен быть равен 90°.
Но в некоторых ситуациях гонщик должен ехать по треку медленно, например, в спринте, парной групповой гонке и т. д. В этих случаях при слишком маленькой скорости можно упасть, так как колесо соскользнет вниз. При медленной езде или попытке полностью остановиться центробежные силы незначительны или даже равны нулю, а значит наклоняться на вираже нельзя.
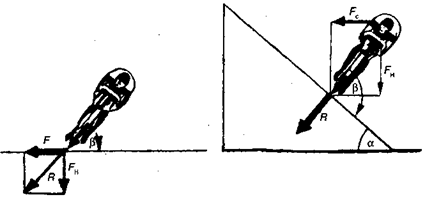
Рис. 15.39.Силы, действующие на велосипедиста при прохождении виража:F— центробежная сила, FH — нормальная сила, R — результирующая, α — угол крутизны трека, Fc — сталкивающая сила, β — угол наклона
Преимущество езды сверху заключается в возможности использовать сталкивающую силу (Fc) для значительного увеличения скорости. Сталкивающая сила прямо пропорциональна высоте кривой (h) и весу велосипедиста с машиной (G).

Чем тяжелее спортсмен и чем выше располагается он на вираже, тем больше сталкивающая сила. Преимущество будет на стороне гонщика, если при выходе из финишного виража он окажется в верхней его части на одном уровне с соперником.
Прыжки
При прыжках обе ноги после сгибания в главных своих суставах (тазобедренных, коленных, голеностопных) выпрямляются быстрым и сильным сокращением разгибателей и отрываются от земли толчком, который передается телу. При этом прыжок или совершается на месте — тело поднимается в вертикальном направлении, или же телу сообщается поступательное движение вперед и вверх (рис. 15.40).
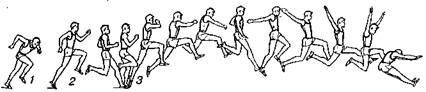
Рис. 15.40. Прыжки в длину с разбега
Прыжки в длину с разбега. Чем быстрее человек бежит, тем дальше он может прыгнуть. Кинетическая энергия бега может также при известных обстоятельствах использоваться для прыжков в высоту. На этом принципе основаны прыжки с шестом (G.H. Dyson, 1962).
Перед прыжком центр тяжести уже находится на высоте около 90 см над землей, а во время прыжка оказывается лишь немного выше планки. Например, при использовании метода «вестерн-ролл» центр тяжести (ЦТ) тела может подниматься над планкой на высоту около 15 см (G.H. Dyson, 1962).
Когда человек прыгает «с места», каждая из участвующих в этом акте мышц сокращается только один раз. Максимальная сила, развиваемая мышцей, пропорциональна площади ее поперечного сечения. Возможное укорочение мышцы пропорционально ее длине. Следовательно, работа, которую она может совершить при одиночном сокращении, пропорциональна произведению ее длины на площадь поперечного сечения, т. е. ее объему. Мышцы одинакового объема (или веса) способны совершать одинаковую работу. Представим теперь животное, масса которого т, а мышцы, участвующие в прыжке, — масса т'. Пусть эти мышцы при одиночном сокращении способны совершать работу Km'. Эта работа равна кинетической энергии, которую приобретает тело животного при отрыве от земли:

где и — скорость в момент отрыва. Если бы животное прыгнуло вертикально, оно поднялось бы на высоту 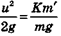 . В случае прыжка под углом 45° оно опустилось бы на расстоянии
. В случае прыжка под углом 45° оно опустилось бы на расстоянии 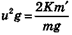 от начального пункта. Поэтому можно ожидать, что разные животные, у которых отношения массы используемых при прыжке мышц к общей массе тела равны (т. е. равны величины
от начального пункта. Поэтому можно ожидать, что разные животные, у которых отношения массы используемых при прыжке мышц к общей массе тела равны (т. е. равны величины 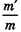 ), способны прыгать на одинаковую высоту и одинаковое расстояние независимо от размеров тела.
), способны прыгать на одинаковую высоту и одинаковое расстояние независимо от размеров тела.
Попробуем теперь исходить из иного предположения относительно мышц. Будем считать, что способность совершать прыжки ограничивается максимальной мощностью, которую могут развить мышцы, и что единица массы мышечной ткани может развивать мощность KI. Пусть за время от начала сокращения мышц до момента отрыва ног от земли центр тяжести (ЦТ) животного перемещается на расстояние l. Для большинства животных l будет немного меньше длины ног. Мы уже знаем, что к моменту отрыва от земли должна быть совершена работа 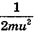 . Чтобы найти необходимую мощность, нам нужно разделить эту работу на время t, за которое она производится. Проходя путь / за время t, животное увеличивает свою скорость от 0 до U. Предположим, что ускорение постоянно и используем уравнение. Тогда получим
. Чтобы найти необходимую мощность, нам нужно разделить эту работу на время t, за которое она производится. Проходя путь / за время t, животное увеличивает свою скорость от 0 до U. Предположим, что ускорение постоянно и используем уравнение. Тогда получим
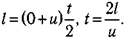 (15.8)
(15.8)
Мощность, необходимая для совершения работы 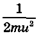 за это время, составляет
за это время, составляет 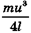 , а мощность, которую могут развивать используемые при прыжке мышцы, равна Km1. Отсюда
, а мощность, которую могут развивать используемые при прыжке мышцы, равна Km1. Отсюда
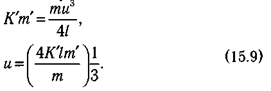
Если животное отрывается с этой скоростью от земли вертикально вверх, оно достигает высоты. 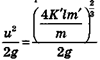 Если же оно отрывается под углом 45°, оно прыгнет на расстояние
Если же оно отрывается под углом 45°, оно прыгнет на расстояние 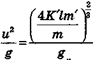 .
.
Для животных разной величины, но с одинаковой относительной массой мышц, используемых при прыжке, наибольшая высота и длина прыжков должна быть пропорциональна пути ускорения (т. е. пути, на котором скорость равномерно возрастает от 0 до и) в степени 2/3. Спортсмен может прыгнуть в длину с разбега на расстояние до 8 м. С помощью рассмотренных выше формул мы можем приблизительно определить начальную скорость, с которой спортсмен должен оторваться от земли (скорость отрыва). В случае оптимального угла отрыва от земли в 45° необходимая скорость определяется
из уравнения 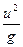 = 800, отсюда
= 800, отсюда
и = 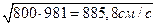 (15.10)
(15.10)
Следовательно, скорость отрыва от земли составляет 885,8 см/с без учета сопротивления воздуха.
Если угол отрыва равен 55°, а дальность прыжка та же, то спортсмен должен отрываться от земли со скоростью, которую можно найти из уравнения
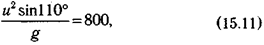
значит,
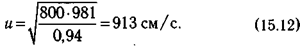
Если бы при этом ускорение было постоянным, его можно было бы вычислить по формуле:
(913)2=2a·4, (15.13)
а = 104196 см/сек2.
Если масса тела спортсмена равна m граммов, то для того, чтобы придать ему такое ускорение, понадобилась бы сила 104 196 m дин. Одна дина — это сила, необходимая для того, чтобы сообщить массе в 1 г ускорение, равное 1 см/с2 (т. е. увеличить ее скорость на 1 см/с за каждую секунду).
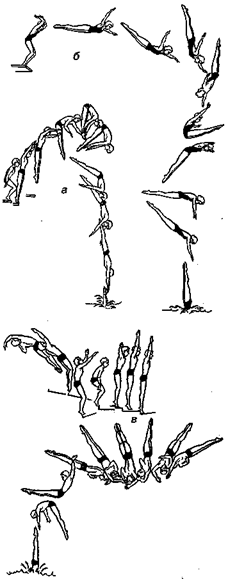
Рис. 15.41. Прыжки в воду.
а — из передней стойки полуоборот вперед согнувшись; - из передней стойки полтора оборота вперед «летом» согнувшись; в — полтора оборота назад с двумя с половиной винтами
Прыжки в воду
Прыжки в воду относятся к технико-композиционным видам спорта и включают в себя прыжки с трамплина и с вышки. Прыжки выполняются из передней или задней стойки, с вращательными движениями, винтами, прыжки из стойки на кистях и т. д. (рис. 15.41).
Главным элементом техники прыжка с трамплина и вышки является разбег, толчок, фаза полета и вход в воду.
Выполнение всего прыжка зависит от толчка. При этом направлением толчка определяется последующая траектория полета, которую спортсмен не сможет изменить в ходе фазы полета. Фаза полета начинается в момент отрыва ног от доски или от площадки и заканчивается касанием поверхности воды. Фаза полета вводится толчком, который определяет оптимальную траекторию полета и выполнение движений. Основным требованием к входу в воду является вертикальное положение погружаемой части тела по отношению к поверхности воды для того, чтобы войти в воду почти без брызг.
Толкание ядра
Последовательность движений при толкании ядра можно описать, разделив упражнение на три фазы: скачок, поворот туловища и выпрямление руки (рис. 15.42). Дальность полета ядра зависит от траектории ядра, от стартовой точки до момента выпуска ядра, скорости скачка (т. е. в первой фазе упражнения), скорости выпуска ядра выпрямленной рукой, высотой выпуска ядра, массы спортсмена и др.
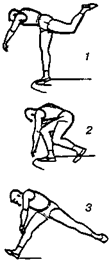

Рис. 15.42.
Толкание ядра
(1—6 —фазы
толкания ядра)
S. Francis (1948) выявил, что средняя высота выпуска ядра была на 152 мм выше среднего роста обследованных спортсменов (183 см).
Тяжелая атлетика
Тяжелая атлетика — вид спорта, требующий высокой точности воспроизведения упражнения как системы движений. Состязания по подъему (поднятию) тяжестей (штанги) — относятся к таким видам спорта, в которых решающую роль играют в одинаковой мере физическая сила и техника.
Упражнения для развития силы довольно разнообразны, их можно выполнять при помощи штанги, гирь, гантелей, тяговых снарядов (тренажеров) и т. д. Эти упражнения хорошо зарекомендовали себя во многих видах спорта и служат спортсменам для развития силы и выносливости (скоростно-силовых качеств). Упражнения с большими тяжестями применяются в основном для развития максимальной силы, а при помощи упражнений в высоком темпе развивается скоростная сила, т. е. скоростно-силовые качества.
Целью штангиста является подъем штанги при одновременном сохранении равновесия тела на маленькой площади опоры в период движений, связанных с подъемом. При этом движения различаются от фазы подъема к опорной фазе. На определенное время требуется относительно небольшая сила для воздействия на штангу, для того чтобы совершить необходимые изменения в устойчивости ног при удержании штанги. Сила применяется в вертикальном направлении, но, поскольку штанга описывает кривую в виде буквы S на уровне корпуса тела, в действие могут вступить также и горизонтальные силы. Ускорение штанги зависит от величины силы, которая воздействует на нее, а также от массы снаряда. Чем меньше масса снаряда, тем больше скорость при равном применении силы и наоборот. Достигнутая максимальная скорость является решающей для так называемой тяговой высоты штанги.
Силы, воздействующие на систему «штанга — корпус», должны использоваться в основном периоде тяговой фазы только для необходимых перегруппировок частей корпуса тела от фазы подъема до подрыва. Воздействие мышечной силы на штангу обусловливает эластичную деформацию штанги. Возникают так называемые эластичные силы в снаряде. Они способствуют ускорению штанги и надежному перемещению ее. Штангист должен для использования эластичного действия штанги выработать определенное чувство ритма в период тренировок.
При перемещении штанги спортсмен достигает и преодолевает разные силы: а) вес штанги (сила тяжести); б) сила инерции штанги, которая зависит от массы и от скорости штанги; в) сила тяжести и сила инерции собственного тела.
Эти факторы являются решающими критериями для оценки техники и силы спортсмена. Освоение техники упражнений способствует выработке правильной осанки.
К важнейшим упражнениям относятся приседания и наклоны со штангой на плечах (рис. 15.43). На рис. 15.44 показано обучение правильной (нормальной) осанке при выполнении упражнений с отягощениями.
Координация движений тяжелоатлета затрудняется в результате некоторых факторов:
1. Трудности при подъеме штанги предельного веса — это комплексный фактор: а) атлет все время вынужден менять вес поднимаемой штанги, что заставляет изменять координацию мышечных напряжений; б) атлет не имеет возможности многократно повторять рывок и толчок с соревновательными вариантами веса штанги в связи с предельным характером нагрузки.
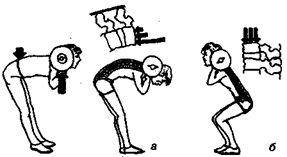
Рис. 15.43.Нагрузка на позвоночник при поднятии штанги: а — неправильно; б — правильно
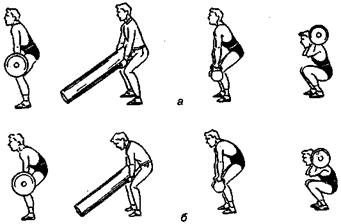
Рис. 15.44.Тренировка с отягощением: а — правильно; б — неправильно
2. Значительные сдвиги в силовой подготовленности тяжелоатлетов в процессе тренировки заставляют соответственно менять технику подъема штанги в связи с большими изменениями внутренних сил в системе «атлет — штанга».
3. Кратковременность всего упражнения или отдельных его частей ограничивает возможность текущих коррекций движений на основе функционирования обратной связи.
Для развития (тренировки) силы тех или иных мышц важным является исходное положение спортсмена. На рис. 15.45 показано приседание спортсмена со штангой весом 50 кг на плечах в одной из поз и момент силы, действующей в отдельных суставах будет различен (табл. 15.6), хотя сила действия штанги везде одна и та же — 50 кг.
Таблица 15.6
Вращательные моменты силы, создаваемые действием мышц в суставах нижних конечностей при приседании со штангой весом 50 кг на плечах (ньютонометры, вес спортсмена 75 кг) (по S. Plagenhoef, 1971)
| Положение тела | Суставы | ||
| Тазобедренный | Коленный | Голеностопный | |
| А | +185 | +70 | +25 |
| Б | +76 | +175 | +4 |
| В | +185 | +10 | +38 |
| Г | +218 | —22 | +22 |
Знак (+) означает, что момент силы направлен на разгибание в суставе, знак (—) указывает действие момента в направлении сгибания.
Таким образом, при одной и той же силе действия в разных позах их величины сил и силовых моментов, действующих в отдельных суставах, могут быть различными. При неправильно выбранной позе момент силы, действующей на позвоночник и суставы может быть критическим и вызвать травму (рис. 15.45 а, б, г), а если упражнения со штангой выполняются длительно, с большим количеством повторений, то возникают заболевания опорно-двигательного аппарата (ОДА). При правильной технике выполнения упражнения этого не происходит (см. рис. 15.43, б, 15.45, в).
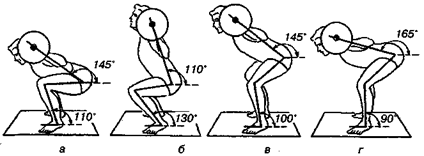
Рис. 15.45.Варианты поз спортсмена при приседании со штангой 50 кг
на плечах (по S. Plagenhoef, 1971).
В каждом из этих положений сила действия одинакова (= 50 кг), а вращательные моменты силы в суставах различны
Дата добавления: 2015-11-28; просмотров: 1994;
