Расчет величины депрессии естественной тяги гидростатическим методом
Выделим в столбе воздуха вертикальной высоты Нэлемент dz,ограниченный сечениями 1-1 и 2-2, так чтобы в пределах выделенного элемента объемный вес воздуха 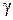 =const (рис.6.4). Тогда прирост гидростатического давления на высоте dz выразится в виде
=const (рис.6.4). Тогда прирост гидростатического давления на высоте dz выразится в виде
dp= 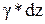 (7.5)
(7.5)
Задача состоит в определении давления р1или приращения давления 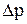 на глубине Нпри граничных условиях:
на глубине Нпри граничных условиях:
z=0; P=P0; z=H; р=р1.
   |
Рис.7.4. - Схема к расчету приращения давления
Для решения уравнения (7.5) необходимо знать зависимость 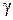 (z) или
(z) или 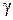 (Р). Обычно находят зависимость объемного веса от давления, используя уравнение газового состояния
(Р). Обычно находят зависимость объемного веса от давления, используя уравнение газового состояния
pV=Rг Т (7.6)
где V = 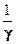 удельный объем воздуха, м3/кг;
удельный объем воздуха, м3/кг;
Rг - газовая постоянная, равная для сухого воздуха 29.27 м/град;
Т - абсолютная температура 0K.
Из равенства (7.6) получим
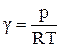 (7.7)
(7.7)
Уравнение (7.5) с учетом (7.7) принимает вид
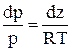 (7.8)
(7.8)
Заменяя с некоторым приближением в уравнении (7.8) Т на Т 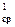 -среднюю температуру воздуха в стволе №1 в пределах от z=0 до z=Ни интегрируя от ро до р1 и от 0 до Н, получим
-среднюю температуру воздуха в стволе №1 в пределах от z=0 до z=Ни интегрируя от ро до р1 и от 0 до Н, получим
ln 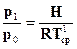 (7.9)
(7.9)
Из равенства (7.9) определяем давление р1 на голубине Н.
р1=р0 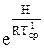 (7.10)
(7.10)
Приращение давления в стволе №1 будет
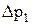 =р1-р0=р0(
=р1-р0=р0(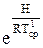 -1) (7.11)
-1) (7.11)
Аналогичным образом, рассматривая ствол №2, определим давление в точке 2 на глубине Ни приращение давления 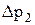
р2=р0 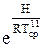 (7.12)
(7.12)
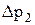 =р2-р0=р0(
=р2-р0=р0(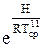 -1) (7.13)
-1) (7.13)
где Т 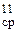 - средняя температуру воздуха в стволе №2 в пределах от z=0 до z=Н0K.
- средняя температуру воздуха в стволе №2 в пределах от z=0 до z=Н0K.
Для расчета депрессии естественной тяги необходимо по формулам (7.11) (7.13) определить давление р1 и р2в нижних частях сообщающихся столбов воздуха равной высоты Н, отсчитываемой от уровня равного атмосферного давления. Для схемы изображенной на рис.7.4
hе=р1-р2 (7.14)
или с учетом равенств (7.11), (7.13)
hе= 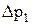 -
- 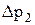 (7.15).
(7.15).
Дата добавления: 2016-01-26; просмотров: 988;
