Закон сохранения массы. Движение воздуха в шахте подчиняется законам сохранения массы и энергии

Движение воздуха в шахте подчиняется законам сохранения массы и энергии

Закон сохранения массы применительно к движению воздуха формулируется следующим образом: масса любого объема воздуха остается постоянной в процессе его движения.

Если в потоке выделить элементарный объем ω, достаточно малый, чтобы плотность воздуха в нем можно было считать постоянной, то закон сохранения массы можно записать так:

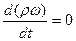(3.16)

где ρω – масса выделенного объема

Через проекции скорости потока в рассматриваемой точке на оси координат этот закон запишется так:

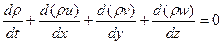(3.17)

где u, v,w- соответственно, проекции скорости в рассматриваемой точке потока на оси x, y, z системы координат.

Для стационарного движения плотность, скорость, давление, температура в фиксированной точке потока не изменяются, тогда 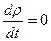и равенство (3.17) запишется так:

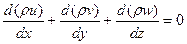(3.18)

а при постоянной плотности потока ρ=const

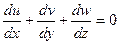(3.19)

В выработке постоянного сечения v=w=0 тогда из уравнения (3.19) найдем, что u=const, т. е. скорости движения воздуха в сходственных точках постоянны. Из уравнения (3.19) также следует, что увеличение скорости в одном направлении должно вызывать уменьшение ее в другом направлении, так как сумма членов в его левой части будет равна нулю тогда, когда одни из них будут положительны (ускорение течения), другие отрицательными (замедление).

Для случая стационарного движения воздуха в выработке из уравнения (3.16) получим

М=const (3.20)

Выразим массовый расход воздуха в выработке в виде

М=ρ*Q (2.21)

где Q-объемный расход воздуха в выработке.

Тогда для изотермического процесса (т.е. при ρ=const) из выражения (2.21) получим

Q=const (2.22)

Из выражения (2.22), называемогоуравнением расхода, следует, что для стационарного движения объемный расход воздуха в выработке постоянный.

При разветвлении потока уравнение (2.22) примет вид

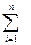Q_i=0 (2.23)

где i – номер потока; n – число потоков в разветвлении.