ЛІТЕРАТУРА ДОДАТКОВА. В якості приклада використання отриманих залежностей нижче наведено приклад інженерного розрахунку гвинтових циліндричних пружин

В якості приклада використання отриманих залежностей нижче наведено приклад інженерного розрахунку гвинтових циліндричних пружин, які широко розповсюджені у техніці (ресорах вагонів, в клапанах, інших механізмах сучасних транспортних засобів).

Розглянемо пружину (рисунок 9 а), виготовлену зі стального круглого прутка; 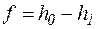– осідання пружини під дією сили 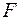. Розрахункові параметри: 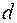– діаметр прутка; 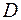– середній діаметр витків; 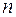– кількість витків.

Згідно з методом перерізів, розглядаючи рівновагу верхньої частини пружини (рисунок 9 б), визначаємо внутрішні силові фактори: поперечну силу 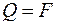та крутний момент 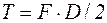. Звідки випливає, що у поперечному перерізі витка діють тільки дотичні напруження зсуву та кручення.

Насправді, при цьому ми нехтували малими за величиною подовжньою силою та згинальним моментом. Помилка при такому розрахунку буде тим більша, чим більше кут підйому витка .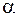

Максимальні сумарні напруження діють у крайній точці перерізу витка на внутрішньому радіусі пружини.

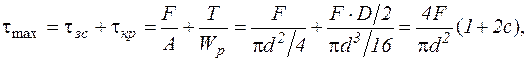(25)

де 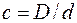– індекс пружини.

Рисунок 9 – Розрахункова схема циліндричної гвинтової пружини

Аналіз свідчить, що напруження зсуву 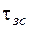складають лише 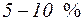від напружень кручення 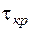і можуть при грубих розрахунках не враховуватися.

Більш точний результат дає формула, яка враховує кривизну витків за допомогою спеціального поправочного коефіцієнту 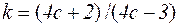; тоді формулу для розрахунку пружини на міцність можна записати у вигляді

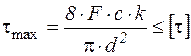. (26)

При визначенні осідання 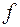пружини будемо враховувати тільки кручення витого прутка, бо інші види деформування вносять дуже малий вклад. Скористаємось енергетичним підходом, згідно з яким робота зовнішньої сили 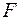на осіданні 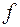переходить у потенційну енергію 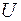деформованої пружини, яка дорівнює роботі крутного моменту 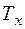на куті 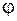закручення прутка (рисунок 6.3).

Запишемо потенційну енергію 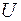з урахуванням формули (6.8) для 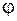, величини крутного моменту 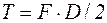, довжини прутка 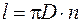та формули (5.8) для :

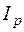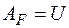. (27)

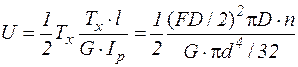. (28)

Після підстановки виразів для 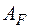і 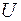у (6.15) та деяких скорочень отримаємо остаточну розрахункову формулу для осідання пружини

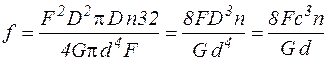. (29)

З (6.17) можливо підібрати такі параметри пружини, щоб отримати для заданого навантаження бажане осідання пружини.

Питання для самоконтролю:

1. Як обчислити величину осідання циліндричної гвинтової пружини при стиску?

1. Як зміняться дотичні напруги в пружині /за інших однакових величин/, якщо діаметр дроту збільшити /зменшити/ удачі?

Заняття № 51