Понятие информация. Формы представления информации. Свойства информации.

Информация — это сведения об объектах и явлениях окружающего мира, уменьшающие степень неопределённости знаний об этих объектах или явлениях/

«информация» — сведения, передаваемые людьми устным, письменным или другим способом (с помощью условных сигналов, технических средств и т. д.)

Эффективность использования информации связана с такими её свойствами, как актуальность, доступность (понятность), достоверность, репрезентативность, адекватность и полнота.

Рассмотрим эти свойства более подробно.

Актуальность информации определяется тем, насколько важны для человека или общества данные сведения, могут ли они быть использованы в конкретной ситуации для решения проблемы.

Это свойство во многом зависит от интервала времени, прошедшего с момента появления данной информации, а также от того, насколько быстро изменяется ситуация.

Таким образом, своевременность информации предполагает её поступление не позже заранее назначенного момента времени, согласованного со временем решения поставленной задачи.

Только актуальная, вовремя полученная информация может принести пользу людям. Недаром прогноз погоды сообщают накануне, а не в тот же день.

В соответствии с этим же правилом учёные стараются найти более надёжные способы предупреждения о землетрясениях, ураганах и других стихийных бедствиях.

Доступность информации обеспечивается за счёт её преобразования в понятную форму. При этом одну и ту же информацию можно представить в разной форме в зависимости от её получателя.

Информация становится понятной, если она выражена в той форме и тем языком, который воспринимает тот, кому она предназначена.

Достоверность информации определяется её свойством отражать состояние реально существующего объекта, процесса или явления. Недостоверная информация может привести к неправильному пониманию ситуации и, как следствие, к принятию неправильного решения.

Полнота (достаточность) информации означает, что она содержит минимальный, но достаточный для принятия правильного решения набор данных. О полноте информации можно говорить, когда какая-либо дополнительная информация об объекте будет уже избыточна.

Понятие полноты информации связано с её смысловым содержанием.

Как неполная, так и избыточная информация снижает эффективность решений, принимаемых человеком на её основе.

Адекватность информации — это соответствие образа, создаваемого с помощью полученной информации (информационной модели), реальному объекту, процессу или явлению. В реальной жизни вряд ли возможна ситуация, когда существует полная адекватность информации. Всегда присутствует большая или меньшая степень неопределённости. Степень адекватности информации реальному состоянию объекта тоже влияет на правильность решений, принятых человеком.

Репрезентативность информации связана с правильностью её отбора и формирования для адекватного отражения свойств объекта. Непременным условием определения свойства репрезентативности информации является поступление похожей информации из разных источников. Понятно, что полного совпадения по всем источникам информации никогда не будет. Однако если все сделано правильно, то полученная информация будет отражать самые важные характеристики объекта.

1. Информационные технологии. Этапы развития информационных технологий.

Информационная технология — это процесс, использующий совокупность средств и методов сбора, обработки и передачи данных для получения информации нового качества о состоянии объекта, процесса или явления.

Информационные технологии (ИТ) – это инструмент с помощью которого используются информационные ресурсы всего общества.

К настоящему времени прошло несколько эволюционных этапов развития информационных технологий. Смена этапов развития происходила в следствии научно-технического прогресса.

В истории становления ИТ выделяют следующие виды передачи и хранения информации: письменность, печать книг, телеграф, почта, телефонная связь, телевидение, компьютеры.

Самое важное место в истории развития ИТ занимают компьютеры и компьютерные сети. Глобальные и локальные и сети дали огромный толчек в развитии всему человечеству, предоставили возможность передачи мультимедийных сообщений на большие расстояния за минимальное количество времени.

Процесс развития компьютерных информационных технологий можно разделить на следующие этапы:

Первичный этап развития ИТ. Человек и ЭВМ могут взаимодействовать только с помощью машинных языков.

Доступ к ЭВМ имеют только профессионалы (1950-1960 гг.). Возникают первые операционные системы, появляетя многозадачность (1960-1970гг.).

Создаются ЭВМ небольшого размера, осуществляется интерактивное взаимодействие нескольких пользователей (1970-1980 гг.). Упор на создание способов взаимодействия пользователей с ЭВМ.

Появляются базы знаний (1980-1990гг.).

Повсеместное распространение компьютеров и объединение их в сеть интернет (с 1990 года по настоящее время).

Как видно из этапов перечисленных выше, за время появления первых ЭВМ они значительно увеличили свои возможности и стали общедоступными. Объемы информации формируемые в компьютерных системах растут с геометрической прогрессией.

В ходе технологического прогресса важнейшим национальным ресурсом является информация. Компьютерный прогресс зашел уже довольно далеко, но что же может ждать нас дальше?

В наши дни электронное моделирование, которое является неотъемлемым компонентом интеллектуальной деятельности человечества, привлекает все больше внимание в сфере ИТ. Сопоставление компьютерных алгоритмов с человеческим мозгом дало толчок к идеи создания нейрокомпьютера, который может обучаться. Нейрокомпьютер копирует поведение мозга человека. Он многократно ознакамливается с информацией, делает ошибки, анализирует их, корректирует и, наконец, выполняет задачу.

Можно только представить как изменится наша жизнь, если идея нейрокомпьютера перерастет в искусственный интеллект. Научно-технический прогресс продолжает естественную эволюцию человека.

На текущем этапе развития информационные технологии освобождают человека от рутинного интеллектуального труда и дает ему шанс открыть свои творческие возможности.

Этапы развития:

1 этап (до второй половиныXIX в.) — "ручная" информационная технология, инструментарий которой составляли: перо, чернильница, книга. Коммуникации осуществлялись ручным способом путем переправки через почту писем, пакетов, депеш. Основная цель технологии — представление информации в нужной форме.

2 этап(с концаXIX в.) — "механическая" технология, инструментарий которой составляли: пишущая машинка, телефон, диктофон, оснащенная более совершенными средствами доставки почта. Основная цель технологии — представление информации в нужной форме более удобными средствами.

3 этап (40 - 60-е гг.) — "электрическая" технология, инструментарий которой составляли: большие ЭВМ и соответствующее программное обеспечение, электрические пишущие машинки, копировальные аппараты, портативные диктофоны. Изменяется цель технологии — акцент начинает перемещаться с формы представления информации на формирование ее содержания.

4 этап(с начала 70-х гг.) — "электронная" технология, инструментарием которой становятся большие ЭВМ и создаваемые на их базе автоматизированные системы управления (АСУ) и информационно-поисковые системы (ИПС), оснащенные широким спектром базовых и специализированных программных комплексов. Акцент смещается в сторону формирования более содержательной информации.

5 этап(с середины 80-х гг.) — "компьютерная" технология, основным инструментарием которой является персональный компьютер с широким спектром стандартных программных продуктов разного назначения. На этом этапе происходит процесс персонализацииАСУ (создание систем поддержки принятия решения для разных специалистов).

2. Системы счисления и виды систем счисления.

Система счисления - это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами./ десятичную, двоичную, шестнадцатеричную/

Система счисле́ния — символический метод записи чисел, представление чисел с помощью письменных знаков.

В зависимости от способа изображения чисел системы счисления делятся на позиционные и непозиционные.

В позиционной системе счисления значение каждой цифры числа зависит от того, в каком месте (позиции или разряде) она записана. Например, меняя позицию цифры 2 в десятичной системе

счисления, можно записать разные по величине десятичные числа, например: 2; 20; 2000; 0,02 и т. д.

Позиция цифры в числе называется разрядом. Разряд числа возрастает справа налево, от младших разрядов к старшим.

В непозиционной системе счисления цифры не изменяют своего значения при изменении их расположения в числе. Примером непозиционной системы может служить римская система, в которой независимо от местоположения одинаковый символ имеет неизменное значение (например, символ X

в числе XXV).

В римской непозиционной системе счисления для каждого числа используется некоторый набор базовых символов (I,V,X,L,C,D и M), соответствующих числам

1,5,10,50,100,500 и 1000.

Остальные значения чисел получаются из базовых путем их сложения (например, XVII=17) или

вычитания (например, IX=9).

Недостатком римской системы является отсутствие формальных правил записи чисел и, соответственно, арифметических действий с многозначными числами. По причине неудобства и большой сложности в настоящее время римская система счисления используется там, где это действительно удобно: в литературе (нумерация глав), в оформлении документов (серия паспорта, ценных бумаг и др.), в декоративных целях на циферблате часов и в ряде других случаев.

Количество (р) различных символов, используемых для изображения числа в позиционной системе счисления, называется основанием системы счисления.

Основание показывает, во сколько раз изменяется количественное значение цифры при перемещении ее в младший или старший разряд.

Набор символов, используемый для обозначения цифр, называется алфавитом.

Так, например, алфавит двоичной системы счисления содержит всего два символа: 0 и 1, а алфавит шестнадцатеричной системы - 16 символов: десять арабских цифр и шесть латинских букв (0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F).

Любое число N в позиционной системе счисления можно представить в следующем виде:Np=±(ak−1⋅pk−1+ak−2⋅pk−2+...+a0⋅p0+a−1⋅p−1+...+a−m⋅p−m)

Такой вид записи числа называют развернутой формой записи числа,

где р - основание системы счисления;

ai - цифры, принадлежащие алфавиту данной системы счисления;

k - количество разрядов в целой части числа;

m - количество разрядов в дробной части числа.

Нижние индексы определяют местоположение цифры в числе (разряд):

- положительные значения индексов - для целой части числа;

- отрицательные значения индексов - для дробной части числа.

Свернутой формой записи числа называется запись в виде:

N=(ak−1ak−2...a1a0,a−1a−2...a−m)p

Например:- при р=10 в записи числа 2466,67510 в десятичной системе счисления k=3, m=3;- при р=2 в записи числа 1011,112 в двоичной системе k=3, m=2.

Свернутой формой записи чисел мы и пользуемся в повседневной жизни, ее называют естественной или цифровой.

Основанием позиционной системы счисления может быть любое натуральное число (например, 5, 21, 37). Во избежание путаницы справа от числа нижним индексом приписывают основание:

1011012, 3678, 3B8A16, 3AO37.

Десятичная система счисления

Основание: p=10.

Алфавит: 0,1,2,3,4,5,6,7,8,9.

Десятичная система счисления наиболее распространенная система счисления в мире. Используется при повседневном счете. Для записи чисел используются арабские цифры (0, 1, 2, 3, 4, 5, 6, 7, 8, 9).

Число в десятичной системе счисления записывается в виде суммы числового ряда степеней основания (в данном случае 10), в качестве коэффициентов которых выступают цифры данного числа.

Пример:

765,34510=7⋅102+6⋅101+5⋅100+3⋅10−1+4⋅10−2+5⋅10−3

Двоичная система счисления

Основание: p=2.

Алфавит: 0,1.

Двоичную систему счисления широко применяют в вычислительной технике. К ее достоинствам относятся:

- возможность использования наиболее простой элементной базы микроэлектроники - всего с двумя устойчивыми состояниями;

- возможность использования аппарата булевой алгебры для выполнения логических преобразований информации;

- возможность использования простейших правил арифметики.

Основной недостаток двоичной системы - быстрый рост количества разрядов, необходимых для записи чисел. По этой, а также по некоторым другим причинам в вычислительной технике, кроме двоичной, применяются также восьмеричная и шестнадцатеричная системы счисления.

Число в двоичной системе счисления записывается в виде суммы числового ряда степеней основания (в данном случае 2), в качестве коэффициентов которых выступают цифры данного числа.

Пример:1011,012=1⋅23+0⋅22+1⋅21+1⋅20+0⋅2−1+1⋅2−2

Восьмеричная система счисления

Основание: p=8.

Алфавит: 0,1,2,3,4,5,6,7.

Восьмеричная система чаще всего используется в областях, связанных с цифровыми устройствами. Характеризуется лёгким переводом восьмеричных чисел в двоичные и обратно, путём замены восьмеричных чисел на триады (группы по 3 разряда) двоичных. Ранее широко использовалась в программировании и вообще компьютерной документации, однако в настоящее время почти полностью вытеснена шестнадцатеричной.

Число в восьмеричной системе счисления записывается в виде суммы числового ряда степеней основания (в данном случае 8), в качестве коэффициентов которых выступают цифры данного числа.

Пример:567,128=5⋅82+6⋅81+7⋅80+1⋅8−1+2⋅8−2

Шестнадцатеричная система счисления

Основание: p=16.

Алфавит: 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F.

Здесь только десять цифр из шестнадцати имеют общепринятое обозначение 0,1,...,9. Для записи остальных цифр (10,11,12,13,14 и 15) обычно используются первые шесть букв латинского алфавита.

Шестнадцатеричная система счисления, на сегодняшний день является наиболее популярным средством компактной записи двоичных чисел. Очень широко используется при разработке и проектировании цифровой техники.

Число в шестнадцатеричной системе счисления записывается в виде суммы числового ряда степеней основания (в данном случае 16), в качестве коэффициентов которых выступают цифры данного числа.

Пример:10FC16=1⋅163+0⋅162+F⋅161+C⋅160

Помимо рассмотренных выше позиционных систем счисления, существуют и другие, например:

- троичная (0,1,2);

- пятеричная (0,1,2,3,4)

- двенадцатеричная (0,1,2,3,4,5,6,7,8,9,A,B)

- тринадцатеричная (0,1,2,3,4,5,6,7,8,9,A,B,C).

Наряду с двоичной системой счисления в компьютере используются еще две - восьмеричная и шестнадцатеричная. Восьмеричную и шестнадцатеричную системы называют родственными двоичной, поскольку их основания являются степенями числа 2. Родственными, к примеру, являются системы с

основаниями 3 и 9.

Перевод чисел внутри родственных систем (в частности, с основаниями 2, 8 и

16) упрощен, поскольку все цифры алфавита для систем с большим основанием можно представить совокупностью цифр системы с наименьшим основанием.

Для этого удобно использовать таблицу соотношений чисел в системах счисления с основаниями 10, 2, 8 и 16:

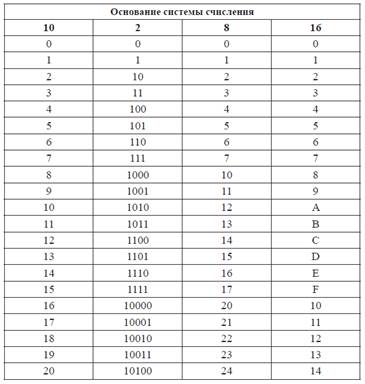
Из таблицы видно, что все восьмеричные цифры (от 0 до 7) можно записать при помощи трех двоичных разрядов. На этом основан быстрый перевод из восьмеричной системы в двоичную и наоборот.

Для перевода восьмеричного числа в двоичное достаточно каждую цифру этого числа заменить двоичной триадой (три разряда) в соответствии с таблицей (если нужно, слева дописывается дополнительный ноль).

Пример:734,468=111011100,1001102

Для перевода двоичного числа в восьмеричное следует воспользоваться следующим алгоритмом:

- разделить целую часть числа на триады от младших разрядов к старшим (влево от запятой);

- разделить дробную часть на триады в обратном направлении (вправо от запятой);

- заменить каждую триаду двоичных чисел соответствующей восьмеричной цифрой по таблице, предложенной выше;

- недостающие до триады позиции заполнить незначащими нуями.

Пример:1010,111112=001010,1111102=12,768

Подобным свойством обладают и шестнадцатеричные цифры. Все шестнадцатеричные цифры (от 0 до F)

можно записать при помощи четырех двоичных разрядов (тетрады) (см. таблицу выше).

Пример:A0,F816=10100000,11111000210101001,101112=10101001,101110002=A9, B816

Поразрядные способы перевода чисел можно использовать для сокращения действий при переводе числа, например, из десятичной системы в двоичную. Для этого целое число делением (дробное - умножением) сначала переводят в восьмеричную систему, а затем из восьмеричной системы поразрядно в двоичную систему.

Если в качестве промежуточной системы использовать двоичную, то существенно упрощается перевод из восьмеричной системы в шестнадцатеричную и обратно. Это показано в следующем примере.

Пример:Дано: A8=275,034. НайтиA16

Решение:A8=275,034 A2=010111101,000011100

A2=10111101,00001110 A16=BD,0E

Ответ: A16=BD,0E

3. Способы измерения информации. Единицы измерения информации.

При работе на компьютере информация понимается как данные, и должна быть представлена в форме, которую машина может воспринимать и обрабатывать.

Данные (data) – зафиксированные наблюдения, которые в данный момент времени не оказывают воздействия на управление.

Данные обычно представлены в форме, которая позволяет ее использовать для компьютерной обработки и передачи, то есть, закодированы, могут храниться.

Информацией является содержание, значение данных, или факты, которые используются для принятия решения.

В информатике используются различные подходы к измерению информации:

Содержательный подход к измерению информации. Сообщение – информативный поток, который в процессе передачи информации поступает к приемнику. Сообщение несет информацию для человека, если содержащиеся в нем сведения являются для него новыми и понятными Информация - знания человека ? сообщение должно быть информативно. Если сообщение не информативно, то количество информации с точки зрения человека = 0. (Пример: вузовский учебник по высшей математике содержит знания, но они не доступны 1-класснику)

Алфавитный подход к измерению информации не связывает кол-во информации с содержанием сообщения. Алфавитный подход - объективный подход к измерению информации. Он удобен при использовании технических средств работы с информацией, т.к. не зависит от содержания сообщения. Кол-во информации зависит от объема текста и мощности алфавита. Ограничений на max мощность алфавита нет, но есть достаточный алфавит мощностью 256 символов. Этот алфавит используется для представления текстов в компьютере. Поскольку 256=28, то 1символ несет в тексте 8 бит информации.

Вероятностный подход к измерения информации. Все события происходят с различной вероятностью, но зависимость между вероятностью событий и количеством информации, полученной при совершении того или иного события можно выразить формулой которую в 1948 году предложил Шеннон.

Количество информации - это мера уменьшения неопределенности.

1 БИТ – такое кол-во информации, которое содержит сообщение, уменьшающее неопределенность знаний в два раза. БИТ- это аименьшая единица измерения информации

Единицы измерения информации: 1байт = 8 бит

1Кб (килобайт) = 210 байт = 1024 байт

1Мб (мегабайт) = 210 Кб = 1024 Кб

1Гб (гигабайт) = 210 Мб = 1024 Мб