Решение СЛУ установившегося режима методом Зейделя
Линейные уравнения установившегося режима получаем при задании в узлах нагрузки или генерации в виде постоянного тока:
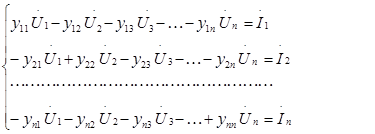 (1)
(1)
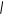 Для решения системы (1) методом Зейделя, ее нужно преобразовать: каж-дое уравнение системы решить относительно одной из неизвестных величин, при этом мы предполагаем, что yij≠0.
Для решения системы (1) методом Зейделя, ее нужно преобразовать: каж-дое уравнение системы решить относительно одной из неизвестных величин, при этом мы предполагаем, что yij≠0.
Решаем 1-е уравнение относительно 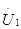 :
:
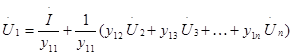
Решаем 2-е уравнение относительно 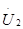 и т.д.
и т.д.
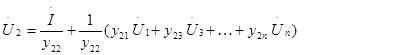 (2)
(2)
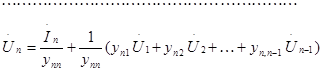
Введем обозначения:
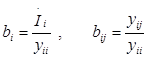 , i, j = 1, 2,..., n; i≠j.
, i, j = 1, 2,..., n; i≠j.
С учетом этих обозначений систему (2) можно записать в более простом виде:
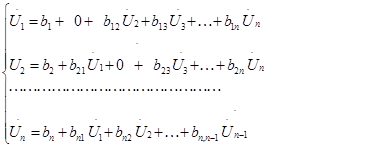 (3)
(3)
Зададим начальные значения неизвестных U1(0),U2(0),…,Un(o), подставим их в правую часть системы (2) или (3), выполним вычисления и определим первое приближение неизвестных U1(1),U2(1),…,Un(1), снова подставим их в правую часть (2) или (3) и определяем следующие приближение неизвестных и т. д. Такой алгоритм соответствует методу простой итерации.
Метод Зейделя является модификацией метода простой итерации. Суть его в следующем: найденное на текущей (к+1) итерации приближение напряжения узла с номером (i-1), то есть 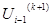 , сразу используется для вы-числения (к+1) приближения напряжения следующего узла с номером i, то есть
, сразу используется для вы-числения (к+1) приближения напряжения следующего узла с номером i, то есть 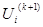 .
.
С учетом этого, итерационный процесс метода Зейделя описывается вы-ажениями, полученными из системы (3):
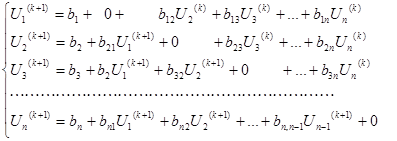 (4)
(4)
То есть полученное (к+1) приближение напряжения 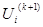 сразу же используется для вычислений (к+1) приближений:
сразу же используется для вычислений (к+1) приближений: 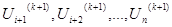
Одно i-ое уравнение системы (4) для вычисления (к+1) приближения напряжения Ui в общем виде можно записать:
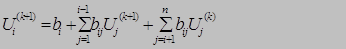 (5)
(5)
В выражении выделяются две группы слагаемых под знаком суммы. В пер-вую входят (к+1)-е приближения неизвестных для узлов с номерами от 1 до (i-1)-го. Во вторую – к-е приближения для узлов с номерами, большими і-го, т.е. от (і+1) до n.
| |

| |
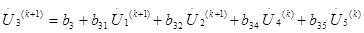
| | | ||||
Общий алгоритм решения систем линейных уравнений методом Зейделя
1. Задание начальных приближений неизвестных. В качестве начальных приближений используются, как правило, номинальные напряжения узлов:
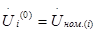 .
.
2. Задание точности расчета Е, предельного количества итераций nпред и других условий расчета.
3. Выполнение итерации по методу Зейделя в соответствии с системой (4):
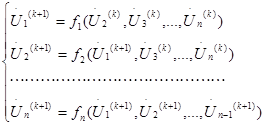
4. Контроль завершения итерационного процесса
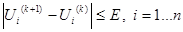
 Если условие не выполняется, то возврат к пункту (3). Расчет повторя-ется при новых (к+1)-х приближениях неизвестных.
Если условие не выполняется, то возврат к пункту (3). Расчет повторя-ется при новых (к+1)-х приближениях неизвестных.
Дата добавления: 2016-01-26; просмотров: 548;
