Обращение матрицы коэффициентов системы уравнений установившегося режима
Ранее рассмотренные методы решения СЛАУ позволяют определить ре-шение системы, записанной в виде
Ax=B => 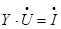 . (1)
. (1)
Часто требуется многократное решение систем уравнений установив-шегося режима при неизменной схеме электрической сети и её параметров и различных наборах заданных значений токов в узлах. Это означает, что мат-рица проводимостей Y остается неизменной, а изменяющимися являются зна-чения вектора свободных членов I. В этом случае решение системы уравне-ний (1) целесообразно искать в виде
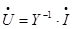 , (2)
, (2)
то есть матрица проводимостей обращается один раз, а решение системы уравнений при изменяющихся значениях элементов вектора І сводится к многократному умножению матрицы Y-1 на новый вектор I.
Обращение матрицы проводимостей требует большого объема вычисле-ний. Существует различные методы обращения матрицы.
Обращение матриц методом упорядоченного исключения неизвестных
В соответствии с определением обратной матрицы - прямая матрица А, будучи умноженной на обратную матрицу А-1, дает единичную матрицу Е, можно записать:
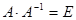 .
.
Если исходная матрица : 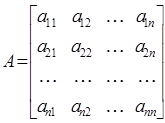 ,
,
искомая обратная матрица: 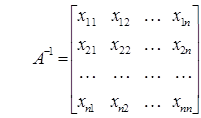 ,
,
тогда их произведение:
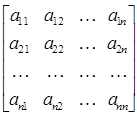
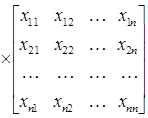
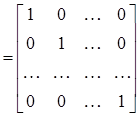
Перемножая строки матрицы А поочередно на столбцы матрицы А-1, получаем n систем линейных уравнений, в каждой из которых в правой части будут элементы соответствующего столбца единичной матрицы, а неизвест-ными – элементы соответствующего столбца обратной матрицы.
При умножении первой строки матрицы А на первый столбец матрицы А-1, получаем в правой части первый элемент 1-го столбца единичной матри-цы. Он равен 1. Умножив вторую строку матрицы А на 1-й столбец матрицы А-1 получаем 2 –й элемент 1 – го столбца единичной матрицы (он равен 0) и т.д. Перемножив все n строк исходной матрицы А на 1- й столбец матрицы А-1, получаем систему уравнений, в правой части которой – элементы 1–го столбца единичной матрицы, неизвестные – элементы 1–го столбца обрат-ной матрицы xі1 ( і = 1, ... n ):
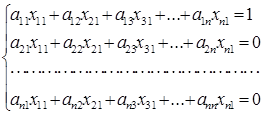
Решив эту систему уравнений, определим элементы первого столбца ис-комой обратной матрицы.
Вторую систему уравнений получим умножением матрицы А на второй столбец обратной матрицы. В полученной системе уравнений: в правой части – элементы 2–го столбца единичной матрицы, неизвестные – 2–й стол-бец обратной матрицы xi2 ( I = 1, … ,n):
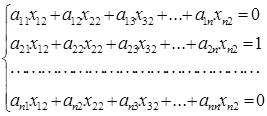
Решив эту систему уравнений, найдем элементы второго столбца обрат-ной матрицы.
Перемножаем т.о. матрицу А на остальные столбцы матрицы А-1. При умножении на последний столбец , получаем систему уравнений и решаем её:
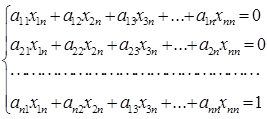
В результате получили n независимых систем линейных уравнений с n неизвестными (элементы столбцов искомой обратной матрицы). Каждая система состоит из n уравнений. Решая их любым из известных методов, определим элементы обратной матрицы.
Метод прост алгоритмически, но требует большого объёма вычислений.
Решение систем линейных уравнений методом двойной фактори-
Зации
Решение ищем в виде: 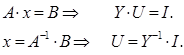
Двойная факторизация - представление обратной матрицы в виде про-изведения элементарных верхних и нижних треугольных матриц, в которых не равны нулю элементы только одной строки или одного столбца. Такие матрицы называются факторными.
Произведение факторных матриц дает обратную матрицу.
Рассмотрим структуру факторных матриц:
1) Левая факторная матрица на к-м шаге факторизации Lk.
| |
|

|
|
i
| 1 | ||||
| 1 | ||||
| Lkk | ||||
| … | 1 | |||
| Lnk | 1 |
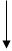
| |
|
|
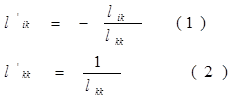
2) Правая факторная матрица Rк.
|
| |||||
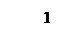 | ||||||
| 1 | ||||
| 1 | ||||
| 1 | rr,k+1 | ...rk,n | ||
| 1 | ||||
| 1 |
| |
В к-ой строке элементы, лежащие правее диаго-нали, не равны нулю. Все остальные элементы матрицы
|
Таких матриц может быть n-1. Элементы мат-рицы R вычисляются по формуле:
|
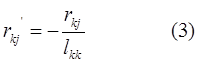
k=1…n, j=k+1…n, i=k+1…n.
|
Для квадратной матрицы А размерностью  существует n левых и (n-1) правых факторных матриц, таких, что их произведение дает обратную мат-рицу:
существует n левых и (n-1) правых факторных матриц, таких, что их произведение дает обратную мат-рицу:
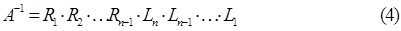
Здесь: А – исходная матрица; L – левые факторные матрицы, полученные на 1, 2, …, n шагах факторизации; R – правые факторные матрицы.
Существует эффективные алгоритмы перемножения факторных матриц, в которых нулевые элементы и единицы на диагонали не хранятся, а подразу-меваются в ходе вычислений. В памяти хранятся и участвуют в вычислениях только значащие элементы матриц.
Алгоритм факторизации:
1) Выбор очередного ведущего элемента акк, определяющего опорную
строку и опорный столбец;
2) На основе элементов опорной строки и опорного столбца
пересчитываются все остальные элементы матрицы по формуле:
| ||||||||
| к |
|
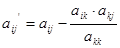 (5)
(5)
3) Пересчитываем элементы опорного столбца
по формуле (1);
4) Пересчитываем элементы опорной строки по
формуле (3);
5) Пересчитываем ведущий элемент по формуле (2)
L1 … Lк … Ln
|
6) Если таким образом получены n левых и (n-1) правая факторная мат-рица, то переходим к пункту 7, иначе - возврат к пункту 1;
В результате все поле матрицы будет заполнено элементами факторных мат-риц L и R. Полученная матрица называется факторизованной;
7) Расчет обратной матрицы А-1 перемножением факторных матриц по формуле (4);
8) Решение системы уравнений по формуле: 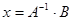 .
.
Примечания:
1. Метод использует простые преобразования;
1.2. Объем занимаемой памяти ЭВМ зависит от степени разрежен-ности матрицы и последовательности выбора ведущих элемен-тов;
1.3. Возможность реализации серии расчётов режимов при меняющихся значениях элементов вектора І и неизменной матрице проводимостей Y.
Примеры:
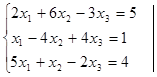 Решение системы:
Решение системы: 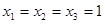
Решаем СЛАУ методом Гаусса. Прямой ход – 2 шага исключения неиз-вестных:
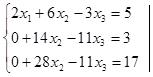 1-й шаг
1-й шаг
Умножаем 2-е уравнение на -2 и складываем его с 1-м. При этом исключается х1 из 2-го уравнения.
Умножаем 1-е уравнение на 5, а 3-е на -2 и складываем их. Исключается х1 из 3-го уравнения.
2-й шаг
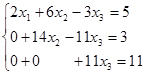
Умножаем 2-е уравнение на -2 и складываем его
с 3-м. При этом исключается х2 из 3-го уравне- ния.
Получили эквивалентную систему уравнений с треугольной матрицей коэффициентов.
Обратный ход:
Из последнего уравнения находим х3. Подставляем его во 2-е уравнение и из него находим х2. Подставляем х2 и х3 в 1-е уравнение и определяем х1.
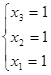 Для проверки подставляем х1 ,х2, х3 в исходную систему.
Для проверки подставляем х1 ,х2, х3 в исходную систему.
Решаем СЛАУ методом Жордана
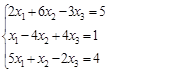 Нужно выполнить 3 шага исключения неизвестных.
Нужно выполнить 3 шага исключения неизвестных.
В результате их исходная прямоугольная матрица коэффициентов преоб-разуется в единичную.
1-й шаг. Делим 1-е уравнение на коэффициент при х1, т.е. 2. и исключаем х1 из уравнений 2 и 3. Получаем эквивалентную СЛАУ:
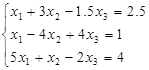 =>
=> 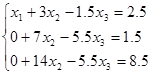
2-й шаг. Делим 2-е уравнение на коэффициент при х2 , т.е. 7 и исключаем х2 из уравнений 1 и 3. Получаем эквивалентную систему:
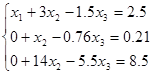 =>
=> 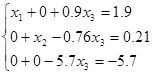
3-й шаг. Делим 3-е уравнение на коэффициент при х3 , т.е. -5.7 и исклю-чаем неизвестную х3 из уравнений 1 и 2. Получаем эквивалентную систе-му уравнений с единичной матрицей коэффициентов:
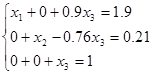 =>
=> 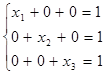 Результат решения СЛАУ очевиден: х1 = х2 = х3 =1.
Результат решения СЛАУ очевиден: х1 = х2 = х3 =1.
Т.е. искомые значения неизвестных равны правым частям уравнений сис-темы, полученным после n-го шага исключения неизвестных.
Решаем СЛАУ методом LU - факторизации
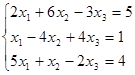
Для разложения матрицы коэффициентов на две треугольные – реализуем алгоритм Краута.
Выбираем опорный элемент. Он равен 2. Делим на него элементы опорной (1-й) строки. Опорный столбец (1-й) оставляем без изменений. Пересчитываем остальные элементы матрицы. Это 1-й шаг факторизации.


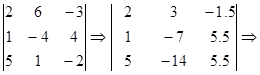
Снова выбираем опорный элемент. Он равен -7. Делим на него элемент опорной (2-й) строки. Опорный столбец (2-й) оставляем без изменений. Пересчитываем остальные элементы матрицы. Это 2-й шаг факторизации.



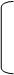
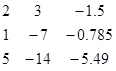
Из полученной матрицы выделяем нижнюю треугольную матрицу L (включающую и диагональные элементы) и верхнюю треугольную матрицу U (с единицами на диагонали). Их перемножение дает исходную матрицу коэффициентов.
|
|
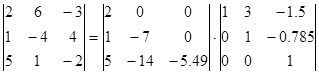
Составляем 2 вспомогательные системы уравнений с использованием этих треугольных матриц:
LY=B ; Ux=Y , или
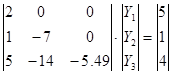 Y1=2.5; Решаем эту систему и находим
Y1=2.5; Решаем эту систему и находим
Y1-7Y2=1; значения Y .
Y2= 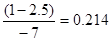
5Y1-14Y2-5.49Y3=4
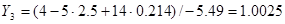
Подставляем их значения во вторую систему, решаем её и определяем искомые значения Х :
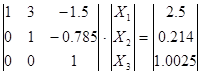 X3=1.0025; X2=1.0009; X1=1.00087
X3=1.0025; X2=1.0009; X1=1.00087
Для проверки – подставляем их исходную систему уравнений.
Решаем СЛАУ методом двойной факторизации
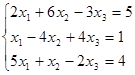
Определяем обратную матрицу коэффициентов. 1-й шаг факторизации:
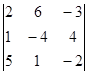 Выбираем ведущий элемент – он равен 2. Ведущие строка и
Выбираем ведущий элемент – он равен 2. Ведущие строка и
столбец – 1-я строка и 1-й столбец.
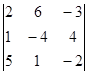 Выбираем
Выбираем
ведущий элемент он равен 2. Ведущие строки и столбец -1-я строка и 1-й столбе
Пересчитываем элементы, не входящие в опорную строку и столбец по формуле (1) (- аналогично алгоритму Краута):
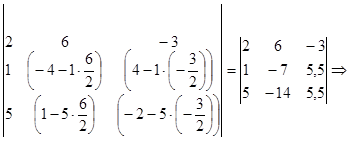
Пересчитываем по формулам (1) и (3) элементы ведущего столбца и строки, т.е. делим их на ведущий элемент:
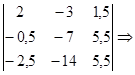
Пересчитываем ведущий элемент по формуле (2):
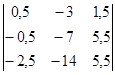
В полученной матрице выделяем элементы первой левой (L1) и первой правой (R1) факторных матриц.
2-й шаг факторизации:
Выбираем очередной ведущий элемент. Он равен -7. Ведущая строка и столбец – 2-й.
Пересчитываем элем6енты, не входящие входивший в ведущие строки и столбцы:
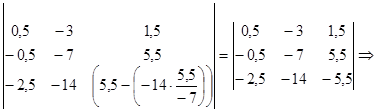
Пересчитываем элементы ведущего столбца и строки:
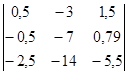
Пересчитываем ведущий элемент:
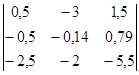
В полученной матрице выделяем элементы очередных левой (L2) и правой (R2) факторных матриц.
3-й шаг факторизации:
Выбираем ведущий элемент. Это -5,5. Пересчитываем его по формуле (2). Получаем факторизованную матрицу: 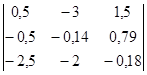 .
.
Её элементы – это элементы всех факторных матриц. Выделяем факторные матрицы.
Обратная матрица определяется:
R1 R2 L3 L2 L1
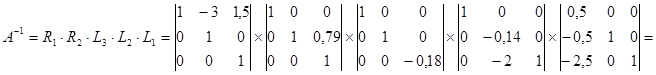
R1∙R2 L3 L2 L1 R1∙R2∙L3 L2
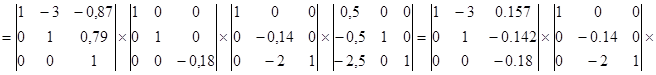
L1 R1∙R2∙L3∙L2 L1 A-1
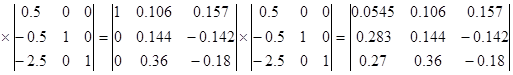
Для проверки – перемножим исходную и обратную матрицы: А∙А-1
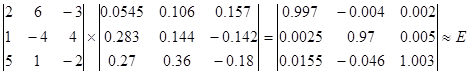
Решаем систему уравнений:
X=A-1∙B
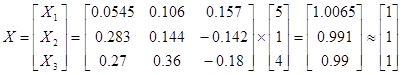
Дата добавления: 2016-01-26; просмотров: 893;
